
지난번의 후속편

히스토그램: 계급 수 결정 방법
기준은 있지만 결정적인 것은 없다. 최대값과 최소값, 데이터 범위, 데이터 수 등을 참고한다.
스타제스 공식
계급의 수 = 1 + log₂n
엑셀에서 계산하기
셀: = log ( C13 , 2 )+1
예: 셀의 C13에 데이터 수가 들어있는 경우
정규분포에 가까운 히스토그램을 만드는 것과 같은 계급수를 도출하도록 계산합니다.

히스토그램: 3단계
1. 미세값(이 경우 G5)을 클릭한 후 Ctrl + C 키를 눌러 복사한다.
2. 붙여넣을 셀 범위 'F7:F13'을 드래그한다.
3. 홈 탭의 '붙여넣기' - > '형식 선택 후 붙여넣기'를 클릭한다.
4. '값'과 '빼기'를 클릭하고 OK 버튼을 클릭한다.

연습문제 4와 5의 답변 예시

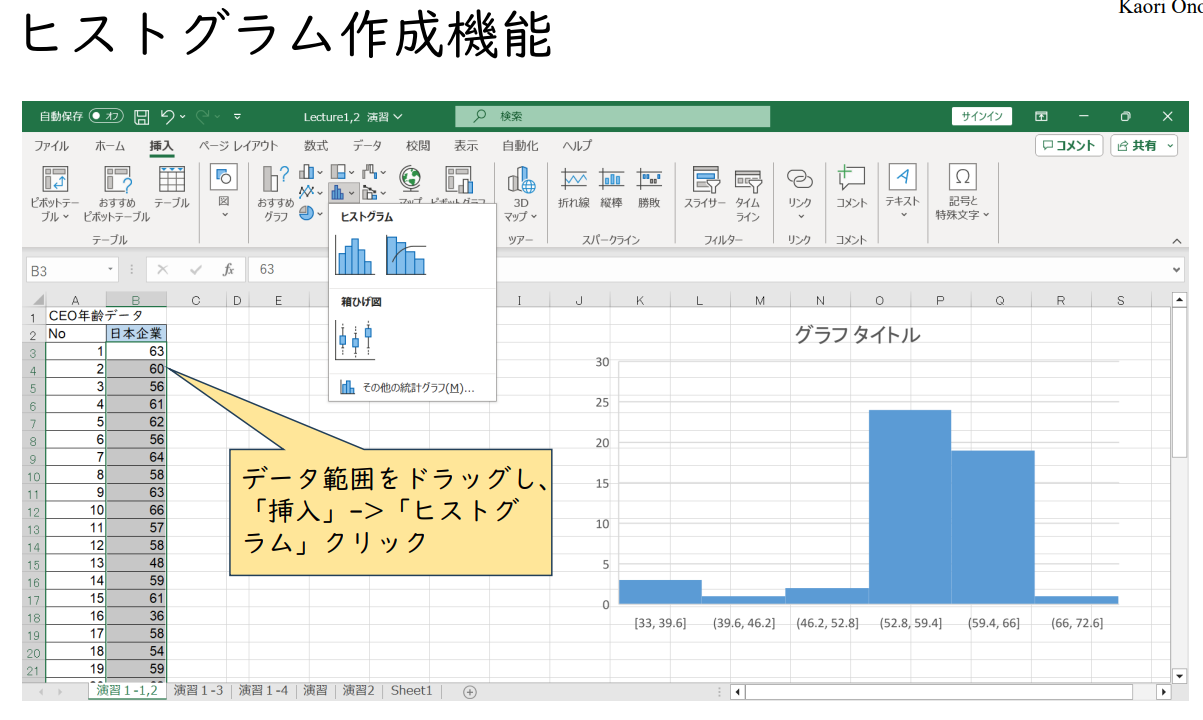
히스토그램 생성 기능
데이터 범위를 드래그하여 "삽입" -> "히스토그램"을 클릭합니다.
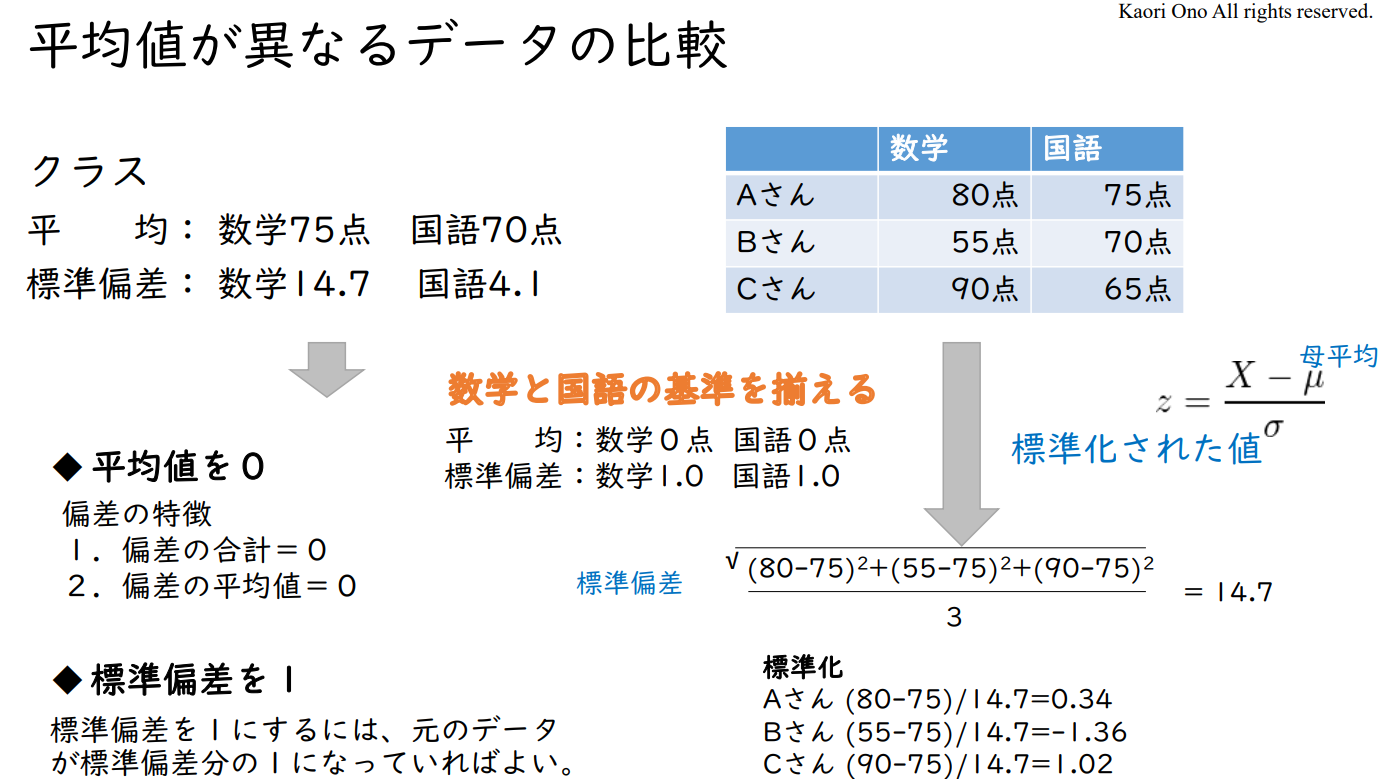
평균값이 다른 데이터 비교
◆ 평균값을 0
편차의 특징
1. 편차의 합계 = 0
2. 편차의 평균값 = 0
◆ 표준편차를 1
표준편차를 1로 하려면 원래 데이터가 표준편차만큼의 1이면 된다.
| 구분 | 점수 | 평균 | 표준편차 | 표준화값 | 점수를 표준편차로 나눈 값 |
| A | 80 | 75 | 14.72 | 74.90 | 5.43 |
| B | 55 | 75 | 14.72 | 49.90 | 3.74 |
| C | 90 | 75 | 14.72 | 84.90 | 6.11 |
| 평균 | 75 | 69.90 | |||
| 표준편차 | 14.72 | 14.72 | 1.00 |
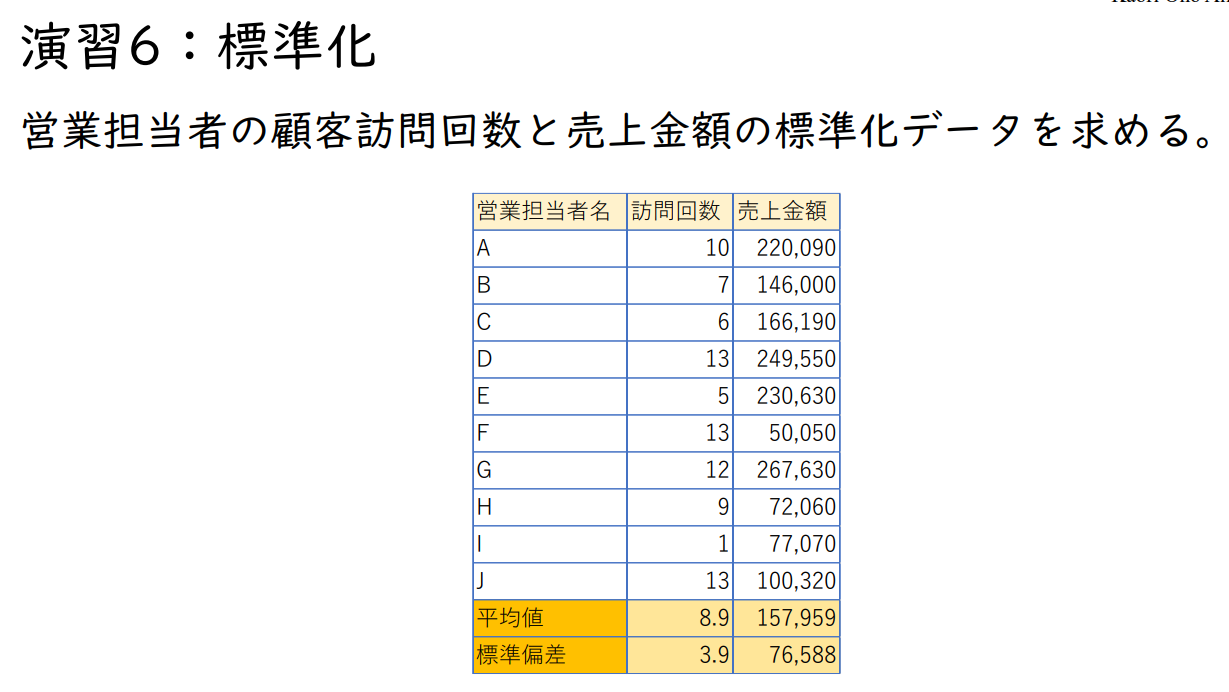
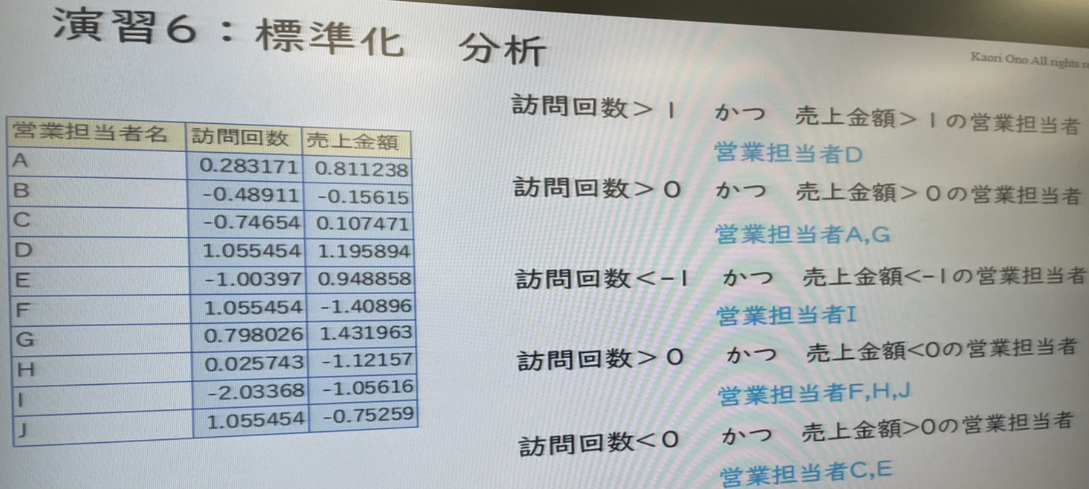
연습 6: 표준화
영업 담당자의 고객 방문 횟수와 매출 금액의 표준화 데이터를 요구한다.
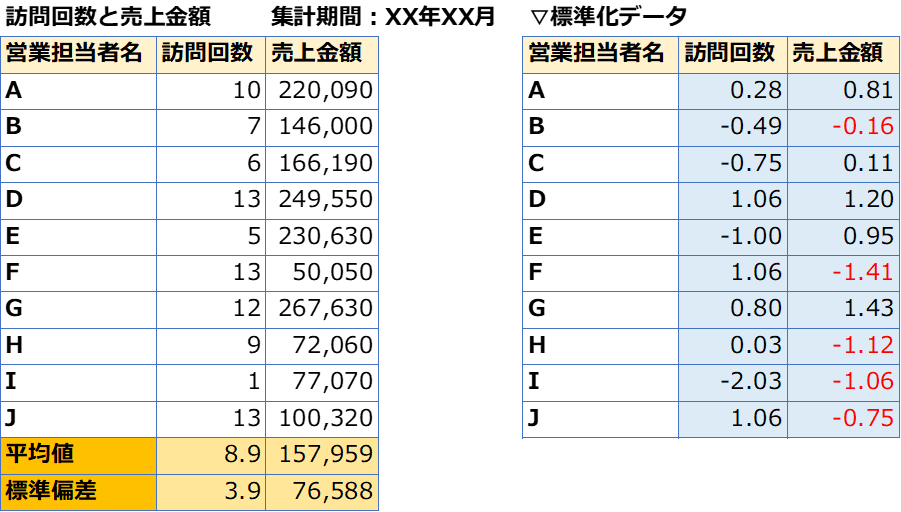
- 방문횟수 > 1 이고 매출액 > 1 인 영업담당자
영업사원 D - 방문횟수 > 0 이고 매출금액 > 0 인 영업담당자
영업사원 A, G - 방문횟수 -1 및 매출금액 -1 인 영업담당자
영업사원 I - 방문횟수 > 0 이고 매출금액이 0 인 영업담당자
영업담당자 F, H, J - 방문횟수 < 0 이고 매출금액 > 0 인 영업담당자
영업담당자 C, E
전체 강의
일부 데이터로 전체 추정하기
정규분포, 표준정규분포
확률
추정과 검정
Q
1. A씨가 시험을 치렀는데, 그 결과 편차가 70이었습니다.
이 시험은 10만 명의 학생이 응시했습니다.
이 때 A 씨보다 성적이 더 좋은 사람은 총 몇 명이나 있었을까요?
2. 구조조정은 기업의 주가에 어떤 영향을 미치는가?
조기 희망퇴직을 모집한다고 발표한 100개 기업의 공시일 기준 주가 변동에 대한 데이터를 입수했다.
수익률의 평균은 -1.4%, 표준오차는 0.7%였다.
'조기 희망퇴직을 모집한 기업의 주가는 하락한다'는 것이 통계적으로 유의미하다고 할 수 있을까?

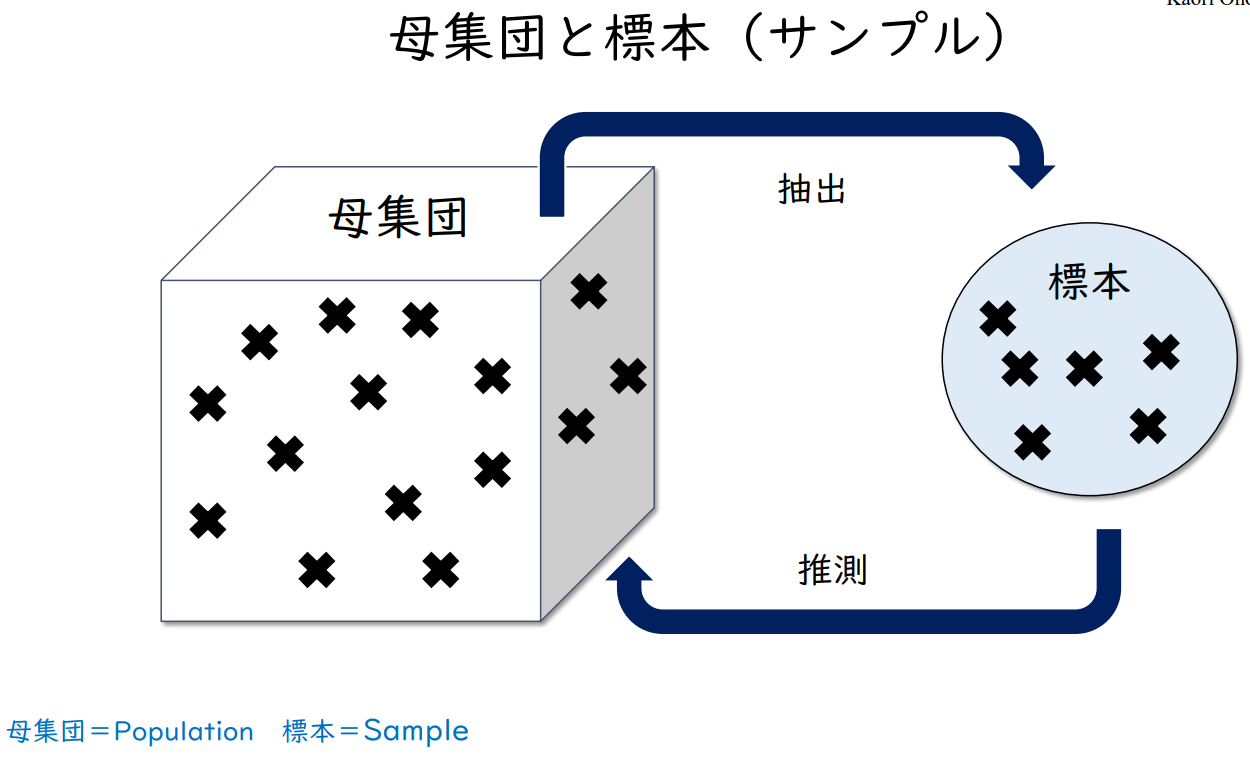
모집단과 표본의 관계

모집단과 표본(샘플)
모집단 = Population, 표본 = Sample
모집단과 표본(샘플)
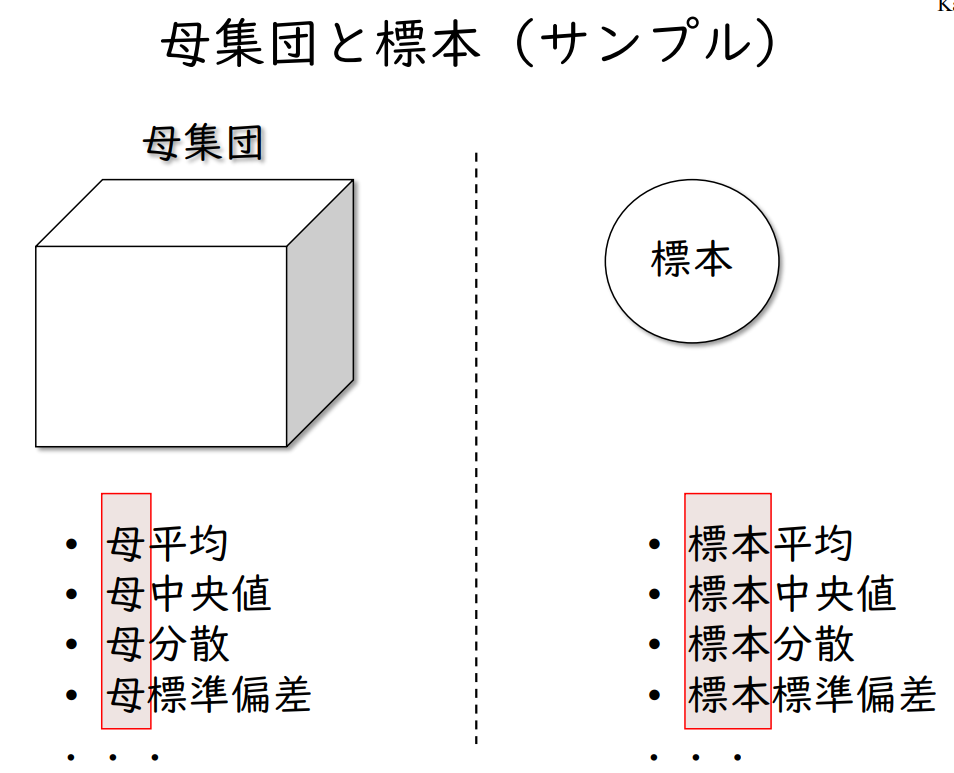
| 모집단 | 표본 |
| - 모 평균 - 모 중앙 - 모 분산 - 모 표준 편차 |
- 표본 평균 - 표본 중심값 - 표본 분산 - 표본 표준편차 |
표본을 선택하는 방법
무작위 추출 (random sampling)
- 임의성 없이
- 편견 없이
- 골고루
무작위 추출 방법
- 단순무작위추출법 : 난수표나 번호표를 뽑아서 필요한 수의 표본을 추출하는 방법
- 계통추출법 : 대상자에게 번호를 부여하여 균등한 간격을 두고 추출
- 다단계 추출법 : 추출단위에서 추출(예: 시군구->읍면동->지구->개인)
- 층화추출법 : 그룹(층) 내 비율로 추출(예: 남녀 비율이 7대 3)
논문
데이터 대상 선정방법에 대한 설명

점추정

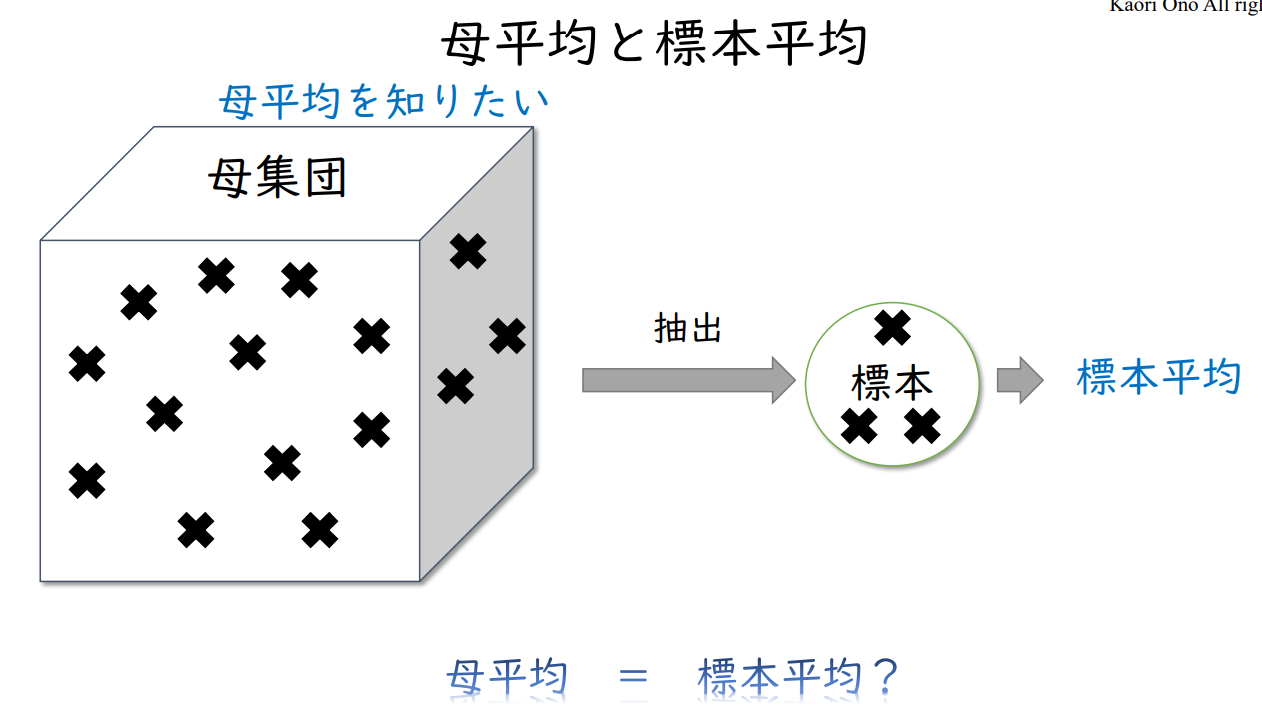
모평균과 표본평균
| 모집단 모평균을 알고 싶다 |
추출 → |
표본 | → | 표본평균 |
모 평균 = 표준 평균?
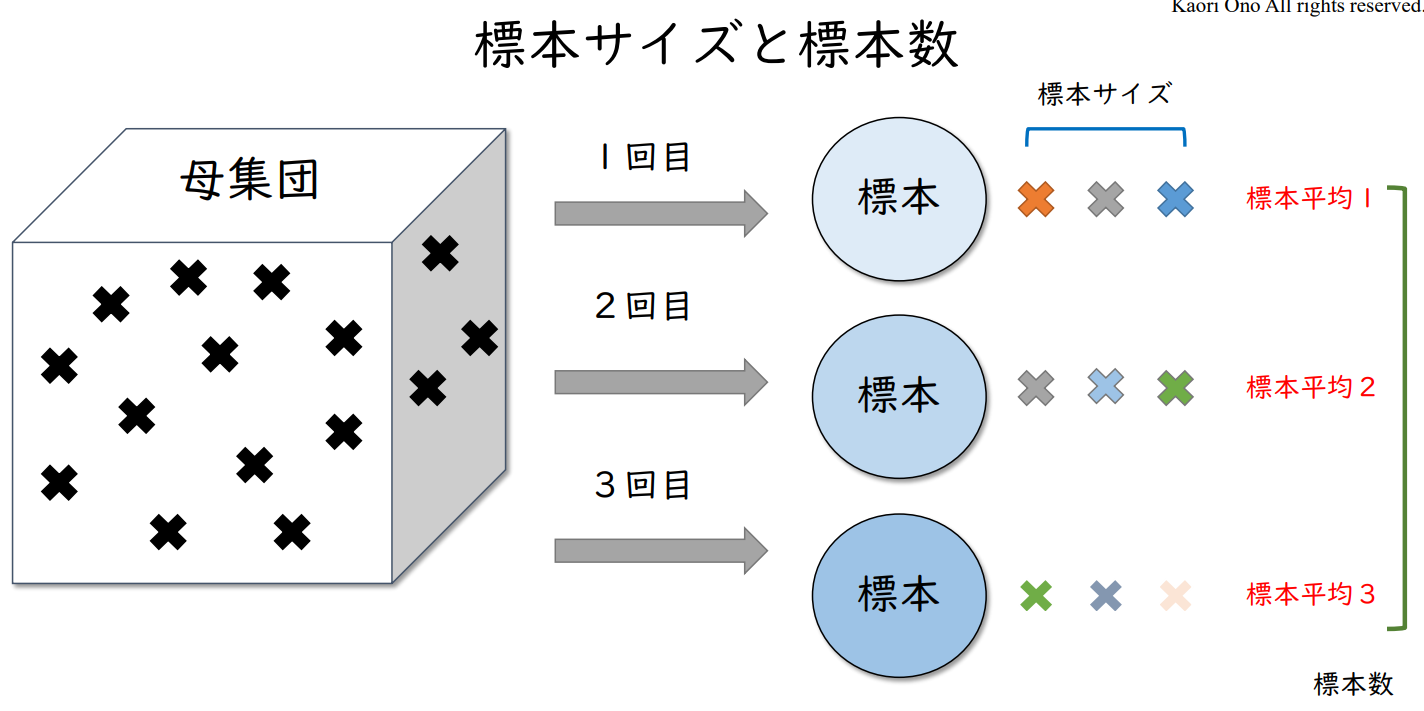
표본 크기 및 표본 수
| 모집단 | 1회차 → |
표본 | 표본사이즈 | 표본평균1 |
| 2회차 → |
표본 | 표본평균2 | ||
| 3회차 → |
표본 | 표본평균3 |
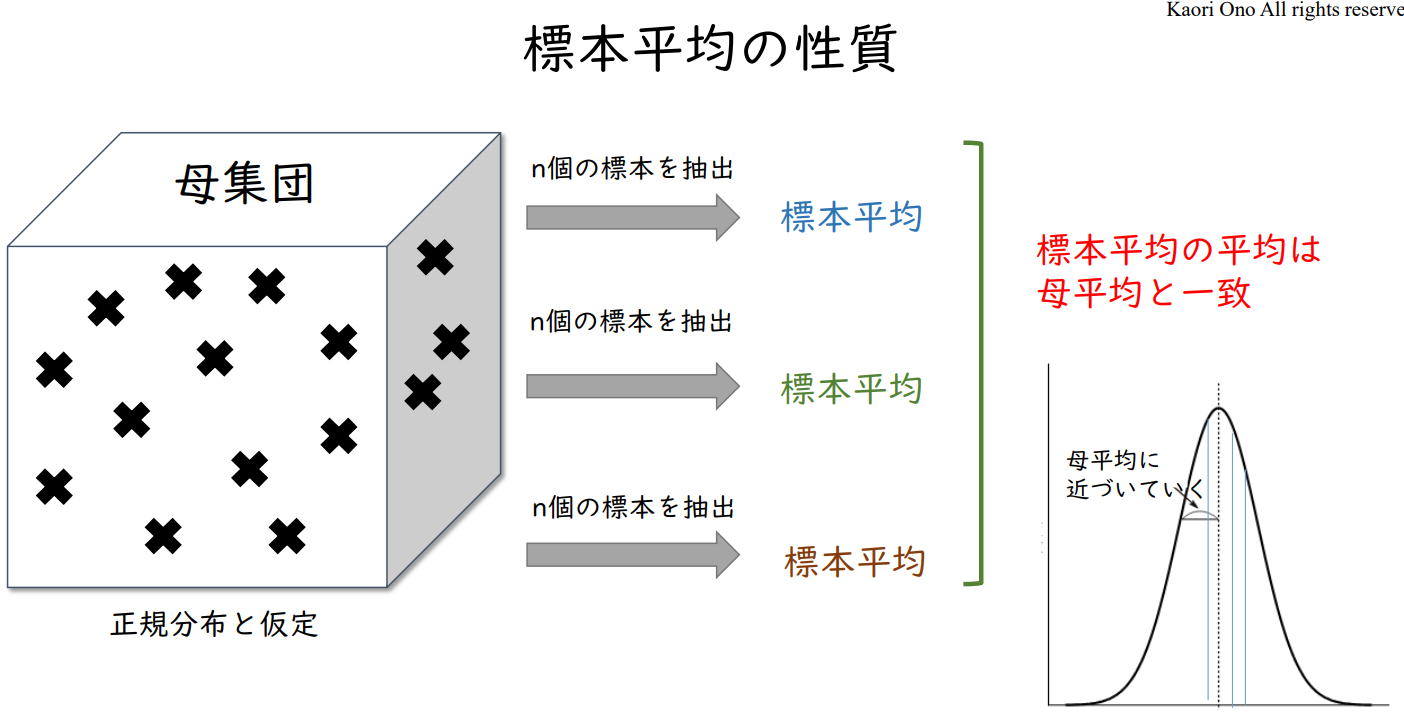
표본 평균의 특성
| 모평균 정규분포를 가정 |
n개의 표본을 추출 → |
표본평균 | 표본평균의 평균은 모평균과 일치 |
| n개의 표본을 추출 → |
표본평균 | ||
| n개의 표본을 추출 → |
표본평균 |
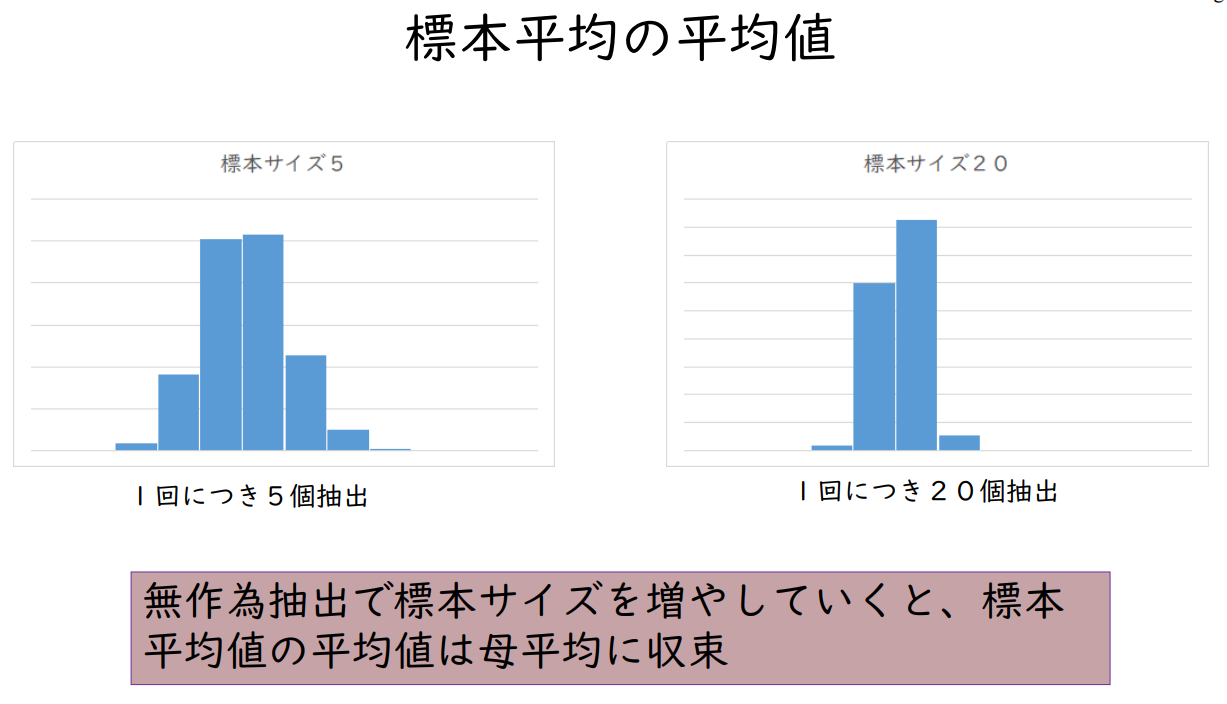
표본 평균의 평균값
| 1회에 5개 추출 | 1회에 20개 추출 |
무작위 추출로 표본 크기를 늘리면 표본 평균값의 평균값은 모평균에 수렴
비편향성(unbiasedness) = 편파적이지 않음
표본이 추정하는 기대값이 실제 모수의 값과 동일하다.
| 모집단 | → | 표본 | 계산된 값 ↓ |
| → | 표본 | ||
| → | 표본 | ||
| 모수 - 모평균 |
= 점추정 |
기대치 - 표본평균 |
← |
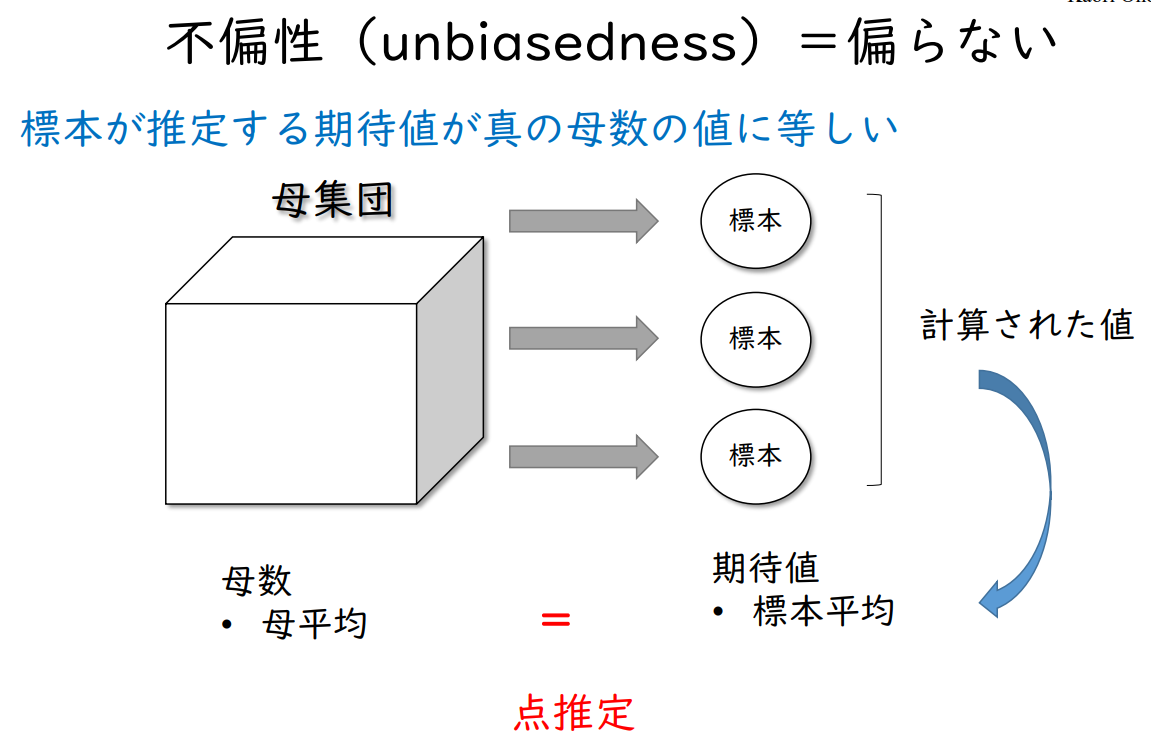
평균점 추정
| 모집단 | 표본추출 → |
A | 170cm | 표본평균 167cm ↓ |
| 표본추출 → |
B | 166cm | ||
| 표본추출 → |
C | 165cm | ||
| 불균형성의 특성으로 인해 표본 평균을 모평균으로 사용할 수 있다. | ← | |||
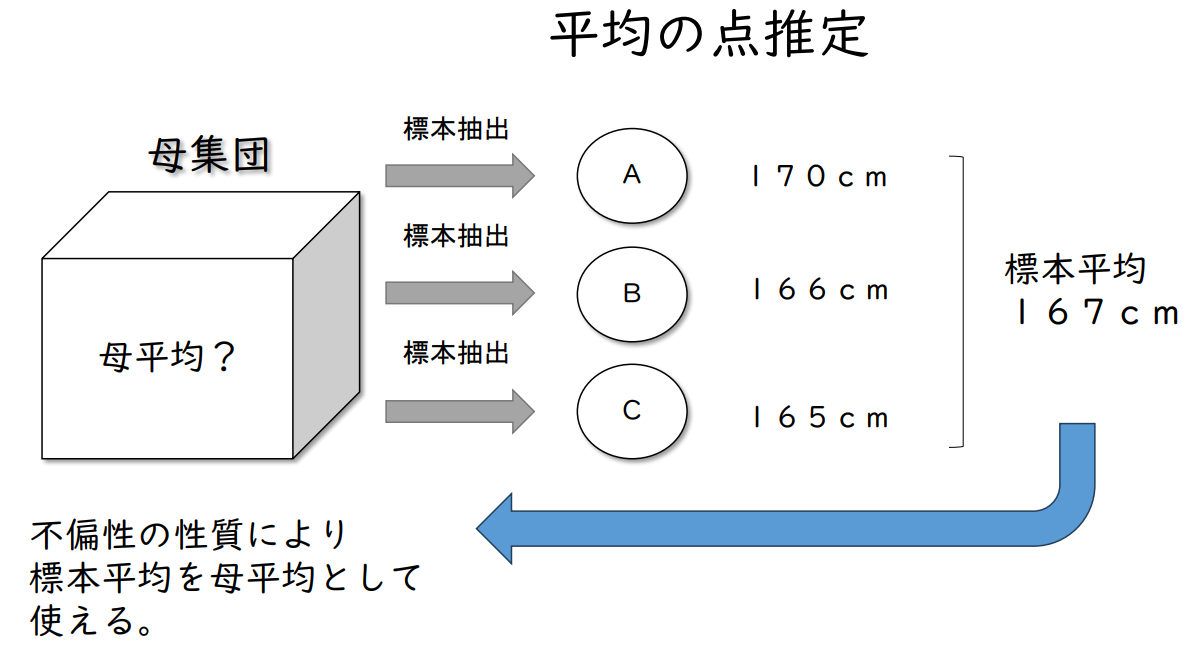
분산점 추정
| 모집단 | 표본추출 → |
A | 170cm | 표본분산 { 3² + (-1)² + (-2)² } / 3 = 4.66 |
| 표본추출 → |
B | 166cm | ||
| 표본추출 → |
C | 165cm | ||
| 표본평균 167cm |
편향성을 이용할 수 없다.
불편분산
{ 3² + (-1)² + (-2)² } / ( 3 - 1 )
= 7
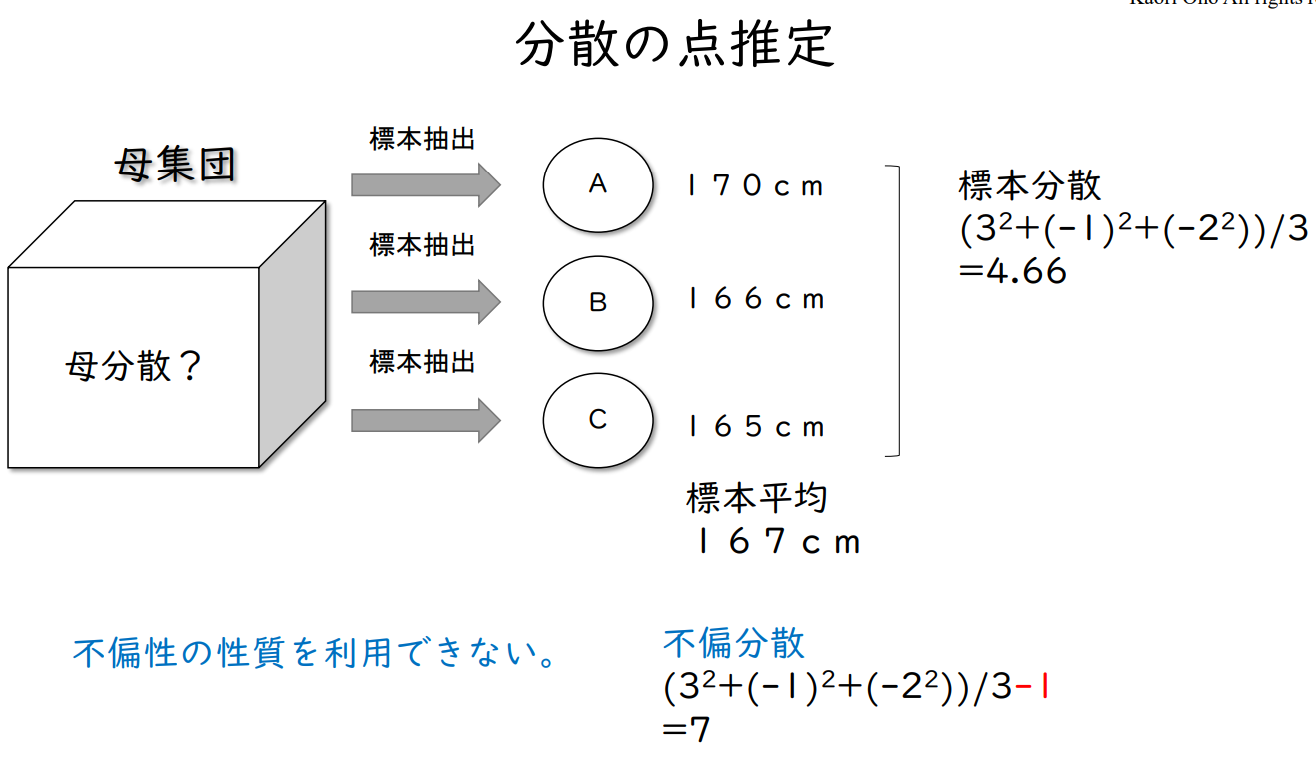
분산은 표본 분산이 아닌 불균형 분산
문제점: 표본분산은 모분산을 작게 추정하게 된다.
| 표본분산 | 표본 평균으로부터의 거리의 제곱의 총합 | |
| 표본의 개수 | ||
| 불편분산 | 표본 평균으로부터의 거리의 제곱의 총합 | |
| 표본의 개수 - 1 | ||
| 보정: 분모를 작게 해준다 | ||
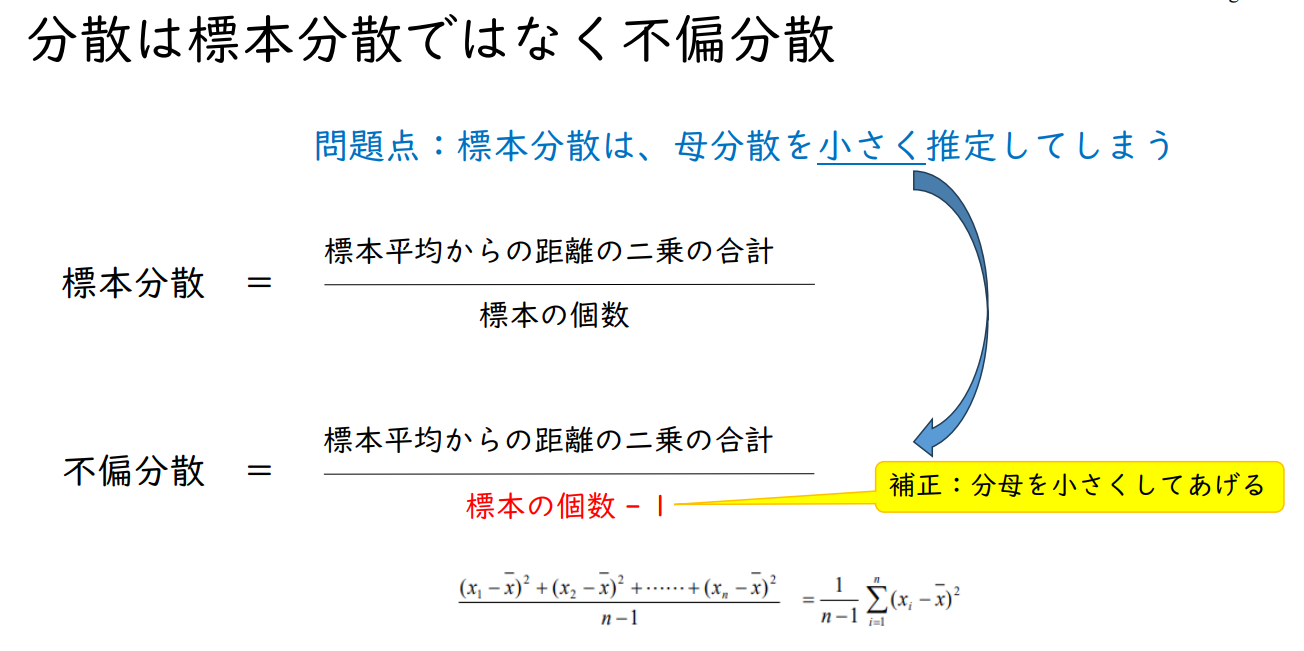
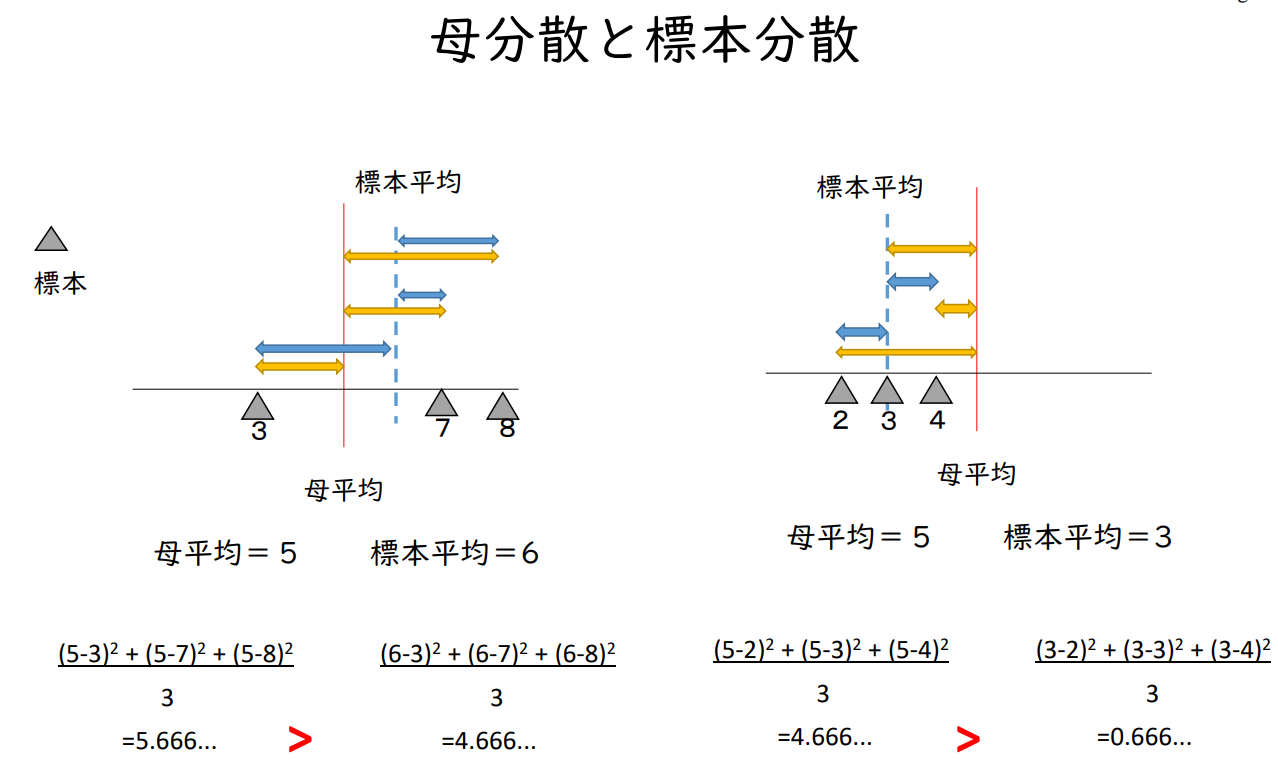
모 분산과 표본 분산
| 모평균 = 5, 표본평균 = 6 | 모평균 = 5, 표본평균 = 3 | ||||
| (5-3)²+(5-7)²+(5-8)² | (6-3)²+(6-7)²+(6-8)² | (5-2)²+(5-3)²+(5-4)² | (3-2)²+(3-3)²+(3-4)² | ||
| 3 | 3 | 3 | 3 | ||
| = 5.666... | > | = 4.666... | = 4.666... | > | = 0.666... |
구간추정

구간추정이란?
- 모집단에서 추출한 표본을 바탕으로 모집단의 값을 구간으로 추정하는 통계학 방법
점 추정 : 표본 평균값➞ "모평균은 XX입니다."
구간 추정 : "모평균은 표본 평균값 ± 00 범위에 있다고 추정한다."
100번 표본을 추출하여 95번은 추정 구간에 들어간다.

확률 변수 (random variable)
주사위 눈의 수의 합계
주사위가 1개
1, 2, 3, 4, 5, 6
발생확률 P(X=k) = 1/6
(k = 1, 2, 3, 4, 5, 6 중 어느 하나)
예. P(X=1) = 1/6, P(X=2) = 1/6
주사위가 2개
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
주사위가 3개
3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18
주사위의 눈의 개수 = 확률 변수 = X
확률로 결정되는 변수

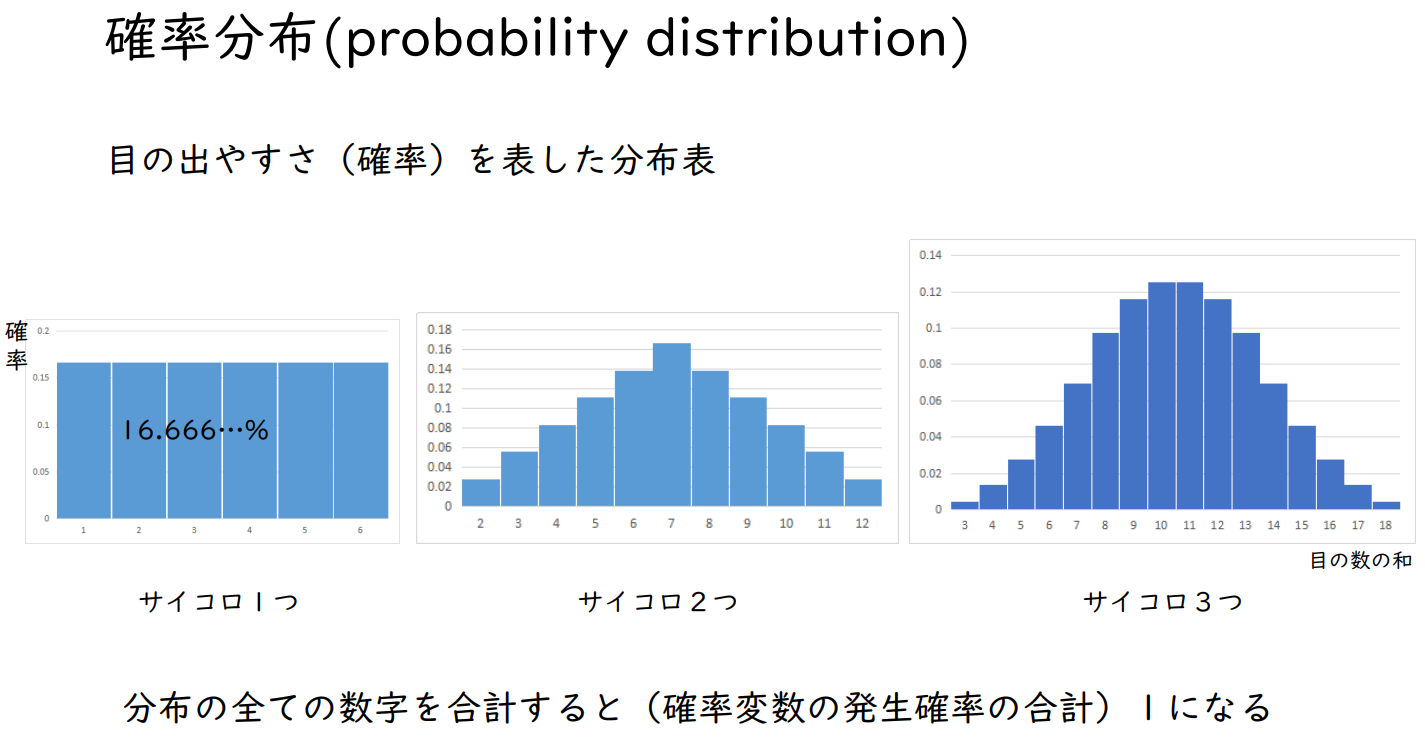
확률 분포(probability distribution)
눈에 띄기 쉬움(확률)을 나타내는 분포표
| 주사위 1개 | 주사위 2개 | 주사위 3개 |
분포의 모든 숫자를 합치면 (확률변수의 발생확률의 합) 1이 된다.
확률 분포의 종류
- 이산형 확률분포 : 수치에 의미가 없고, 확률변수가 연속적이지 않음
예 : 이항분포, 포아송 분포
데이터 예 : 주사위, 동전
설문조사에 의한 남성 = 0, 여성 = 1 - 연속형 확률분포: 수치에 의미가 있고, 확률변수가 연속적이다.
예: 정규분포, 지수분포
데이터 예시 : 키, 체중, 주가 지수 수익률

확률변수의 기대값(Expected value)
어떤 시도의 결과로 얻을 수 있는 수치의 평균값
| 확률변수 X의 기대치를 E(X) | 기대값 E(X) = x₁P₁ + x₂P₂ + x₃P₃ + ... + xₙPₙ |
주사위를 1번 던진 경우
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| P(X) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
확률변수의 기대치
E(X) = 1 x 1/6 + 2 x 1/6 + 3 x 1/6 ... 6 x 1/6
= 21 / 6 = 3.5

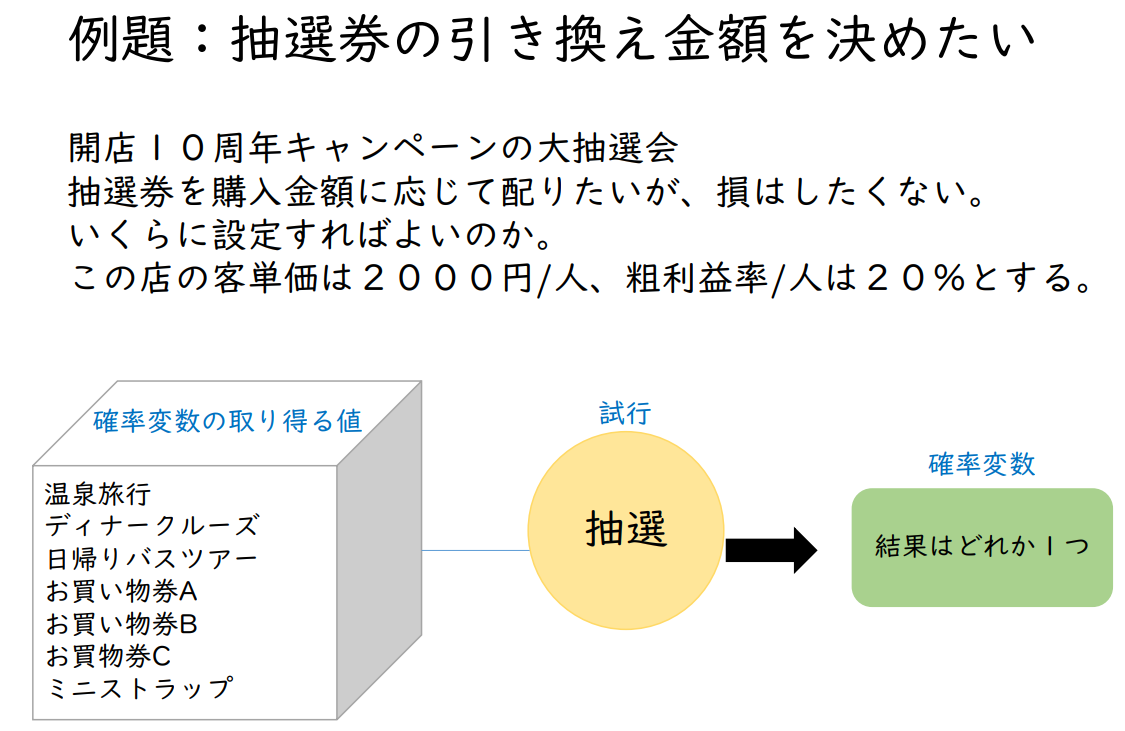
예시: 복권 교환 금액을 결정하고 싶다.
개점 10주년 캠페인의 대추첨회
구매 금액에 따라 추첨권을 나눠주고 싶지만, 손해는 보고 싶지 않다.
얼마로 설정하면 좋을까?
이 가게의 객단가는 2,000엔/명, 매출총이익률은 20%라고 가정한다.
| 확률 변수의 취할 수 있는 값 | 시행 | 확률 변수 |
| 온천 여행 디너 크루즈 당일치기 버스 투어 상품권 A 쇼핑권 B 쇼핑권 C 미니 스트랩 |
추첨 | 결과 중 하나 |
| 모집단에서 무작위로 표본을 계속 추출하면 표본 평균값의 평균값은 모평균에 수렴한다. |
| ↓ |
| 경품의 당첨금액은 책당 금액=시도 횟수당 평균값 |

개점 10주년 캠페인

답변
기대치 = 274엔
이 가게의 객단가는 2,000엔/명, 한계이익률/명은 20%로 한다.
한계이익 = 400엔
400엔 > 274엔
2,000엔 이상 영수증으로 1회 추첨

표본 평균의 분포는 정규분포를 따른다.
모평균 μ, 모분산 σ²에 대해 모집단에서 n 크기의 표본을 무작위로 추출한다.
표본 n이 크면 그 표본 평균의 분포는 정규분포를 따른다.
모집단이 어떤 분포이든 표본 평균은 정규분포에 근사하게 된다.
중심극한정리

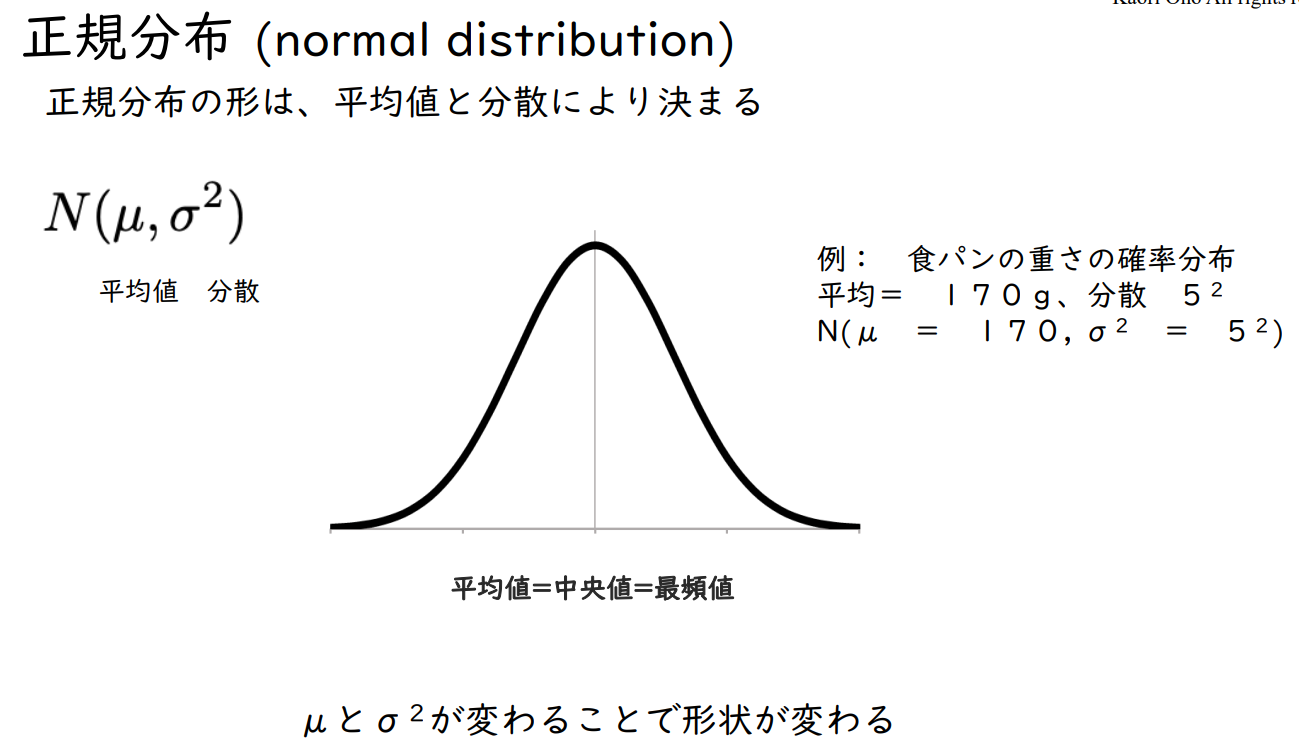
정규분포 (normal distribution)
정규분포의 형태는 평균과 분산에 의해 결정된다.
N ( μ , σ² )
예: 식빵 무게의 확률 분포
평균 = 170 g , 분산 5²
N ( μ = 170 , σ² = 5² )
μ와 σ²의 변화에 따라 모양이 달라집니다.
표준화
다양한 데이터의 단위 및 변동 범위를 일치시킵니다.
N ( μ , σ² ) → N ( 0 , 1 )
Z = ( X - μ ) / σ
평균을 빼고 표준편차로 나누기
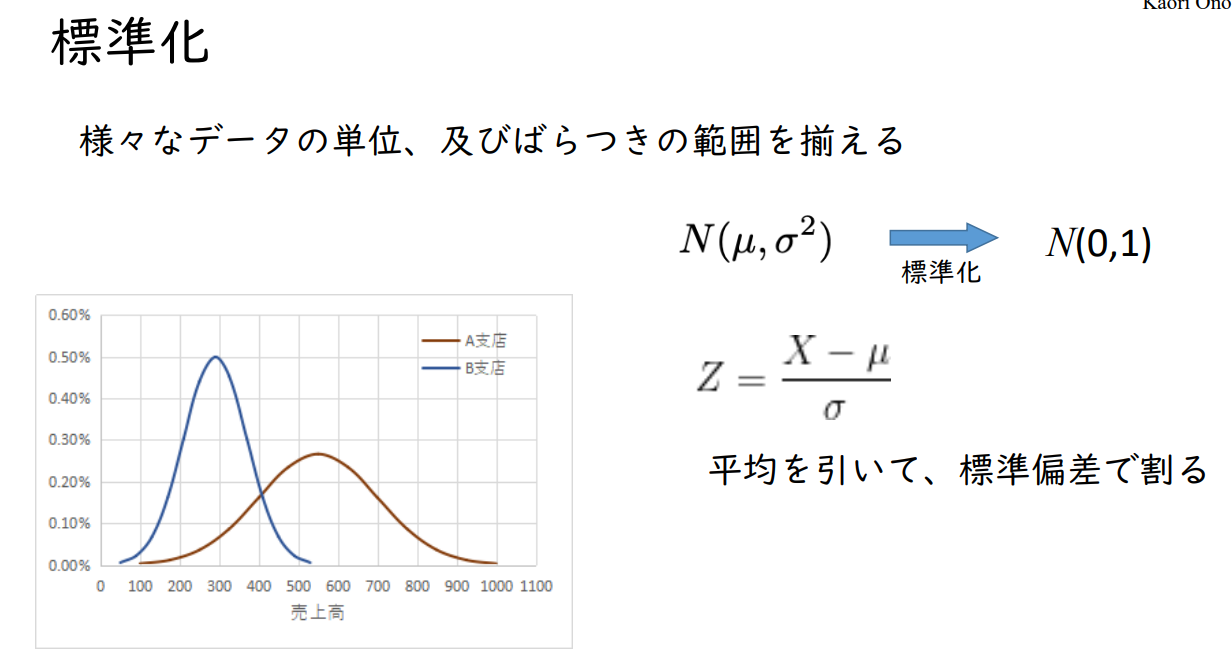
표준 정규분포 (Standard normal distribution)
정규분포의 평균값을 0, 표준편차를 1로 환산한 분포 = 정규분포의 표준화
| 확률 | ||
| 평균 ±1 표준편차 | 68.3% | |
| 평균 ±2 표준편차 | 95.4% | |
| 평균 ±3 표준편차 | 99.7% | |
| 신뢰도 계수 신뢰도 |
||
표준 정규 분포 데이터 세트 -∞ ~ +∞의 데이터 세트
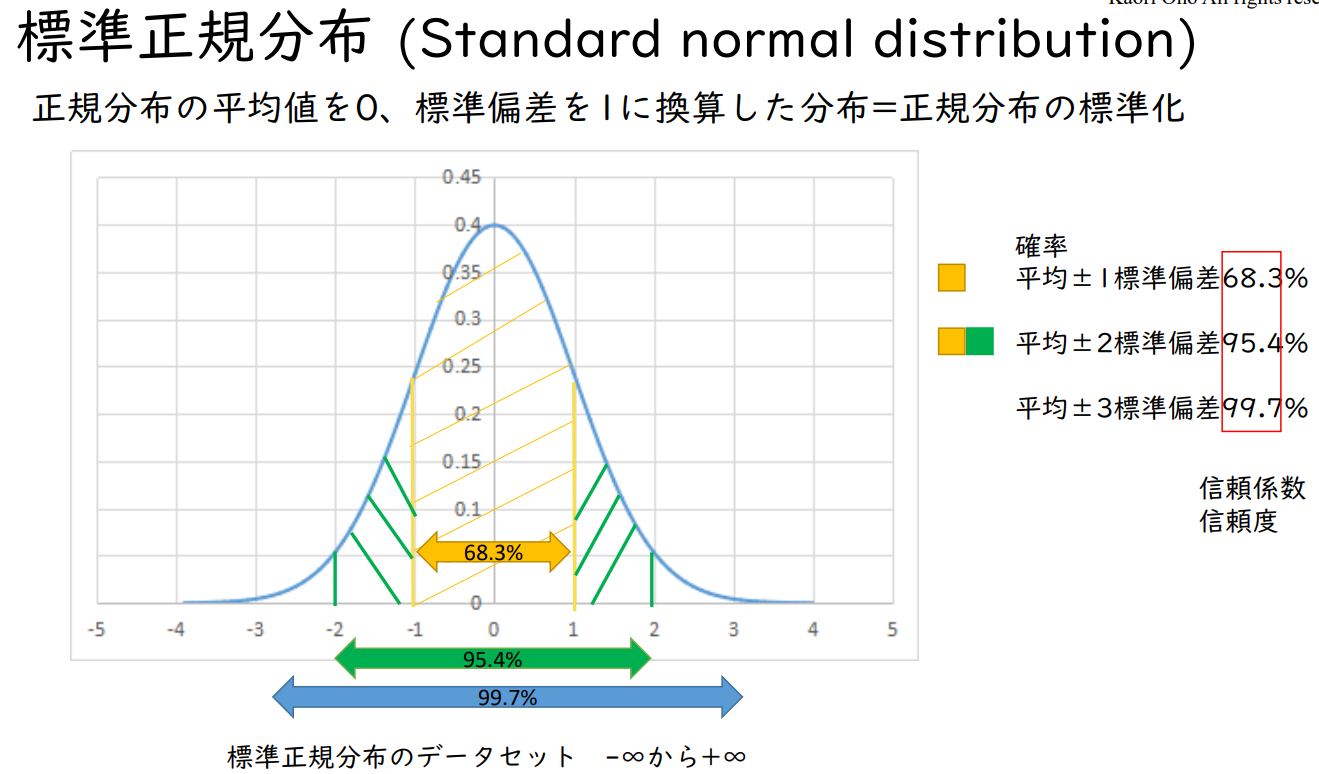
연습문제
한 공장에서 특수한 기구를 생산하고 있다.
기구의 폭의 평균값은 100mm입니다.
이 기구의 폭의 표준편차는 2mm인 것으로 알려져 있다.
이 기구의 폭이 98mm 이하가 될 확률은 몇 %입니까?

연습문제의 해답
평균값 0 이하 = 1 / 2 = 0.5
1 표준편차의 절반 = 0.683 / 2 = 0.3413
0.5 - 0.3413 = 0.1587 약 16%
96mm 이하인 경우
0.5 - 0.3413 - 0.1357 = 0.023 2.3%.
표준 정규분포표에서 계산
예시
기구 폭의 평균값은 100mm
기구 폭의 표준편차는 2mm
공장에서 생산된 기구를 무작위로 추출하여 그 기구의 폭이 97mm 이상 105mm 이하일 확률을 알고 싶다.
표준화
( 97 - 100 ) / 2 = -1.5
( 105 - 100 ) / 2 = 2.5
P ( 97 ≦ X ≦ 105 ) = P ( -1.5 ≦ Z ≦ 2.5 )
= P ( 0 ≦ Z ≦ 1.5 ) + P ( 0 ≦ Z ≦ 2.5 )
= 0.4332 + 0.4938
= 0.927
92.7%

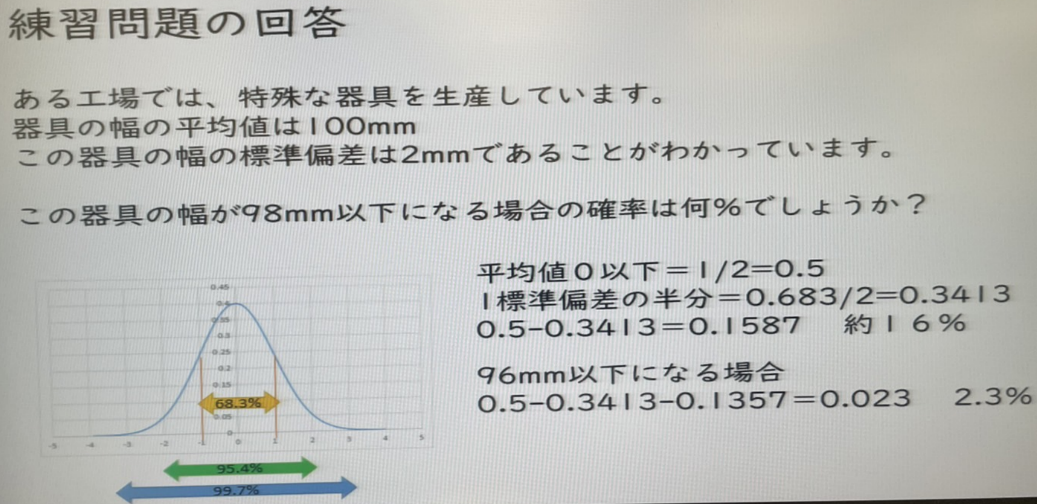
표준 정규분포표 보는 법
특정 Z값 이상이 발생할 확률
녹색 부분이 생길 확률
p ( 0 ≦ z ≦ 1.5 ) + p ( 0 ≦ z ≦ 2.5 )
0.5 - 0.066807 = 0.433193
0.5 - 0.00621 = 0.49379
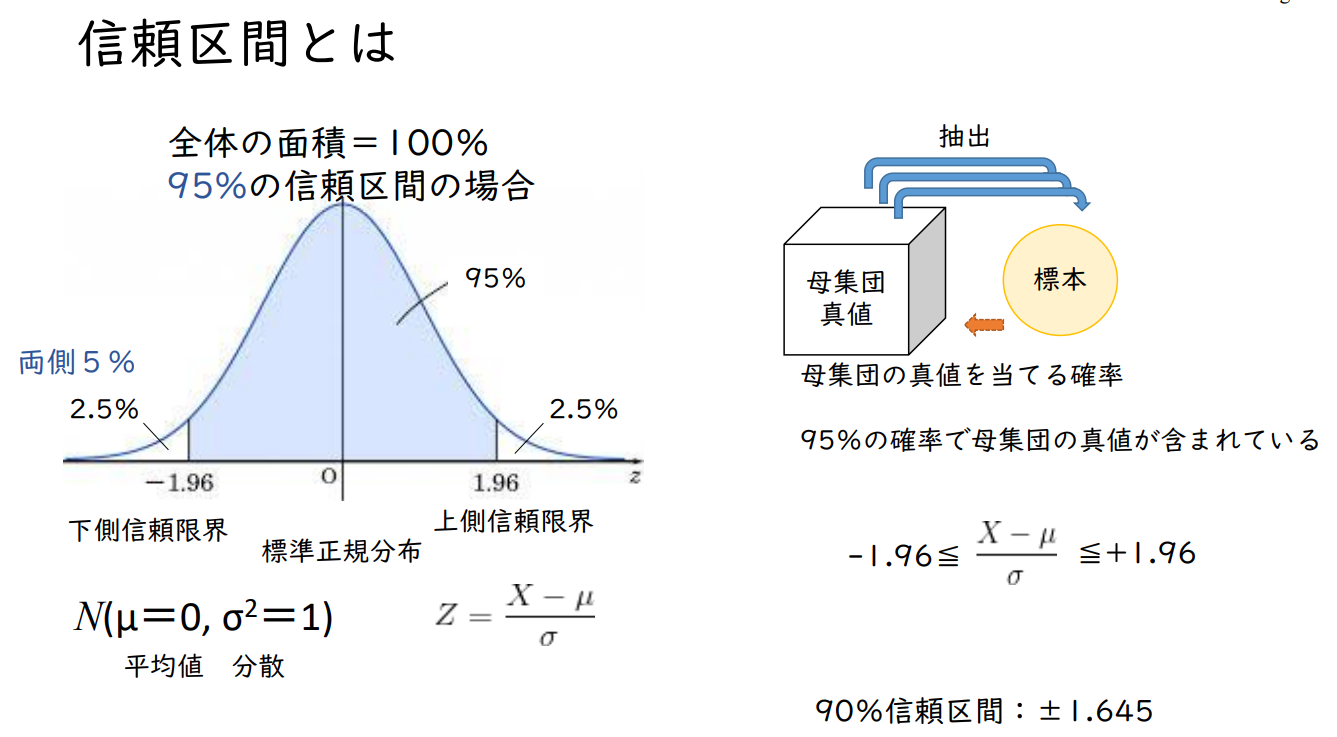
신뢰구간이란?
전체 면적 = 100
95% 신뢰구간의 경우
모집단의 참값을 맞힐 확률
95%의 확률로 모집단의 참값을 포함한다.
-1.96 ≦ ( X - μ ) / σ ≦ +1.96
90% 신뢰 구간 : ±1.645
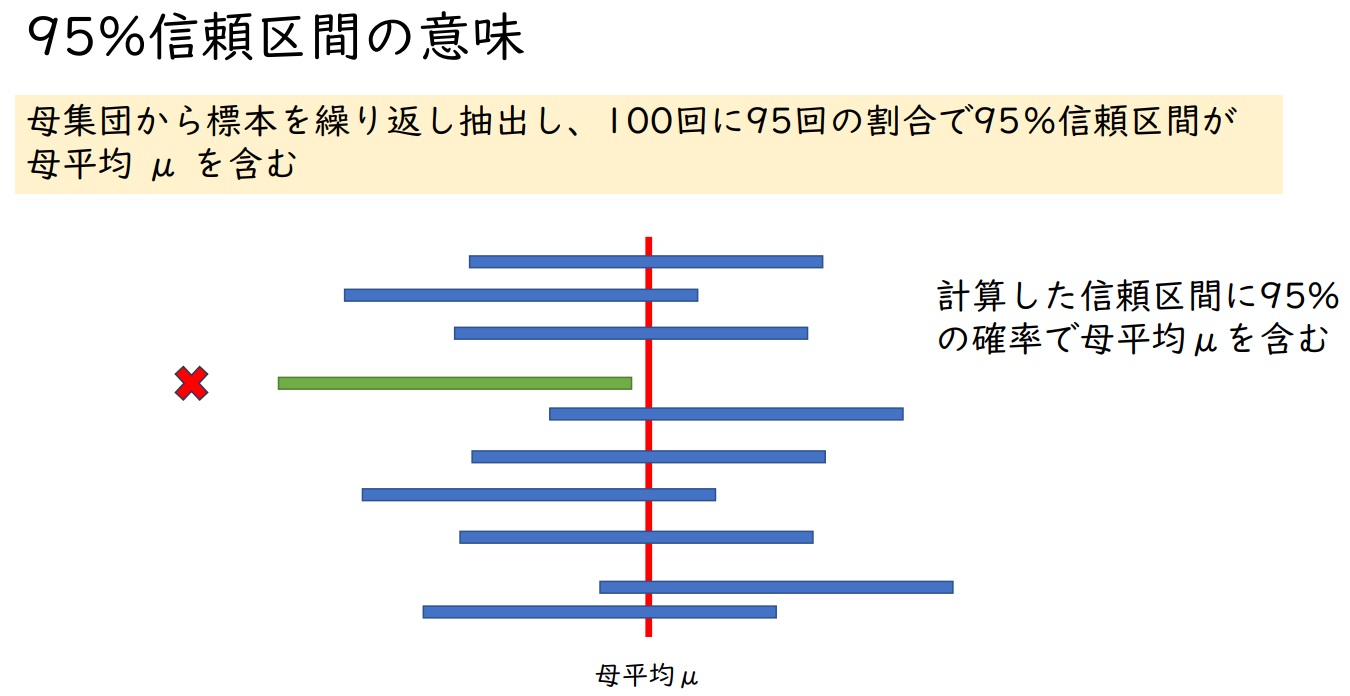
95% 신뢰구간의 의미
모집단에서 표본을 반복적으로 추출하여 100번 중 95번의 비율로 95% 신뢰구간이 모평균 μ를 포함한다.
계산된 신뢰 구간에 95% 확률로 모평균 μ 포함
표준오차(Standard Error; SE)
SD = 확률변수 Xᵢ 의 표준편차(표본표준편차)
SE = n개 확률변수 X₁ ∼ Xₙ 의 표본 평균의 표준편차
SE = SD / √n
데이터 수가 많을수록 SE는 작아진다.
⇒ 표본에서 얻어진 추정량의 오차(편차)
편차 = 데이터의 값 - 평균값
분산 = 편차의 제곱의 합 ÷ 변수 데이터의 값
표준편차(SD) = 분산의 제곱근


예시
한 산업군 36개 기업의 ROA의 표본 표준편차가 12%라고 가정하자.
평균값의 표준오차는 다음과 같습니다.
SE = 12 / √36 = 2%

모평균의 신뢰구간
모평균은 표본평균 ±〇〇의 범위 + '이 신뢰 구간에 들어가는 신뢰도는 95%'입니다.
95% 신뢰구간 = X ± 1.96 x SE
SE = SD / √n
중심극한정리는 모집단이 어떤 분포를 가지고 있든,
거기서 무작위로 추출한 n개의 표본 크기가 크다면 표본 평균의 분포는 정규분포를 따른다는 것이다.

예시
한 공장에서 무게가 100g이 되도록 아이스크림을 생산하고 있습니다.
이제 공장의 기계가 정해진 대로 작동하는지 확인하고 싶습니다.
아이스크림을 무작위로 49개를 꺼내어 측정한 결과, 표본 평균은 106g, 표본 분산이 196이었습니다.

표준오차 SE = √196 / √49 = 14 / 7 = 2
모평균의 95% 신뢰구간
표본평균 106 ± 95% 신뢰구간 1.96 x 2
102.08부터 109.92의 범위

Q답변
1. A씨가 시험을 치렀는데, 그 결과 편차값이 70이었습니다.
이 시험은 10만 명의 학생이 응시했습니다.
이 때, A 씨보다 성적이 좋은 사람은 총 몇 명이나 있었을까요?
편차값
평균=50, 표준편차=10
편차=70, 2배 표준편차
평균값 + 1.96 x 표준편차 2 -> 2.5%
10만명 중 2.5%는 2,500명


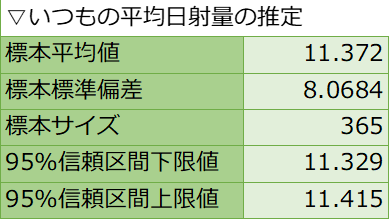
예시: 엑셀을 이용한 계산
95%의 신뢰도로 평균 일사량을 맞추고 싶다.


설명 검정(통계적 가설 검정)

가설검정이란
1) 모집단에 대해 가설을 설정하고,
2) 표본을 이용하여 그 가설이 옳은지 여부를 검증하여
3) 가설에 대한 결론을 도출하는 것
- 구간추정과 같은 개념
- 확률론을 이용하여 통계적 방법으로 검증하는 것
- 분산이 필요 (분산을 모르면 분포의 그림을 알 수 없음 - > 기각범위를 설정할 수 없음)

부정하고 싶은 가설을 기각함으로써 주장하고 싶은 가설을 지지한다.
가설
귀무가설(null hypothesis) : 부정하고자 하는 가설
예: 모집단의 평균 수익률은 -0.5%이다.
대립가설(alternative hypothesis) : 주장하고자 하는 가설
예: 모집단의 평균 수익률은 -0.5%가 아니다.
'모평균은 μ₀ 이다'라는 가설을 설정한다.
귀무가설 H0 : μₓ = μ₀
대립가설 H1 : μₓ ≠ μ₀

- 검정 시 사용하는 통계량 = 확률변수
- 귀무가설이 옳다고 가정했을 때,
그 검정통계량(관찰된 사건보다 더 드문 일이 일어날 확률을 계산하기 위한 값)의 확률 분포를 계산
사례 1 : 확률적으로 드물게만 일어날 수 있는 경우
이렇게 희귀한 일은 일어나지 않아야 하므로 귀무가설이 옳다는 가정이 틀린 것이 아닌가.
따라서 이 귀무가설은 기각. 대립가설을 채택.
사례 2 : 확률적으로 나름대로 일어난다.
나름대로 일어나는 일이므로 귀무가설을 기각할 수 있을 만큼 충분한 통계적 증거가 없다.
따라서 귀무가설을 기각할 수 없다/귀무가설을 채택한다.
"귀무가설을 기각할 수 있을 만큼 충분한 통계적 증거가 없다"

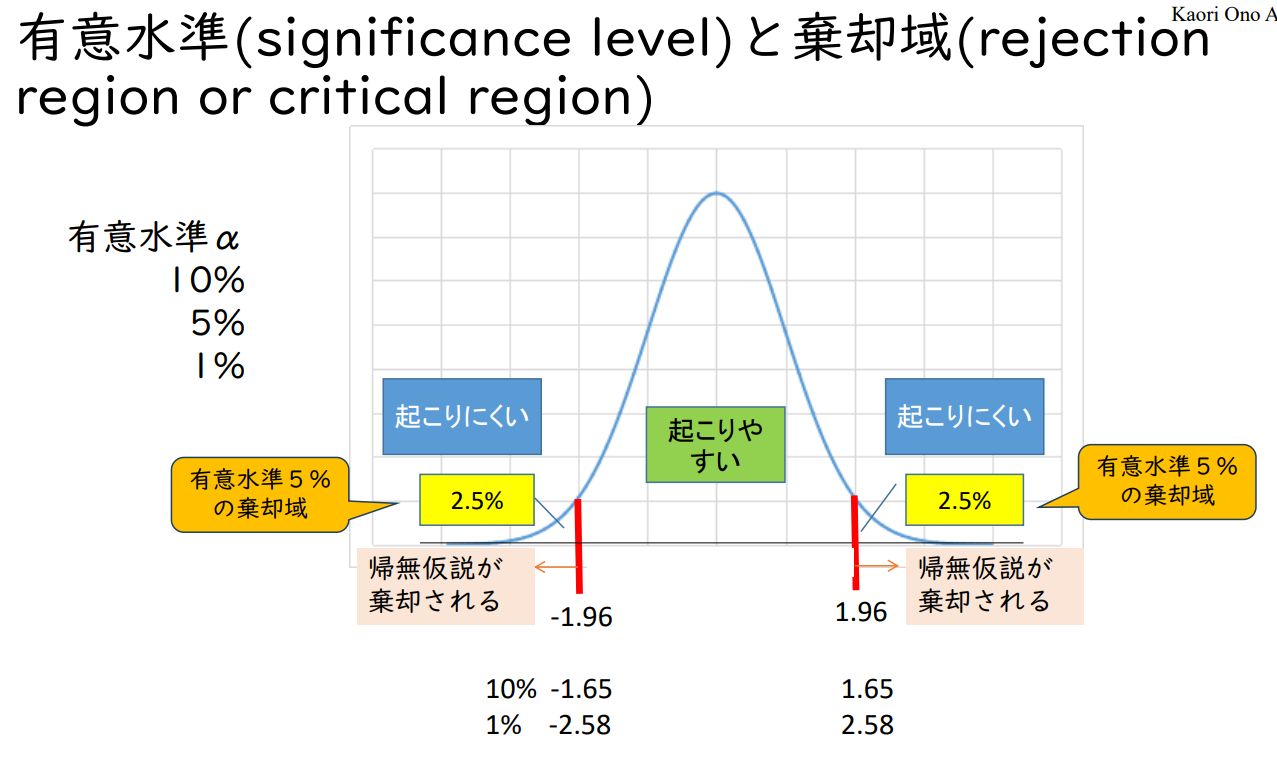
유의수준(significance level)과 기각영역(rejection region or critical region)
유의수준 α ( 10%, 5%, 1% )
| 일어나기 어려움 | 일어나기 쉬움 | 일어나기 어려움 |
| 2.5% 유의수준 5%의 기각영역 |
2.5% 유의수준 5%의 기각영역 |
|
| -1.96 귀무가설이 기각됨 |
+1.96 귀무가설이 기각됨 |
|
| 10% -1.65 1% -2.58 |
+1.65 +2.58 |
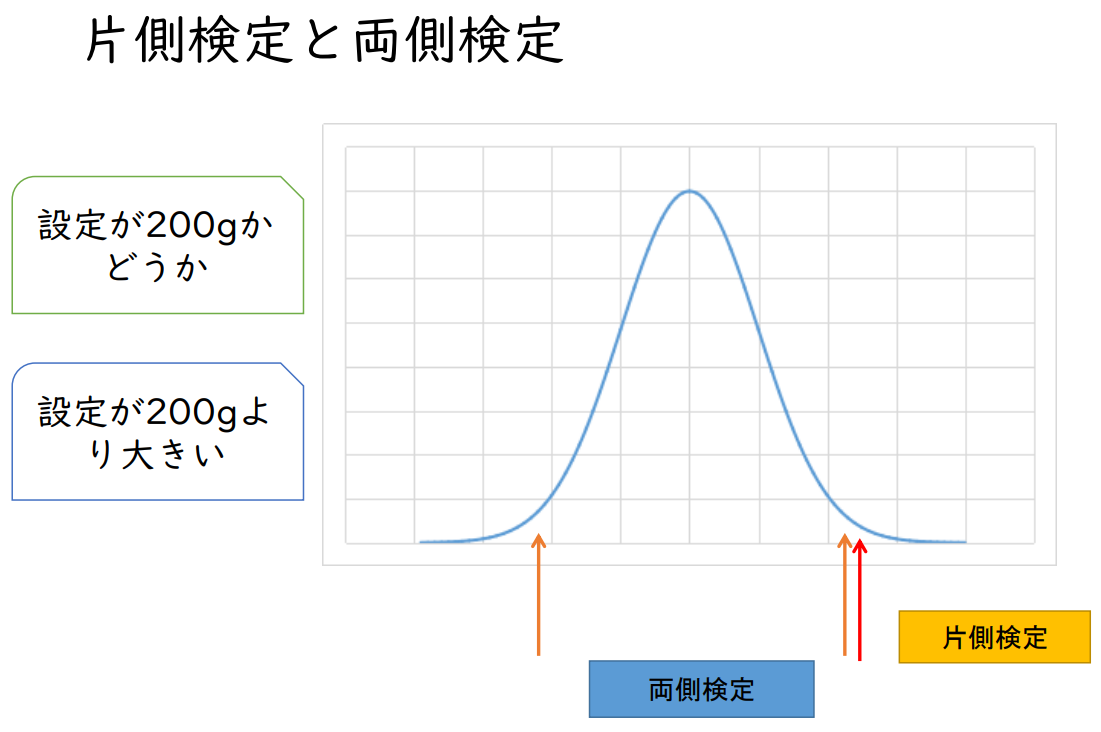
일측 검사와 양측 검사
설정이 200g인지 아닌지
설정이 200g보다 크다
1표본 t검정(one sample t-test)
사용하는 목적
모집단의 값이 자신이 가정한 값과 동일한지 여부 확인
전제조건
- 모집단의 분산을 알 수 없는 경우
- 적은 표본만 모을 수 있는 경우
모집단 분산을 모르기 때문에 표본 데이터를 사용하여 불균등 분산에 의한 표준편차로 대용
* 표본분산(추정량)은 표본 데이터 수(N)가 커질수록 높은 확률로 모분산(σ²)에 가까워진다.

편차(SD) = 표본값 - 평균값
분산(불균형 분산) = { (편차의 제곱)의 합계 } / ( 표본 수 - 1 )
표본 평균의 평균값의 표준편차 = 표준오차(SE)
표준오차(SE) = ( 분산 / 표본수 ) 제곱근 = 표본 표준편차(SD) / 표본수(n)의 제곱근
예시
어떤 공장에서는 무게가 200g(확률변수)이 되도록 설정하여 햄버거를 생산하고 있다.
무작위로 10개의 샘플을 추출하여 측정한 결과, 표본 평균은 203g이었습니다.
설정이 200g으로 가정하고 있었기 때문에 이 차이가 우연인지,
아니면 기계 설정에 문제가 있다고 보는 것이 좋을지 궁금합니다.
[205, 198 ,197 , 208 , 204 , 202 , 207 , 199 , 207 , 203 ] g
분산 : ( 205 - 200 )² + ( 198 - 200 )² ... = 140
분산 : 140 / ( 10 - 1 ) = 15.6
표준오차 = 표준편차 3.9(=√15.6) / 3.16(√10개) = 1.23

1표본의 t검정
- 가설을 세운다.
귀무가설 H0 : μ = 200
대립가설 H1 : μ ≠ 200 - t값을 계산한다.
=( 표본평균 203 - 확률변수 200 ) / 표준오차 1.23 = 2.4
t = ( x - μ₀ ) / SE - t값의 절대값이 1.96보다 크다 -> 유의수준 5%에서 귀무가설 H0 기각(거의 일어나지 않는 현상)
기계의 설정이 200g이라는 것에 문제가 있다고 생각된다.

2. 구조조정은 기업의 주가에 어떤 영향을 미치는가?
조기 희망퇴직을 모집한다고 발표한 100개 기업의 공시일 기준 주가 변동에 대한 데이터를 입수했다.
수익률의 평균은 -1.4%, 표준오차는 0.7%였다.
'조기 희망퇴직을 모집한 기업의 주가는 하락한다'는 것이 통계적으로 유의미하다고 할 수 있을까?


귀무가설 H0 : 수익률 = 0
대립가설 H1 : 수익률 ≠ 0
t값 = ( 표본평균 -1.4 - 0 ) / 표준오차 0.7 = - 2
평균값이 마이너스이므로 t값이 -1.96보다 작으면 유의수준 5%에서 유의.
수익률 = 0이라는 귀무가설을 기각할 수 있으므로 주가는 하락하고 있다고 할 수 있다.

2표본 t검정(two sample t-test)
두 그룹의 평균값에 차이가 있는지 검정
예시
남성 직원과 여성 직원의 초봉 평균값의 차이
금연자와 비흡연자의 콜레스테롤 평균값의 차이
남성 직원과 여성 직원의 과장 승급 시 평균 연령 차이
- 대응하는 2표본 t검정 : 첫 번째 표본과 두 번째 표본이 대응한다. = 표본은 동일
예: 피험자에게 어떤 약을 투여하기 전과 후의 혈압이 어떻게 변화했는지 - 대응하지 않는 2표본 t검정 : 비교하는 데이터 외의 다른 요소도 다르다.
예: A 지점의 매출액과 B 지점의 매출액

t값 = 검정통계량 (test statistics)
첫 번째 그룹의 표본 평균 = X
두 번째 그룹의 표본 평균 = Y
- 가설 세우기
귀무가설 H0 : μₓ = μʸ
대립가설 H1 : μₓ ≠ μʸ - 표본 평균의 차이의 표준오차를 계산한다.
SE= √ { ( X의 표본 분산 / X의 표본 수 ) + ( Y의 표본 분산 / Y의 표본 수 ) } - t값 계산
t = ( X의 표본 평균 - Y의 표본 평균 ) / SE
t값의 절대값이 1.96보다 큰 경우 → '모평균의 차이는 0이다'라는 귀무가설 H0은 유의수준 5%에서 기각
t값 = 검정통계량 (test statistics)

p값(P-value) : 유의확률
p값은 (0.000~1) 사이에서 산출되는 값으로, 귀무가설을 기각할지 여부를 판단하는 기준으로 사용되는 수치입니다.
일본인의 젊은 층과 노년층에 따라 월간 독서량에 차이가 있는지 검증하기 위해 설문조사를 실시하여
300명 분량의 데이터를 수집할 수 있었다고 가정해 봅시다.
그 데이터를 이용하여 젊은 층과 노년층의 그룹 간 비교를 하고 싶기 때문에
이번에는 대응표본 t검정을 실시했다고 가정해 봅시다.
각 군 간의 평균과 표준편차는 청년층( X = 2.37, SD = 1.41 ), 노년층( X = 4.71, SD = 0.57 )이라고 가정해봅시다.
그리고 t검정 결과 ( t값 = 2.17, p < 0.05 )의 결과가 나왔다고 하자.
( p < 0.05 )가 p값 이며, 유의수준을 의미합니다.
유의수준은 산출된 p값을 이용하여 그 분석 결과가 유의미한지 판단하는 기준이며,
일반적으로 p값이 (0.05) 이하인 것을 유의미하다고 판단한다.

p값의 정의
p값은 구한 분석 결과가 귀무가설일 확률을 나타내는 수치로
귀무가설이 맞음에도 불구하고, 잘못하여 대립가설을 채택할 확률
p값이 5% 미만( p < 0.05)인 경우 귀무가설이 발생할 수 있는 확률은 5%(대립가설 발생 확률은 95%)이며,
해당 연구에서 대립가설이 발생한 것은 우연이 아니라고 판단하여
귀무가설을 기각하고 대립가설을 채택하는 것이 일반적이다.
p값이 5%를 초과하더라도 10% 미만인 경우 ( p < 0.1 )는 유의미한 경향이 있다고 표기하기도 한다.
유의수준의 정의
유의수준이란 통계적 가설검정을 실시하여 얻어진 p값을 이용하여 귀무가설을 기각할지 여부를 판단하는 기준
일반적으로 p값이 5% 미만이면 귀무가설을 기각할 수 있다고 판단.
표1. 유의수준 조견표
| 유의수준 | 설명기호 | ||
| 강 | p < 0.001 | *** | |
| 중 | 유의 | p < 0.01 | ** |
| 약 | p < 0.05 | * | |
| 유의경향 | p < 0.1 | ||
| 비유의 | p ≧ 0.1 | n. s. |

데이터 해석의 표현 방식에 주의
p값(유의확률)
유의미한 차이 있음 (p < 0.05)
100%는 아니지만 차이가 있다는 증거 중 하나
유의미한 차이 없음
귀무가설이 맞는지 대립가설이 맞는지 알 수 없음(차이가 있는지 없는지 알 수 없음).
"통계적으로 유의미한 차이를 발견할 수 없었다."
× "같았다."
× "귀무가설 H0이 옳았다."

'WBS - 2023 Winter > 기업 데이터 분석' 카테고리의 다른 글
| (기업데이터 #13-14) 패널데이터, 회귀분석 정리 (0) | 2024.01.27 |
|---|---|
| (기업데이터 #11-12) 더미 변수, 교차항, 로지스틱 회귀 분석 (0) | 2024.01.20 |
| (기업데이터 #9-10) 다중회귀분석 (0) | 2024.01.13 |
| (데이터 #7-8) 연구 방법, 논문 작성 (0) | 2023.12.23 |
| (데이터 #5-6) 데이터 간의 관계 파악 | 상관관계, 인과관계, 단회귀 분석 (0) | 2023.12.16 |
| (데이터 #1-2) Introduction (0) | 2023.12.04 |



