9, 10회 다중회귀분석

지난번의 후속편

- 기술통계 : 얻은 데이터에서 그 특징을 추출(정리)한다.
- 추측통계 : 부분으로부터 전체를 추측하는 것
- 통계적 추정 : 표본 데이터로부터 모집단 추정
방법 : 점추정, 구간추정 - 통계적 가설검정 : 모집단에 대한 가설이 성립하는지 여부를 검정하는 것
방법 : t검정, F검정... - 회귀분석 : Y(종속변수)가 H(독립변수)에 얼마나 영향을 미치는지 관계를 설명
(혹은 예측에 사용하고자 하는 경우)
방법 : 선형회귀모형, 이항로짓모형...
- 통계적 추정 : 표본 데이터로부터 모집단 추정

통계적 추정
모집단의 평균이나 표준편차를 알 수 없을 때 표본의 통계량으로 모집단 수(모집단의 값)를 추정하는 방법
- 점 추정
- 표본 → 모평균
- 표본분산 → 불균형분산 → 모분산
- 구간 추정
- 신뢰 구간에 따라 "모평균은 표본 평균값 ±〇〇의 범위에 있다고 추정한다."

중심극한정리는 모집단이 어떤 분포를 가지고 있든, 거기서 무작위로 추출한 n개의 표본 크기가 크다면
표본 평균의 분포는 정규분포를 따른다는 것이다.
표준정규분포: 정규분포의 평균값을 0, 표준편차를 1로 환산한 분포 = 정규분포의 표준화
95% 적중
-1.96 이상 +1.96 이하
99% 적중
-2.58 이상 +2.58 이하

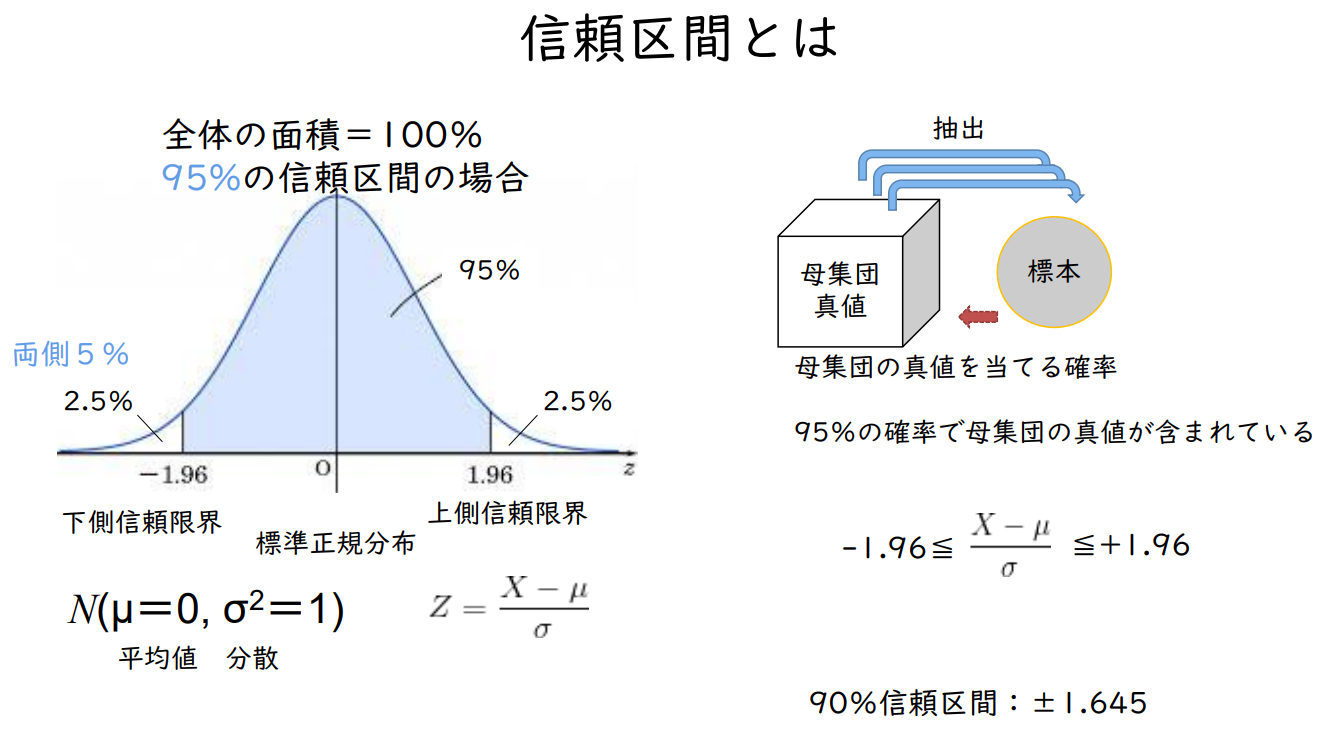
신뢰구간이란?
전체 면적 = 100
95% 신뢰구간의 경우
모집단의 참값을 맞출 확률
95%의 확률로 모집단의 참값을 포함한다.
90% 신뢰 구간: ±1.645
모평균 구간 추정 예시
✓ 공장에서 아이스크림을 제조하는 기계의 정확도 확인
✓ 아키타현의 평균 일사량 추정
✓ 일본 성인 남성의 콜레스테롤 평균값 추정
"모평균을 표본 평균값 ±〇〇〇의 범위에 맞추는 것."

복습 문제
편의점에 주먹밥을 자동으로 제조하는 기계가 있다.
이 기계는 주먹밥의 무게를 다양하게 조절할 수 있지만, 물론 기계이기 때문에 무게에 오차가 발생한다.
무작위로 추출한 100개의 주먹밥 무게의 평균은 80g, 표준편차는 10g이었다.
이때 제조된 주먹밥의 평균 무게(모평균)를 μ라고 할 때, μ의 신뢰도 90%의 신뢰구간을 구하시오.
참고: 코지마 히로유키 (2013) 통계학입문 다이아몬드사
95% 신뢰구간의 경우 = X ±1.96 X SE

답변
문제 문장에서 표본 평균과 표준편차는 다음과 같습니다.
X = 80, 표준편차 = 10
표본의 크기가 충분히 크므로 중심극한정리에서 표본 평균은 정규분포에 따라 90% 신뢰구간 = 1.64
X + 1.64 X SE
80 - 1.64 x 10 / √100 ≤ μ ≤ 80 + 1.64 x 10 / √100
80 - 1.64 x 1 ≤ μ ≤ 80 + 1.64 x 1
78.36 ≤ μ ≤ 81.64


추정의 적용 사례
어떤 선거에 후보 A와 후보 B가 출마했다.
후보 A의 득표율을 p라고 하자.
투표를 마친 유권자 400명(n)을 무작위로 추출하여 투표한 후보를 물었더니,
그 중 300명이 A 후보에게 투표했고, 176명이 B 후보에게 투표했다고 답했다.
A의 득표율은 p = 224 / 400 = 0.56 ← 이 값은 일점 추정치이므로 점추정
0.56이라는 득표율이 얼마나 신뢰성이 있는 것일까?
득표율 56% 신뢰도 95% 신뢰구간 = 0.51 ~ 0.61 p ± 1.96 √ ( p ( 1 - p ) / n )
후보자가 2명인 경우의 '당락'은 구간의 하한이 50%를 넘으면 되기 때문에, "A 후보에게 당선이 나왔습니다!"

통계적 가설검정
모집단에 대한 가설('있어야 한다')에 대해 표본의 데이터로부터 계산한 검정량이 '있어야 한다'는 범위에 들어맞는지(채택범위), 들어맞지 않는지(기각범위)를 확률분포를 이용하여 조사하는 절차
귀무가설(null hypothesis) : 부정하고 싶은 가설
대립가설(alternative hypothesis) : 주장하고 싶은 가설
'모평균은 μ₀ 이다'라는 가설을 설정한다.
귀무가설 H₀ : μₓ = μ₀
대립가설 H₁ : μₓ ≠ μ₀

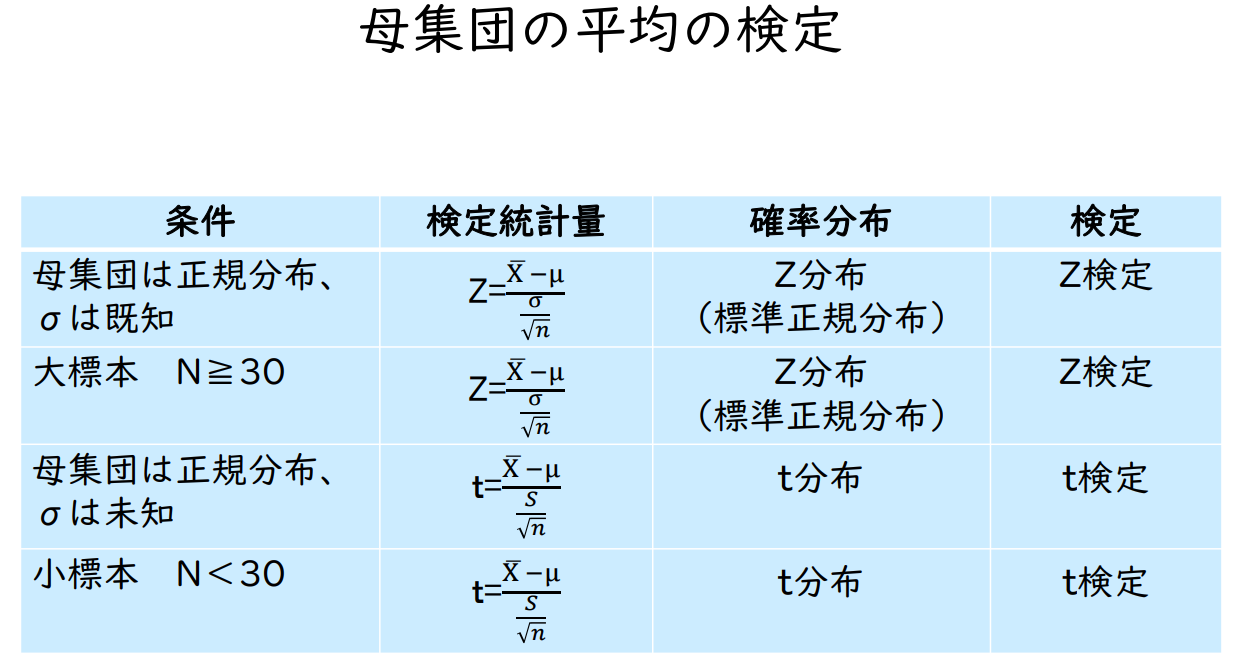
모집단 평균 검정
| 조건 | 검정통계량 | 확률분포 | 검정 |
| 모집단은 정규분포, σ는 알려져 있다. |
Z = ( X - μ ) / ( σ / √n ) | Z 분포 (표준정규분포) |
Z 검정 |
| 대표본 N ≧ 30 | Z = ( X - μ ) / ( σ / √n ) | Z 분포 (평균정규분포) |
Z 검정 |
| 모집단은 정규분포, σ는 알 수 없음 |
t = ( X - μ ) / ( S / √n ) | t 분포 | t 검정 |
| 소표본 N < 30 | t = ( X - μ ) / ( S / √n ) | t 분포 | t 검정 |
평균 검정의 예: 과거 데이터(모집단)와의 비교
과거 데이터에서 모집단 μ를 알 수 있다.
- 표본 데이터에서 올해 중학생의 기록이 예년보다 느린지 여부를 유의수준 5%로 검증하고 싶다.
- 4인 가족 1주일 식비의 작년 평균 μ = 88,102엔 과 올해 비교

가설의 세우는 방법과 기각 영역 (1)
4인 가족 1주일 식비의 작년 평균 μ = 88,102엔 과 올해 비교
계속 인플레이션이 지속되는 시대라면 대립가설을 어떻게 설정하고, α = 5% 의 기각영역은 어디에 위치해야 할까?
H₀ : μ = 88,102엔
H₁ : μ > 88,102엔
귀무가설은 식비가 작년에 비해 상승하지 않는다(동일)고 가정하고 대립가설은 상승한다고 가정한다.
따라서 기각 영역은 오른쪽이 된다.


가설 세우는 방법과 기각 영역 (2)
한 산업에 속한 100개 기업의 매출 성장률 평균은 2.4%였다.
그리고 표준편차는 8%였습니다.
이 때, 이 산업 전체에서 매출액이 증가하고 있다고 볼 수 있을까요?
| 가설 귀무가설 H₀ : 성장률 μ = 0 성장하지 않는다. 대립가설 H₁ : 성장률 μ > 0 성장하고 있는지 여부를 검정. 기각 영역은 오른쪽이 된다. |
Z값 = 3 3 > 1.96 유의수준 %에서 기각 3 > 2.58 유의수준 1%에서 기각 |

평균 검정의 예: 공장 품질 검사
길이 5mm 규격의 나사를 만들고 있을 때, 생산한 나사가 제대로 5mm가 되는지 여부를 통계적 가설검정을 할 때
- 귀무가설 μ=5
- 대립가설 μ ≠ 5
라는 가설을 세우고, 표본의 평균값인 μ = 5 와 얼마나 차이가 나는지 검정합니다.

상관계수는 반드시 -1과 1 사이의 값을 취한다.
| -1 | 0 | 1 |
| 완전한 부의 상관 | 상관관계 없음 | 완전한 정의 상관 |
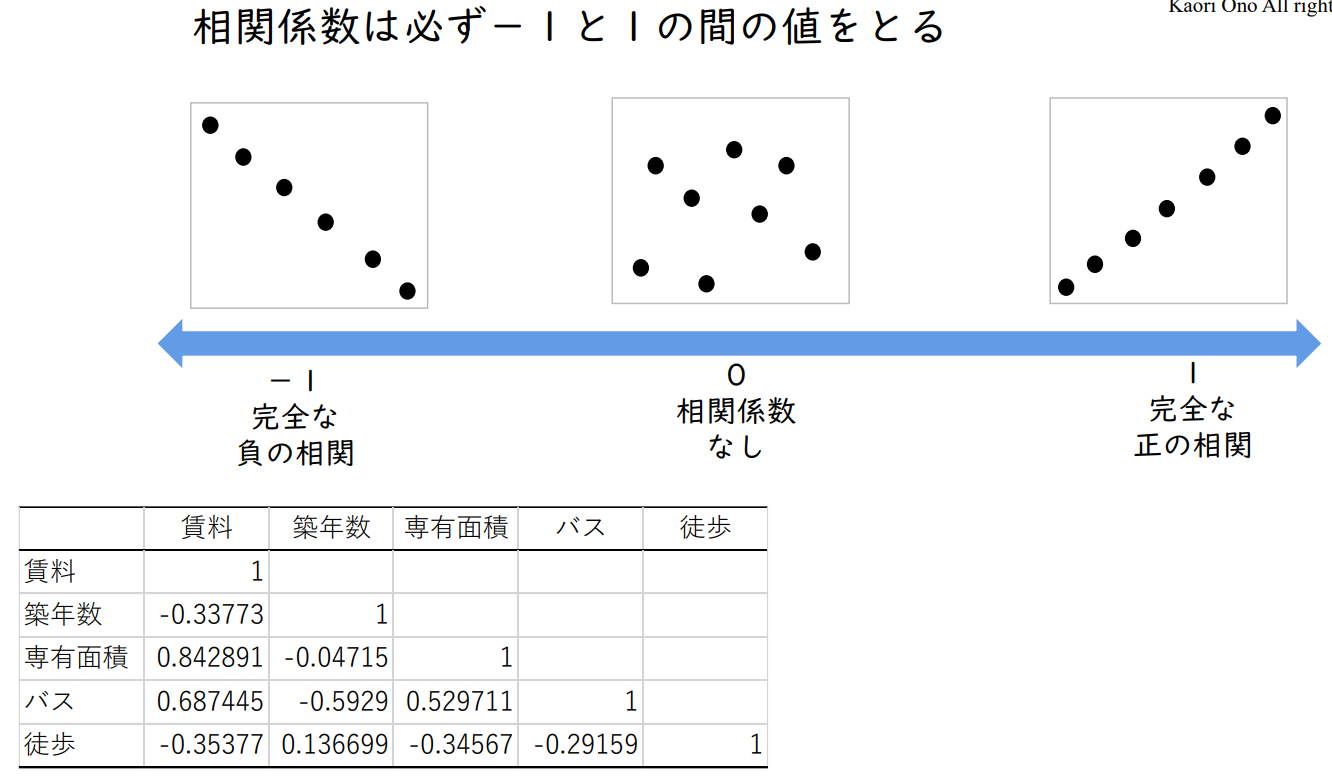
- 임대료와 건축연수 간에는 음의 상관관계(-0.34)
- 임대료와 전용면적 사이에는 강한 양의 상관관계 있음(0.84)
- 건축년수와 전용면적 사이에는 상관관계가 없거나 있어도 약한 음의 상관관계(-0.05)

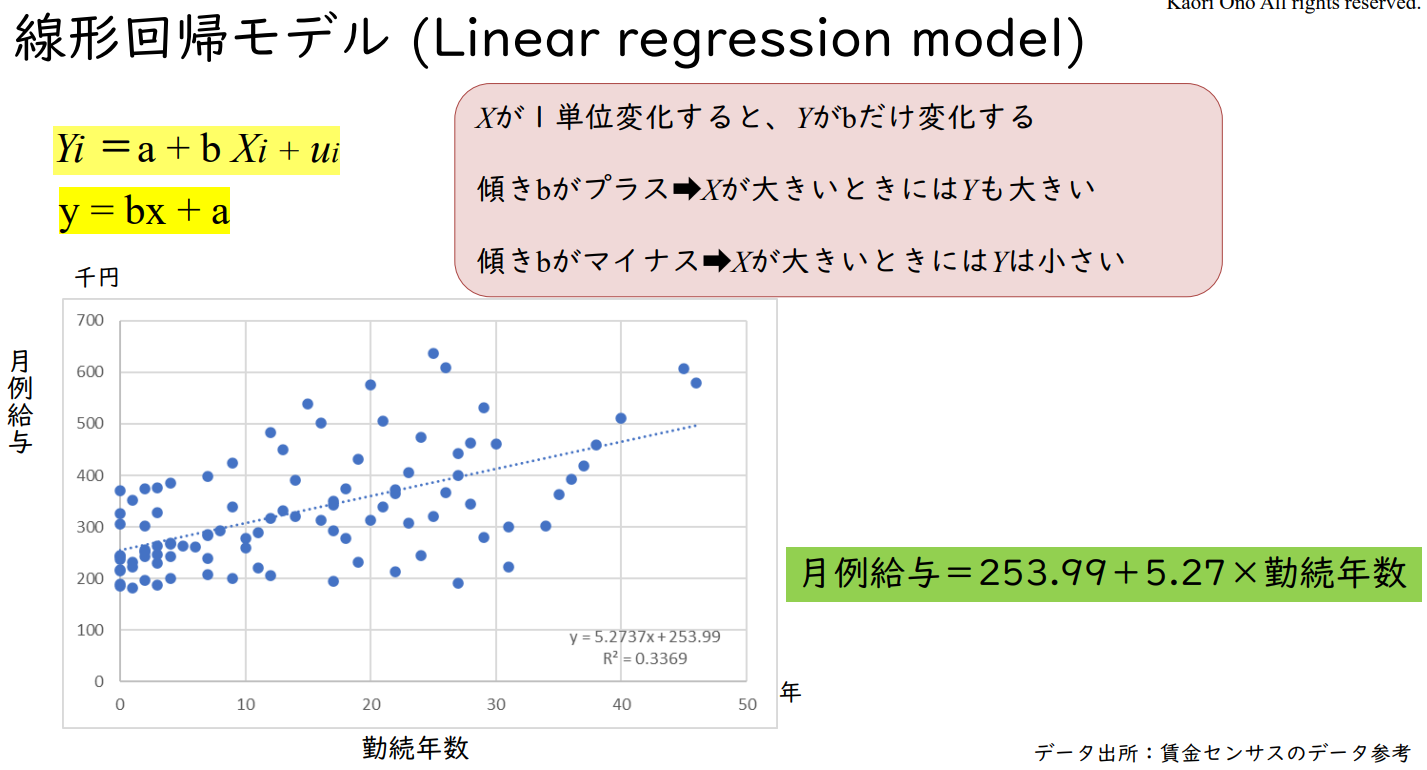
선형회귀모형 (Linear regression model)
Yᵢ = a + b Xᵢ + uᵢ
y = bx + a
X가 1단위 변화하면 Y가 b만큼 변화한다.
기울기 b가 플러스 → X가 클 때는 Y도 크다.
기울기 b가 마이너스 → X가 클 때 Y는 작다.
월급 = 253.99 + 5.27 × 근속연수
설명변수의 타당성 확인
- 모델이 얼마나 잘 설명할 수 있었는지: 결정계수 ( R² )
- 변수 X가 변수 Y에 영향을 미치는지 여부(얻어진 계수에 의미가 있는지 여부) : t 검정

결정계수 ( Coefficient of Determination / R-squared / R² )
설명변수 x가 피설명변수 y를 모델에 의해 설명할 수 있는 비율.
- 결정계수는 0 과 1 사이의 수치를 취한다.
- 모델이 피설명변수의 움직임을 완전히 설명하면 1, 전혀 설명하지 못하면 0이다.
- 설명변수를 늘릴수록 1에 가까워진다.

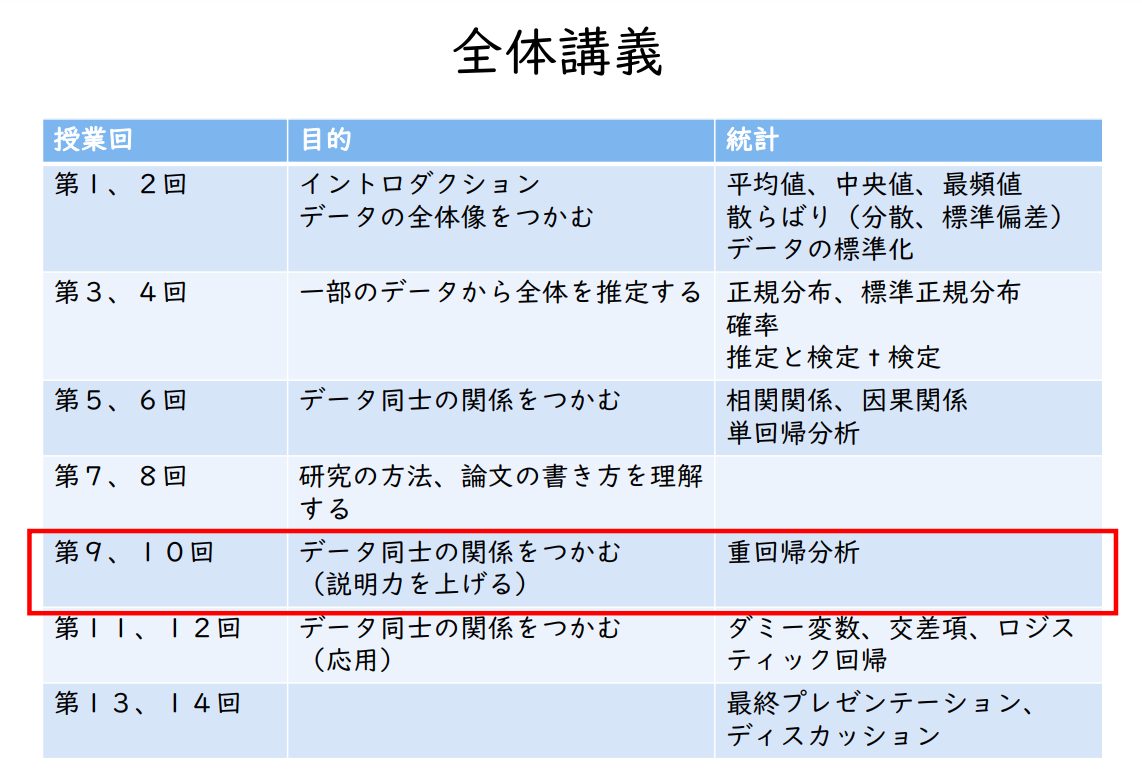
검정 결과 판단
기각의 판단은 일반적으로 p값을 사용
p값 : 귀무가설이 성립할 경우, 그 데이터가 얼마나 가능성이 없는 데이터인지를 나타내는 확률.
유의수준 5%의 예
p값 < 유의수준 0.05 귀무가설을 기각하고 대립가설을 채택, 유의미한 차이가 있다고 할 수 있다.
p값 ≧ 유효수준 0.05 대립가설을 채택하지 못하여 유의미한 차이가 있다고 할 수 없다.
유의수준 10% : p값이 10% 이하인 경우 귀무가설 기각
유의수준 5% : p값이 5% 이하인 경우 귀무가설 기각
유의수준 1% : p값이 1% 이하인 경우 귀무가설 기각
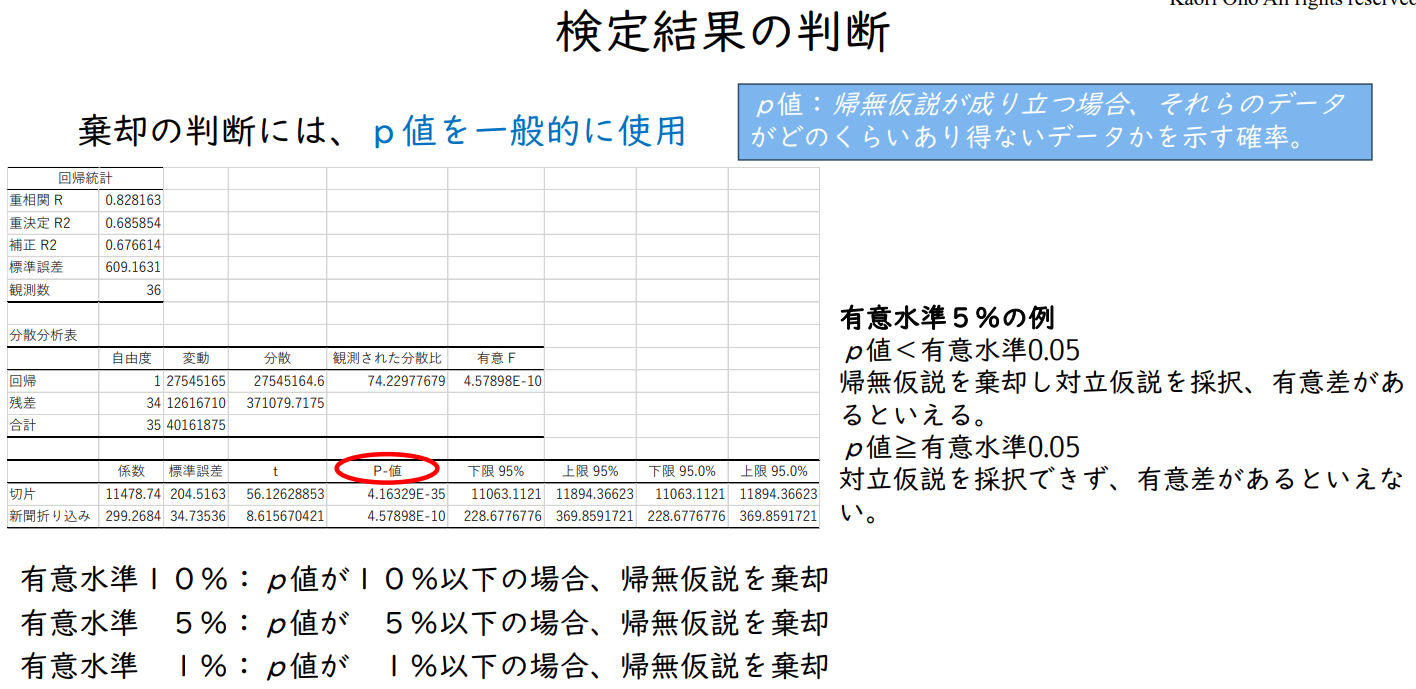
전체강의
다중회귀분석
- 회귀분석의 종류 중 하나
- 설명변수가 2개 이상(종속변수를 설명하는 요인을 가능한 한 많이 모형에 넣는 것)
- 자유도 수정된 결정계수 사용
- F검정 사용

다중선형회귀모형
Yᵢ = a + b₁ X₁ᵢ + b₂ X₂ᵢ + ... uᵢ
a : 상수항
b₁, b₂ : 변수 X₁, X₂의 계수
계수의 추정치는 단회귀분석과 마찬가지로 최소자승법을 사용하여 구한다.
해석은 단회귀분석과 동일

설명변수의 타당성 확인 : t검정
계수: a = 0, b1 = 0, b2 = 0
1. 귀무가설 설정
귀무가설 H0 : b1 = 0
대립가설 H1 : b1≠ 0
2. 각 계수의 t값을 계산한다(소프트웨어로 계산).
t값의 절대값이 1.96보다 크다.
→ 「b는 0이다」라는 귀무가설 H0을 유의수준 5%로 기각
= 변수 X의 계수 b는 유의수준 5%에서 통계적으로 유의하다.

임대료 = 38,395.93 - 939.36 건평 + 1143.22 전용면적 - 201.87 도보
표준오차 (5,126.9) (176.9) (81.9) (390.7)
- 건축연수가 1년 증가하면 임대료가 939엔 낮아진다.
계수 검증
귀무가설 b₁ = 0
t값 = 계수 / 표준오차 = 939.36 / 176.9 = 5.3 → 1.96보다 커서 5% 수준에서 귀무가설 기각 - 전용면적이 1㎡ 증가하면 임대료가 1,143엔 오른다.
계수 검증
귀무가설 b₂ = 0
t값 = 계수 / 표준오차 = 1143.22 / 81.9 = 13.96 → 1.96보다 크므로 5% 수준에서 귀무가설 기각 - 도보가 1분 증가하면 임대료가 202엔 하락한다.
계수 검증
귀무가설 b₃ = 0
t값 = 계수 / 표준오차 = 201.87 / 390.7 = 0.52 → 1.96보다 작으므로 5% 수준에서 귀무가설을 기각할 수 없다.

결정계수: 자유도 수정 결정계수
결정계수 R²의 단점
설명변수를 늘릴수록 1에 가까워진다.
설명변수가 늘어난 만큼을 고려하여 결정계수를 수정: 자유도 수정 결정계수(Adjusted R²)
결정계수 = 1 - [ 관측치와 예측치 사이에 남아있는 차이(잔차) ]
자유도 조정 결정계수 = 1 - [관측치와 예측치 사이에 남아있는 차이(잔차)] ✕ [설명변수의 개수]
자유도 수정 결정계수 < 결정계수
자유도 수정 결정계수는 마이너스가 될 수 있음

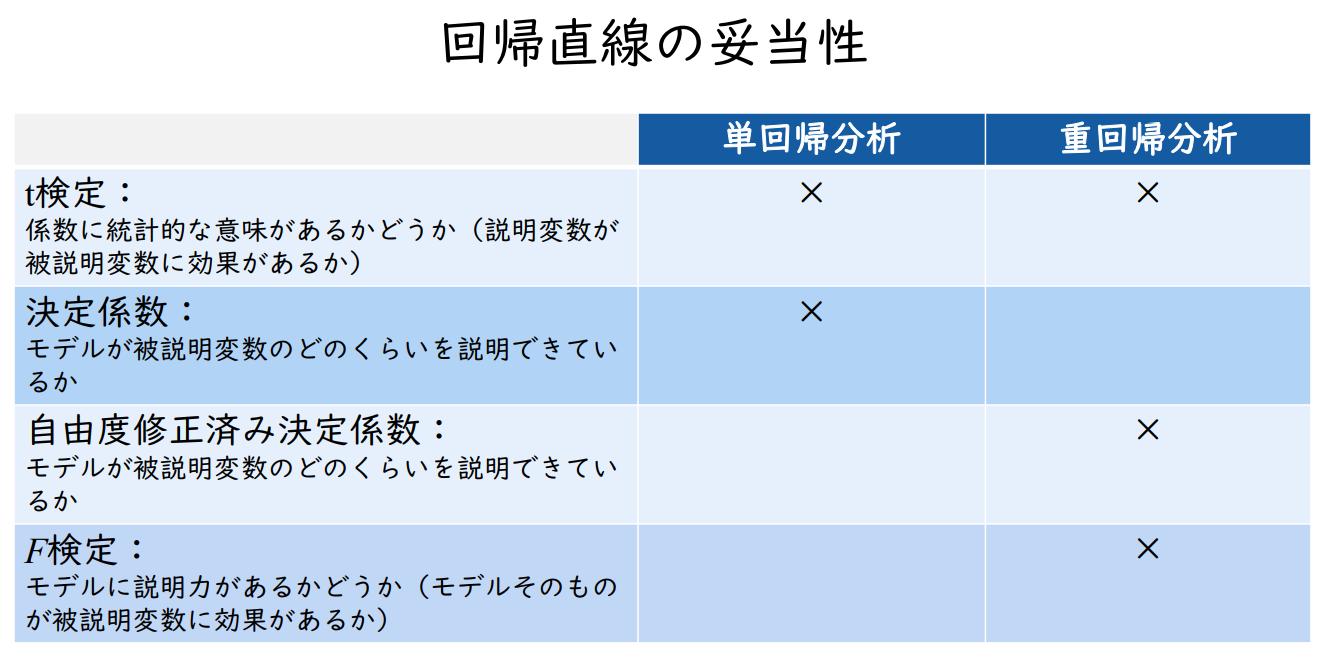
회귀 직선의 타당성
| 단회귀분석 | 중회귀분석 | |
| t 검정: 계수에 통계적 의미가 있는지 여부(설명변수가 피설명변수에 영향을 미치는지 여부) |
X | X |
| 결정 계수: 모델이 피설명변수를 얼마나 잘 설명할 수 있는가? |
X | |
| 자유도 보정 결정계수: 모형이 피설명변수를 얼마나 잘 설명할 수 있는가? |
X | |
| F 검정: 모델에 설명력이 있는지 여부(모델 자체가 피설명변수에 영향을 미치는지 여부) |
X |
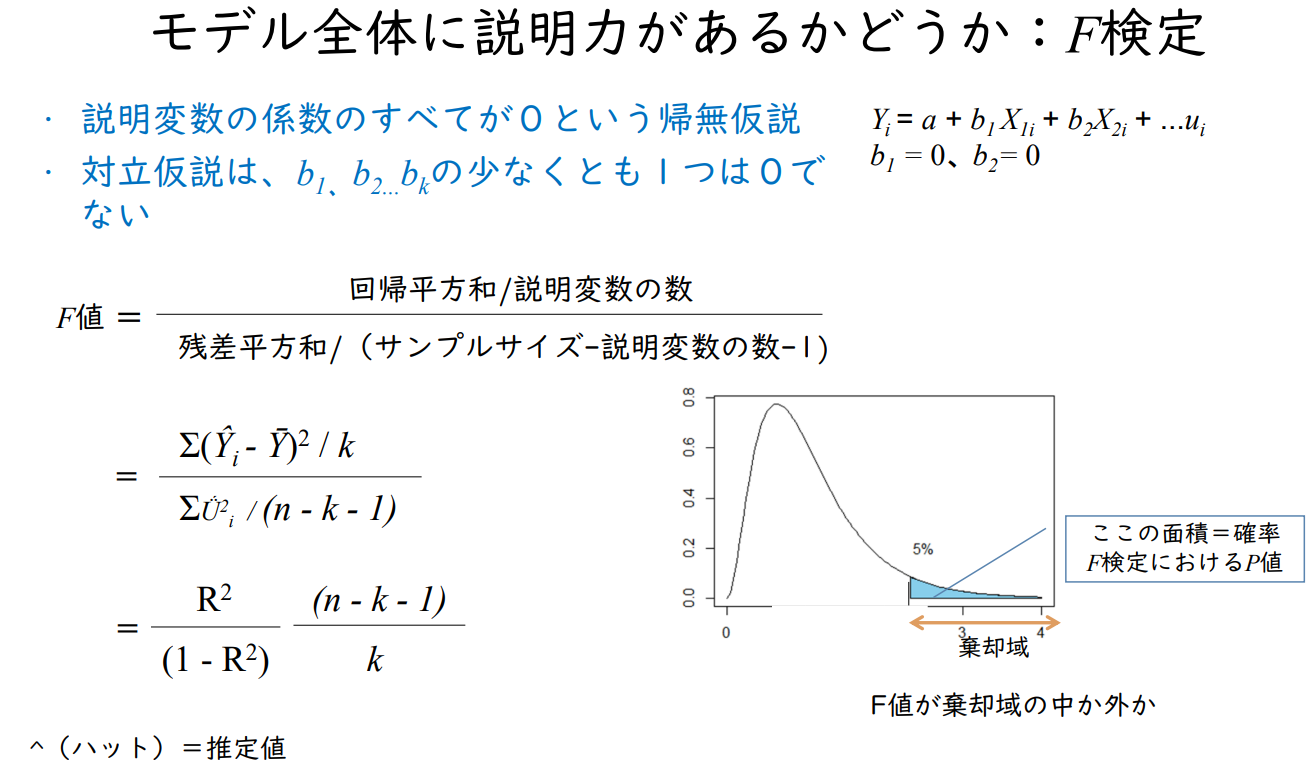
모델 전체에 설명력이 있는지 여부 : F검정
- 설명변수의 계수가 모두 0 이라는 귀무가설
- 대립가설은 b₁, b₂ .... bₖ 중 하나 이상은 0이 아니다.
Yᵢ = a + b₁ X₁ᵢ + b₂ X₂ᵢ + ... uᵢ
b₁ = 0, b₂ = 0
엑셀 작업
데이터 탭 → 데이터 분석
'회귀분석' 선택
입력 Y와 X
라벨 선택
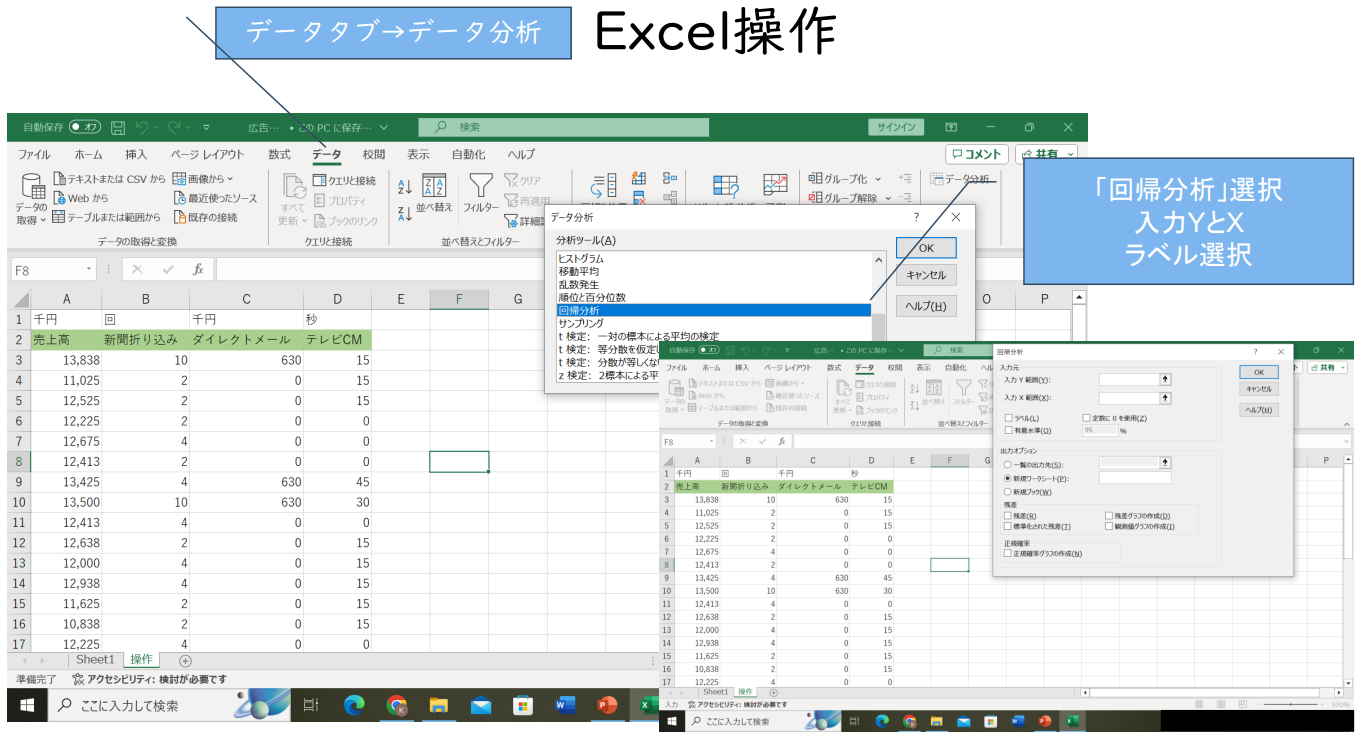
라벨
잔차
표준화된 잔차
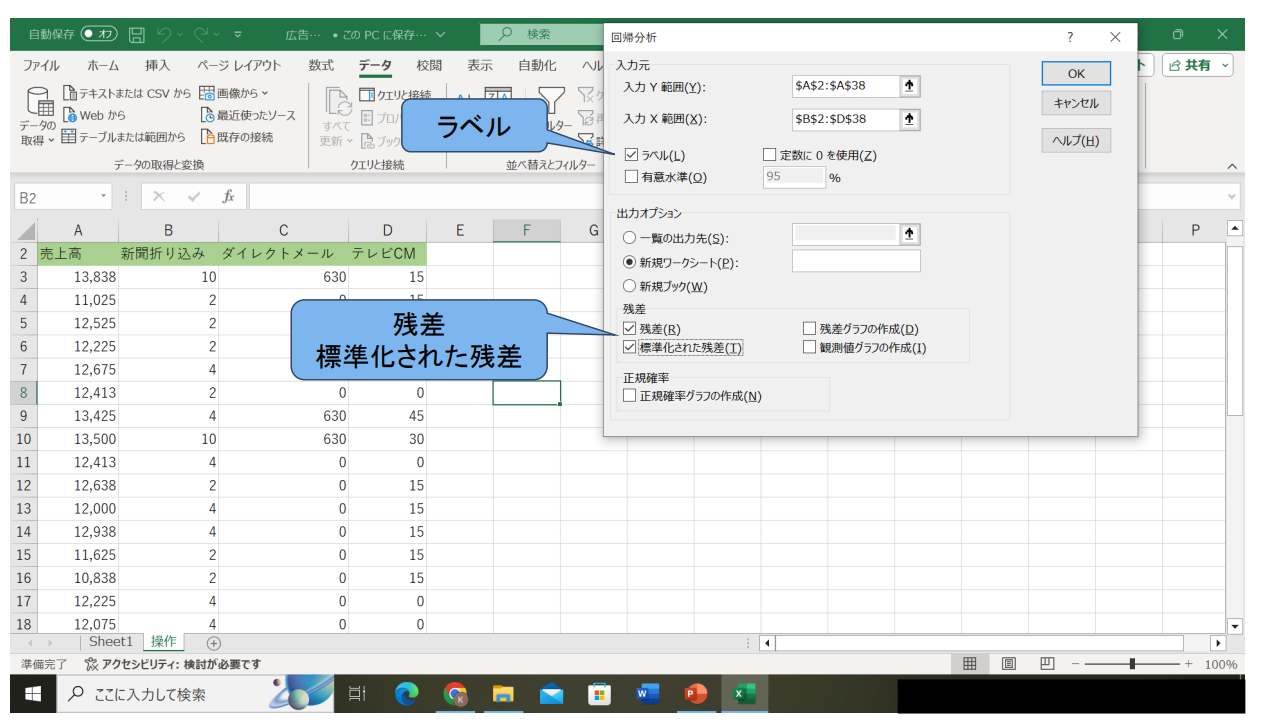
예: 광고와 매출
매출 = a + b₁ 신문광고 + b₂ 다이렉트 메일 + b₃ TV CM ... u
주목해야 할 항목
✓ 계수
✓ 회귀 통계
✓ P값
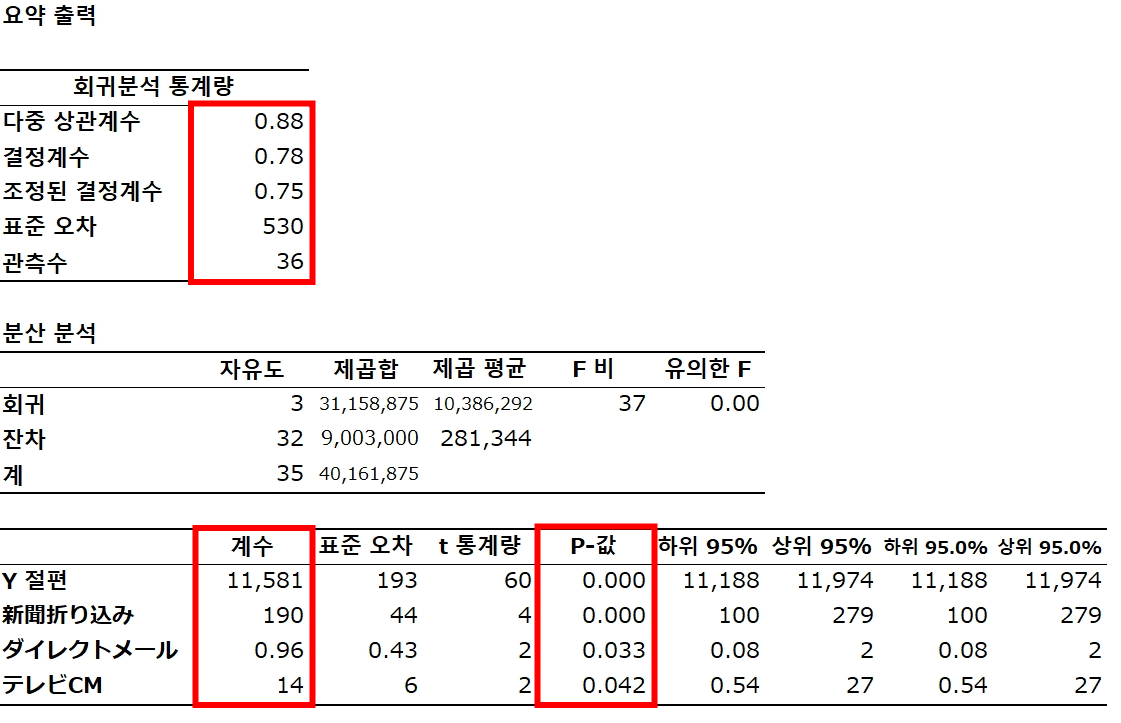
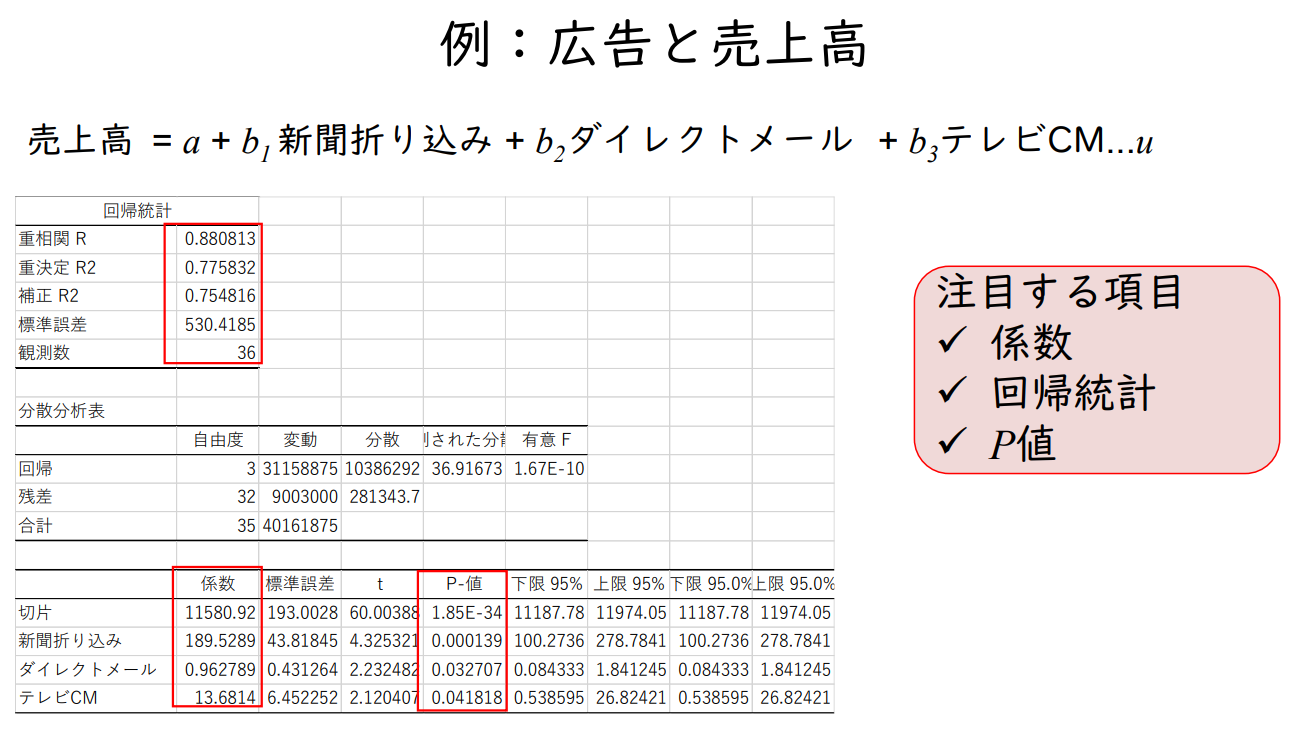
✓ 계수의 부호가 플러스인지 마이너스인지 여부
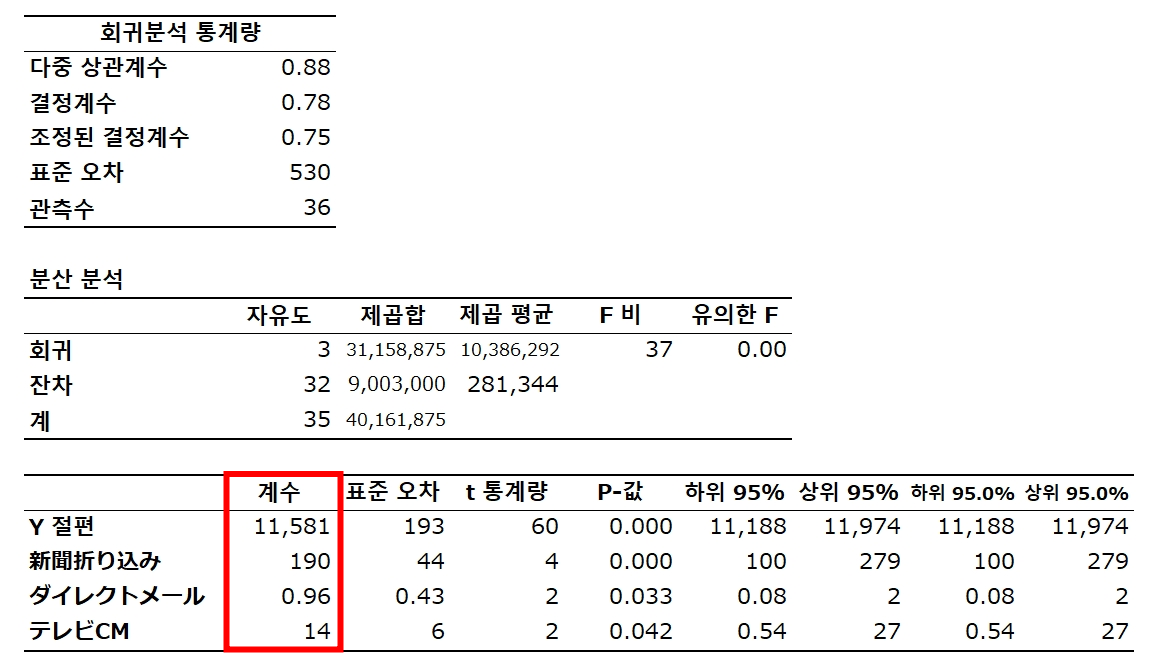
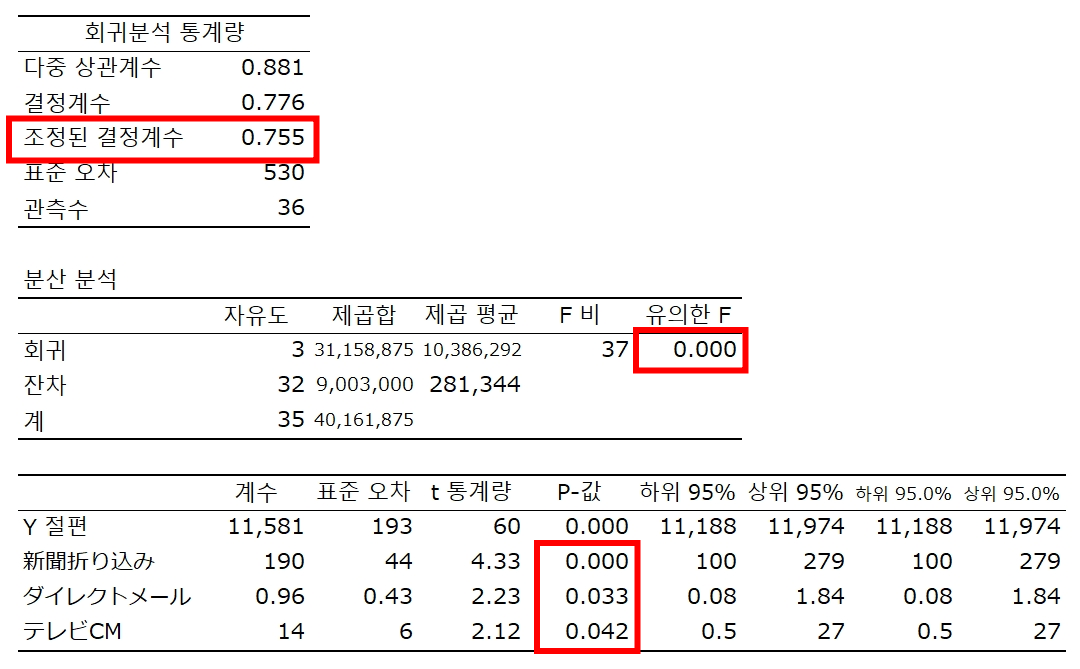
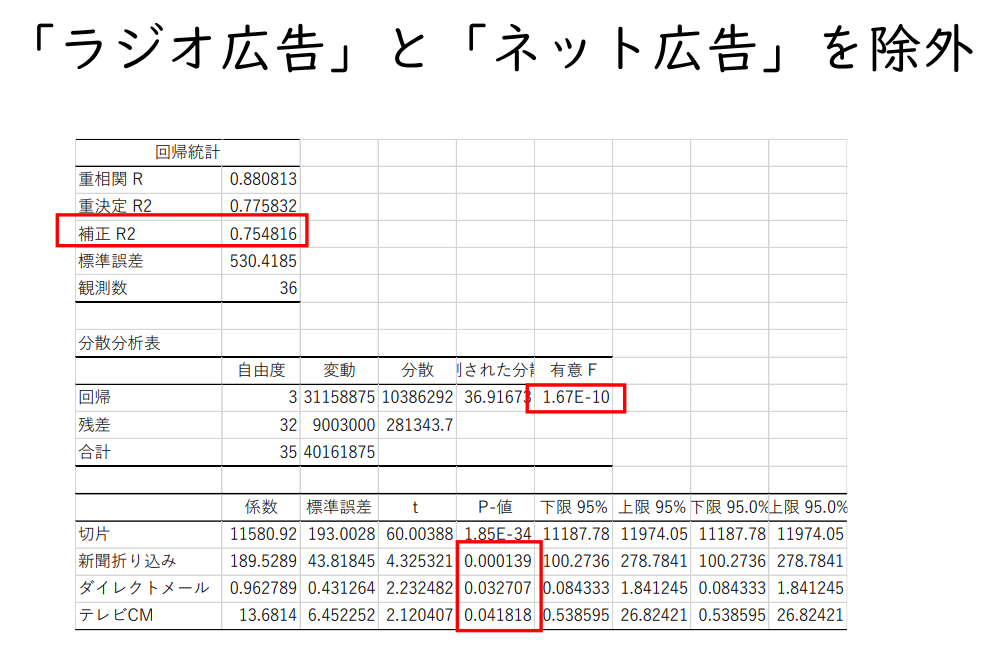
판매 = 11,581 + 190 신문 + 0.96 다이렉트메일 + 14 TV CM
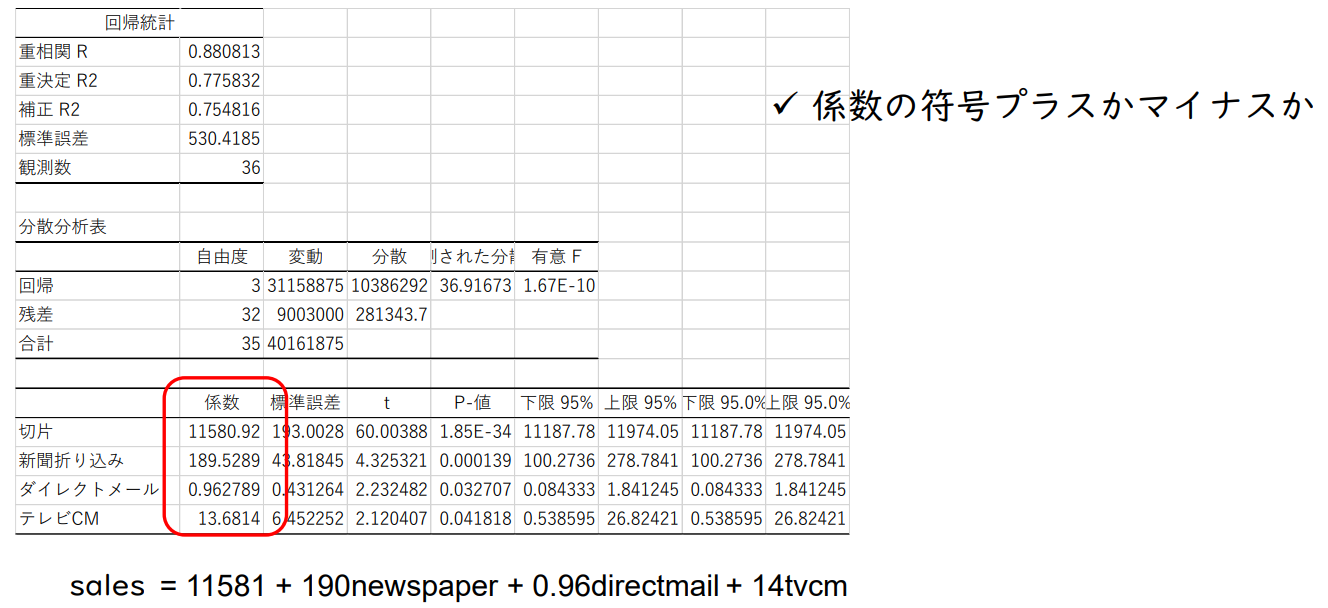
✓ 계수에 의미가 있는지 여부 → P 값
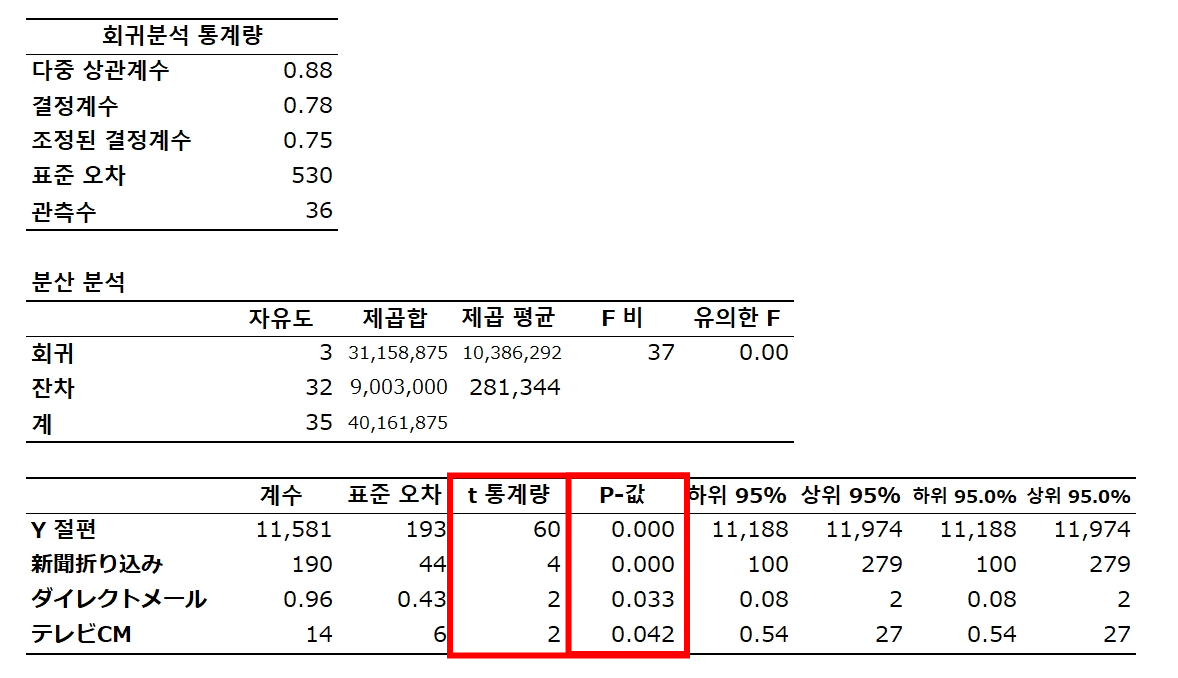
t값 = 계수의 추정치 / 계수의 표준오차
신문광고 190 / 44 = 4.3
신문광고 P값 = 0.000139282 매우 작은 값
⇒ 유의수준이 10%, 5%, 1%이면 유의하다,
귀무가설 H₀ : b₁ = 0 은 기각할 수 있다.
1.84909E-34 = 1.84909 x (0.1)⁸
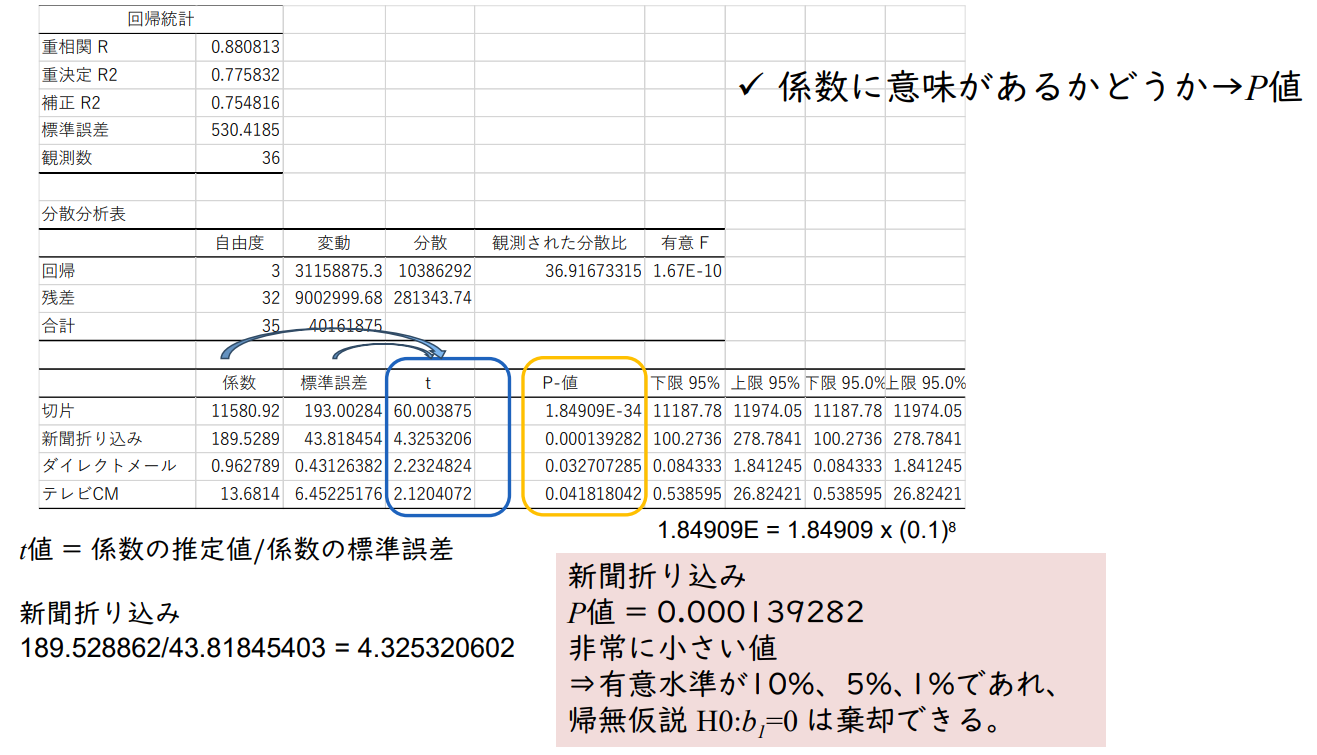
✓ 모델이 얼마나 많은 것을 설명하는지
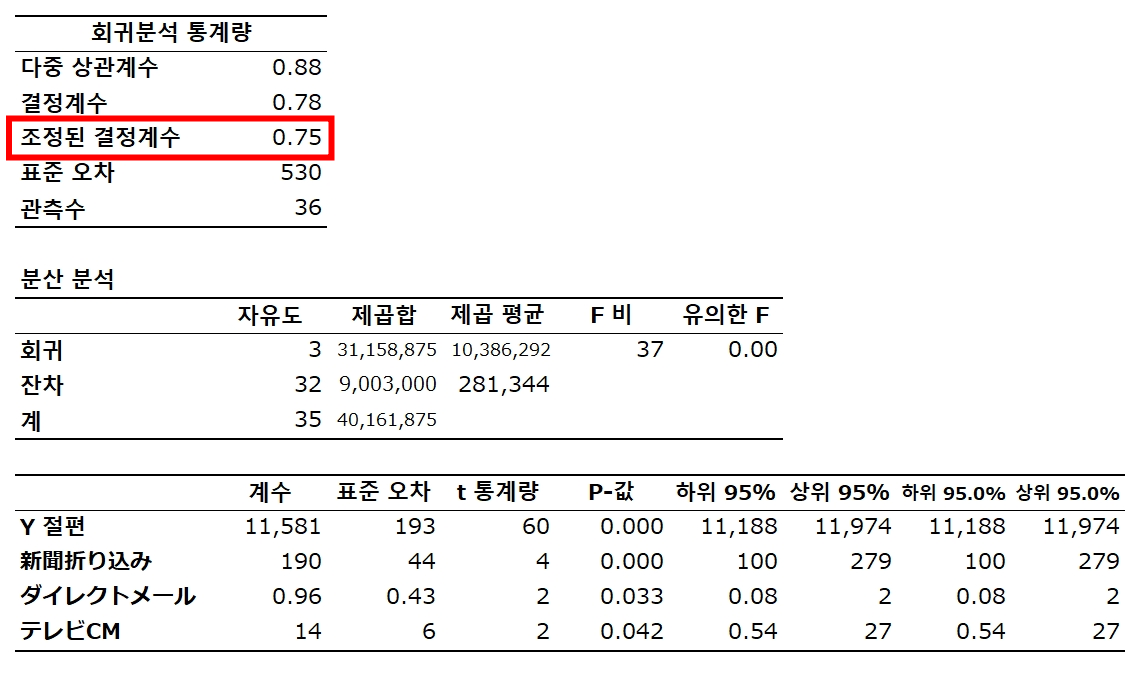
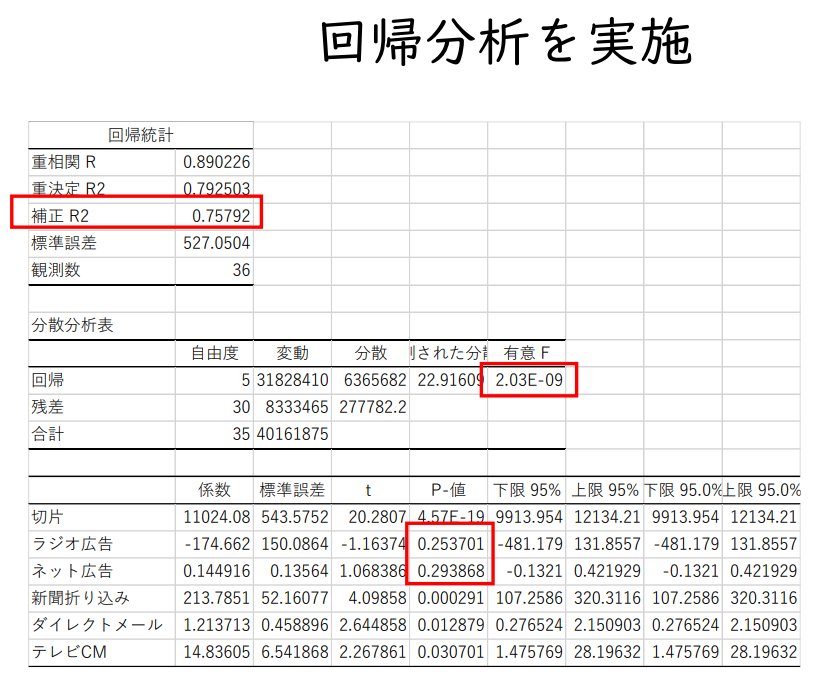
설명변수가 2개 이상이므로 자유도 보정 결정계수 사용
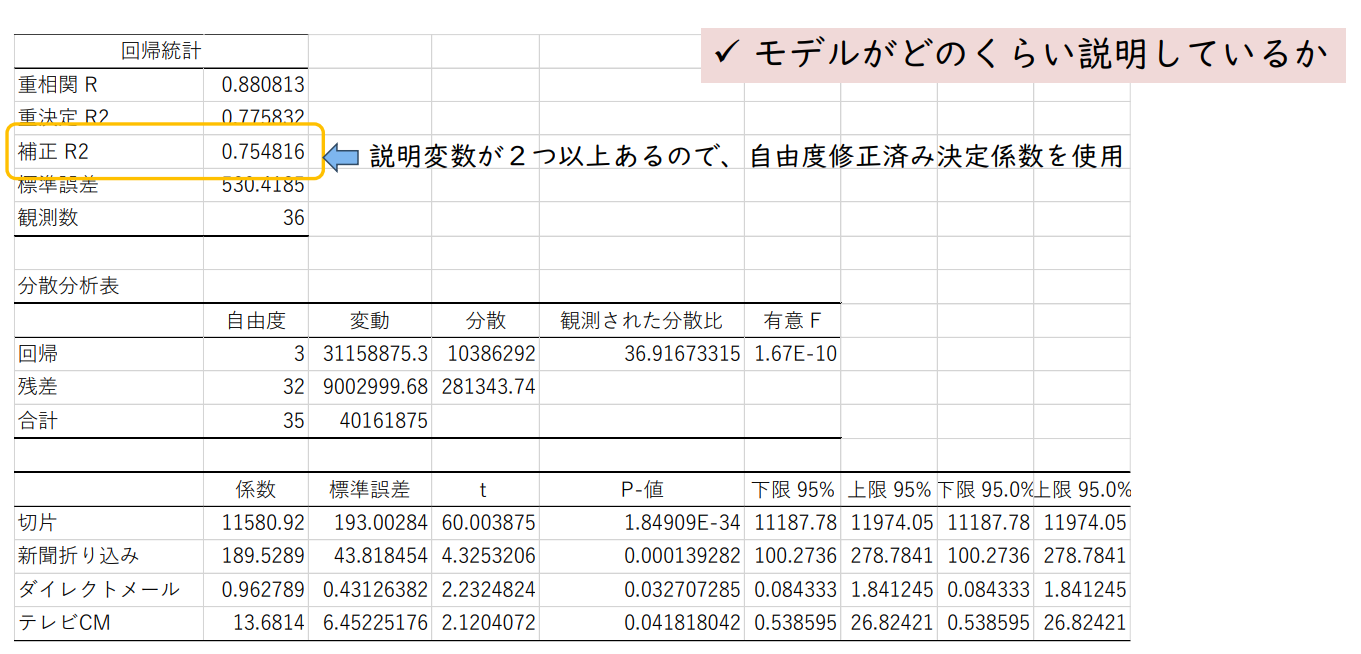
R² = 회귀제곱합 / 전체 변동
31,158,875 / 40,161,875 = 0.7758
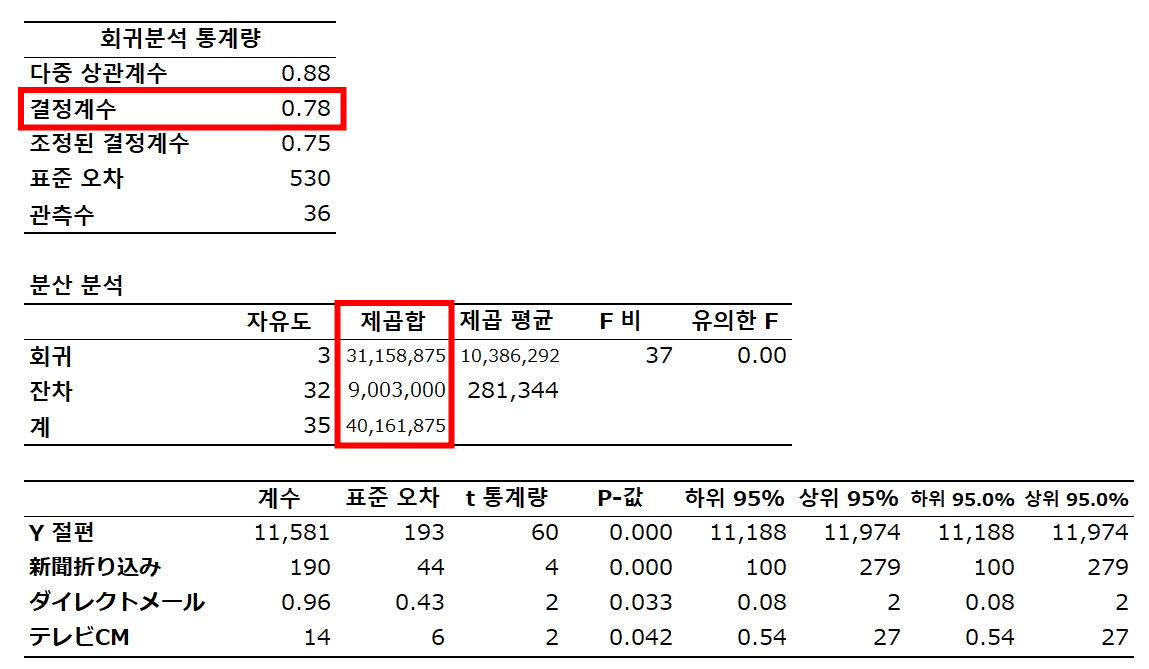
전체 변동 = 관측값 - 평균값 = 편차 = Σ(Yi- Ȳ)²
회귀 제곱합 = 예측값 - 평균값 = Σ(Ŷi- Ȳ)²
잔차 제곱합 = 관측치 - 예측치 = Σ(Yi- Ŷi)²
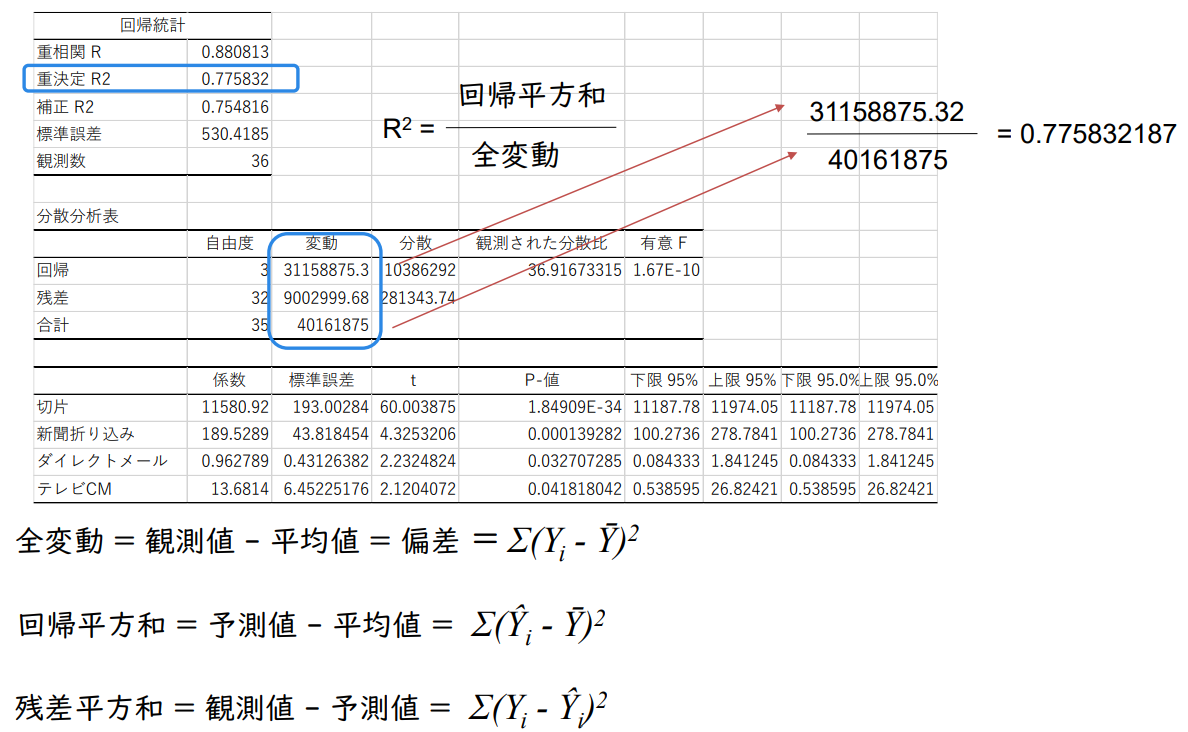
R² = 회귀제곱합 / 전체 변동
31,158,875 / 40,161,875 = 0.7758
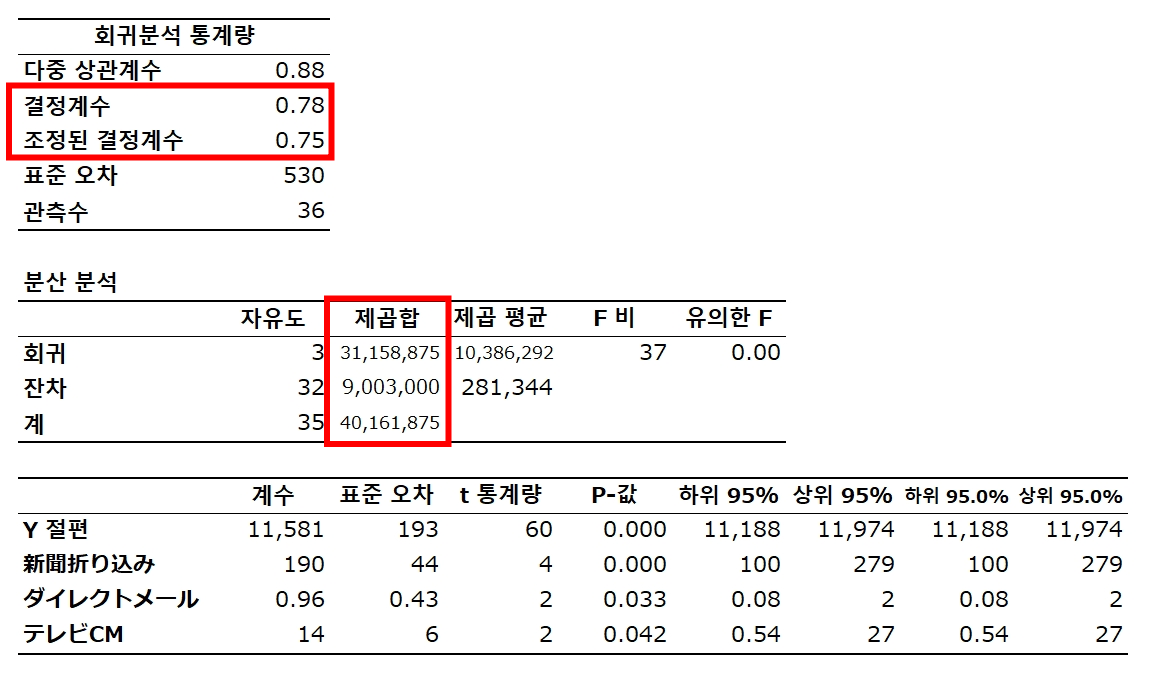
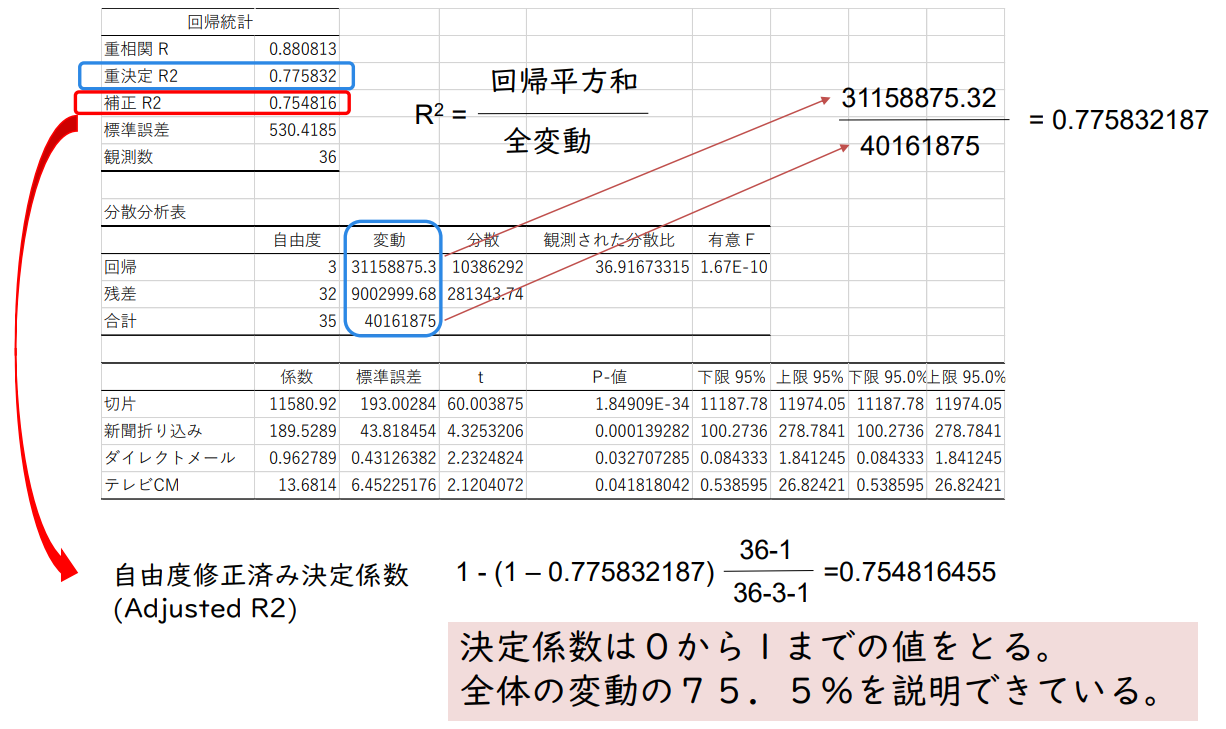
자유도 보정 결정계수(Adjusted R2) 1 - ( 1 - 0.775832187 ) { ( 36 - 1 ) / ( 36 - 3 - 1 ) } = 0.7548
결정계수는 0에서 1까지의 값을 취한다.
전체 변동의 75.5%를 설명할 수 있다.
✓ 모델 전체의 설명력
모든 설명 변수의 계수가 0이라는 귀무가설 검증
F값 : F비
F검정에 기반한 P값 : 유의한 F
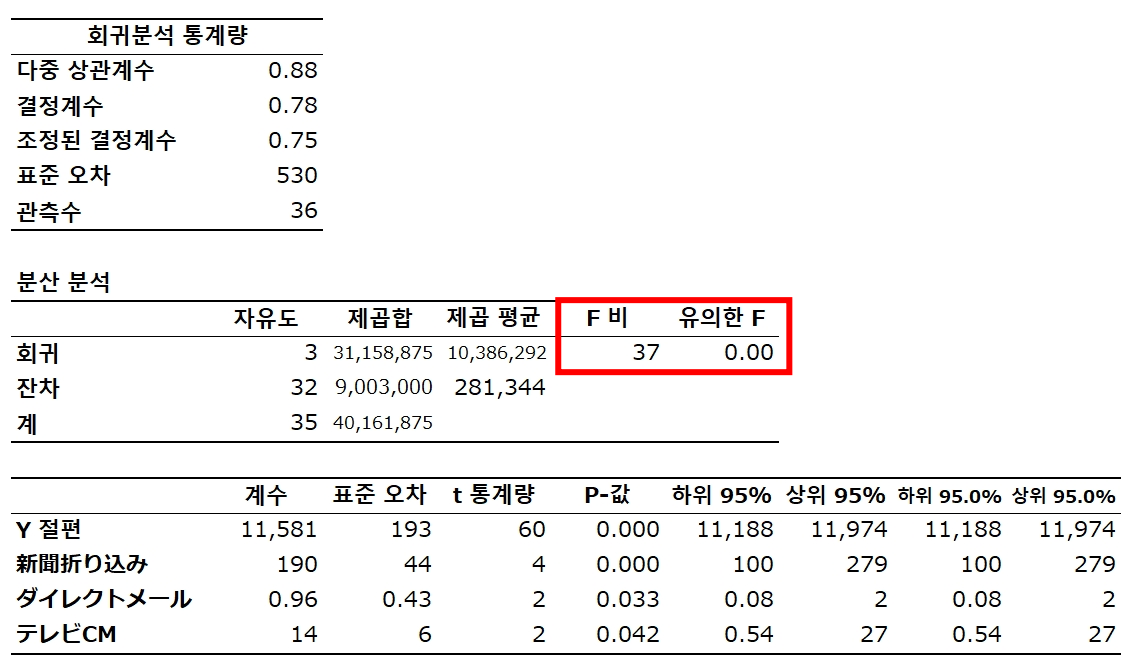
F의 유의수준이 매우 작다.
모든 설명변수의 계수가 0이라는 귀무가설을 유의수준 1%에서 기각

단회귀분석의 경우 t값과 p값
유의한 F값은 P값과 일치
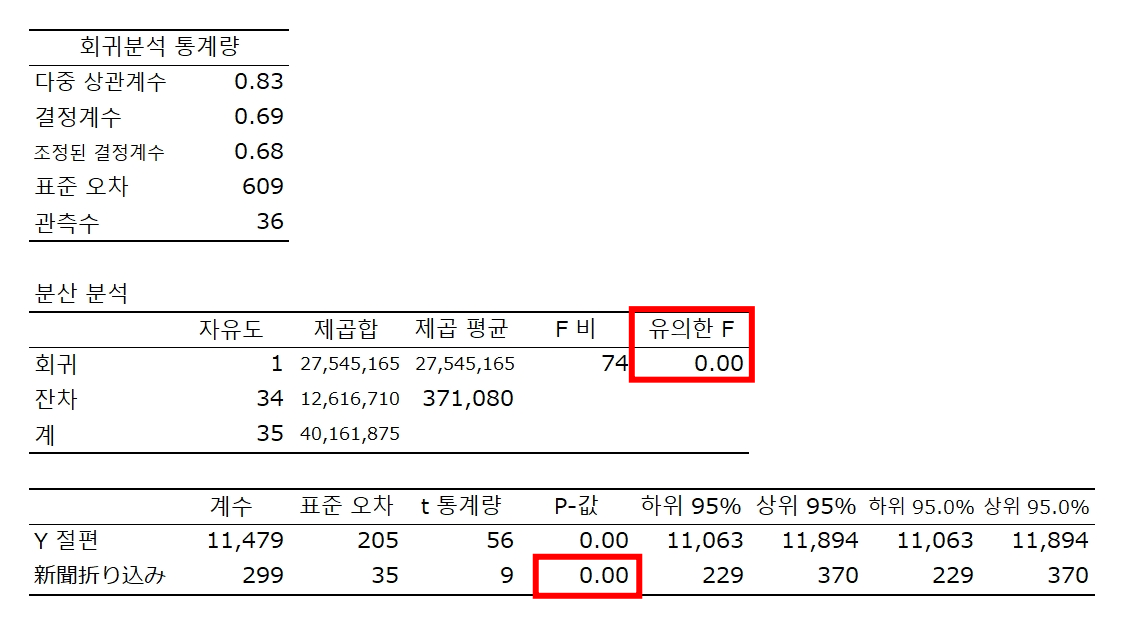
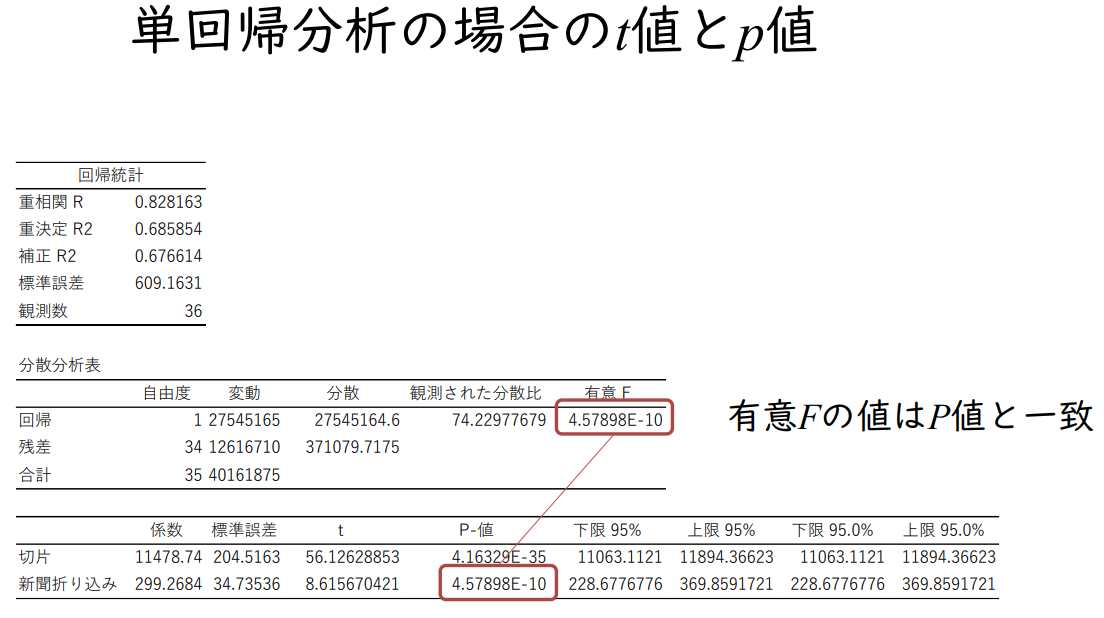
요약
- t값은 각 설명변수가 피설명변수에 미치는 영향의 크기를 나타내는 지표
(t값이 클수록 피설명변수에 미치는 영향이 강함). - P값은 각 설명변수가 피설명변수와 관계가 있는지를 나타내는 확률
(P값이 0.05 미만이면 해당 설명변수는 피설명변수와 '관계가 있다'고 할 수 있고,
0.05 이상이면 '관계가 없다'고 볼 수 있다). - F값은 모델 전체에 설명력이 있는지 여부를 나타내는 지표.
- P값은 다양한 t값 또는 F값에 대해 그 오른쪽 면적이 전체에서 차지하는 비율을 표시한다.
- P값이 작을수록 우변의 면적(기각 영역의 면적)이 작아져 귀무가설을 기각할 수 있는 가능성이 높아진다.
- t값이 클수록 귀무가설을 기각할 수 있는 가능성이 높아진다.
| t값 | P값 | F값 |
| 각 설명변수가 피설명변수에 미치는 영향의 크기를 나타내는 지표 | 각 설명변수가 피설명변수와 관계가 있는지를 나타내는 확률 | 모델 전체에 설명력이 있는지 여부를 나타내는 지표 |
| t값이 클수록 피설명변수에 미치는 영향이 강함 |
P값이 0.05 미만이면 해당 설명변수는 피설명변수와 '관계가 있다'고 할 수 있고, 0.05 이상이면 '관계가 없다'고 볼 수 있다 |
|
| 다양한 t값 또는 F값에 대해 그 오른쪽 면적이 전체에서 차지하는 비율을 표시한다 | ||
| 클수록 귀무가설을 기각할 수 있는 가능성이 높아진다. |
작을수록 우변의 면적(기각 영역의 면적)이 작아져 귀무가설을 기각할 수 있는 가능성이 높아진다. |

논문에서 분석 결과 기재 방법
분석 도구의 결과를 그대로 복사하여 붙여 넣지 않는다.
① 직원 변화 = a₁ + b₁ 매출액 변화 + b₂ ROA + u
② 직원 변화 = a₂ + b₃ 매출액 변화 + v
계수와 표준오차 또는 t값을 세로로 나열한다.
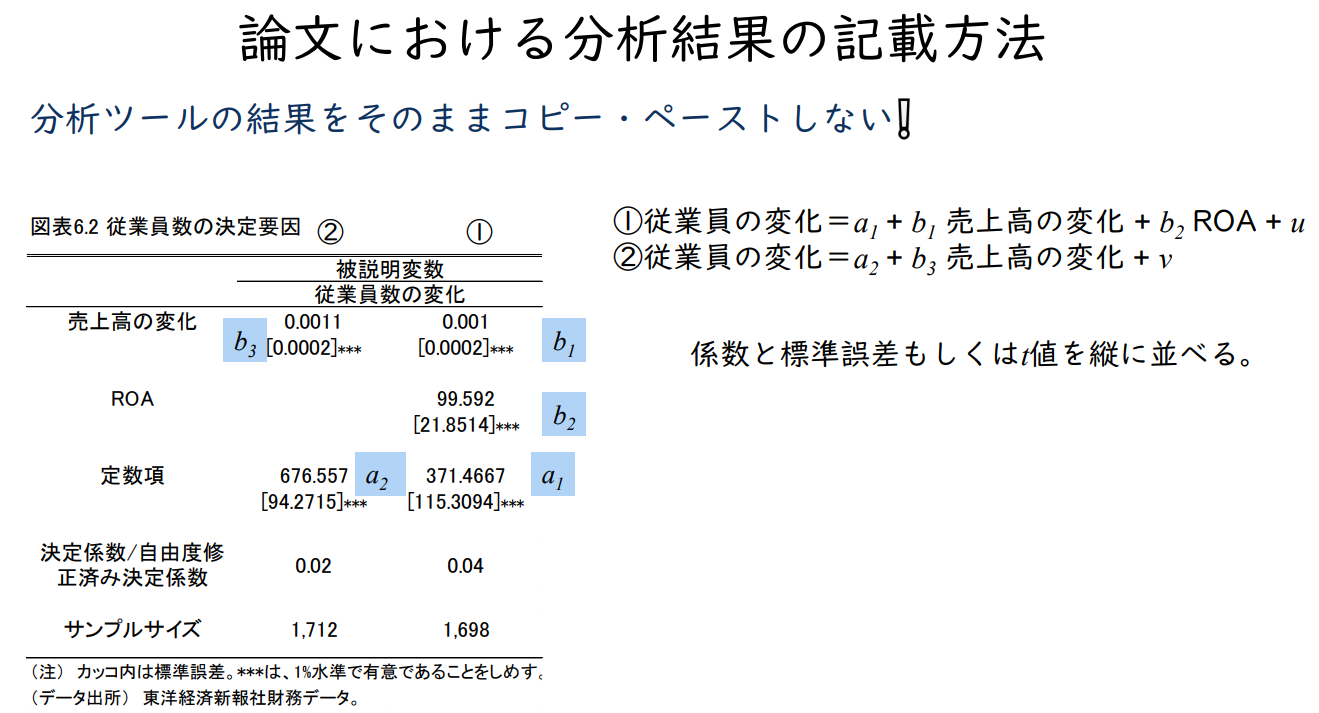
논문 형식 확인
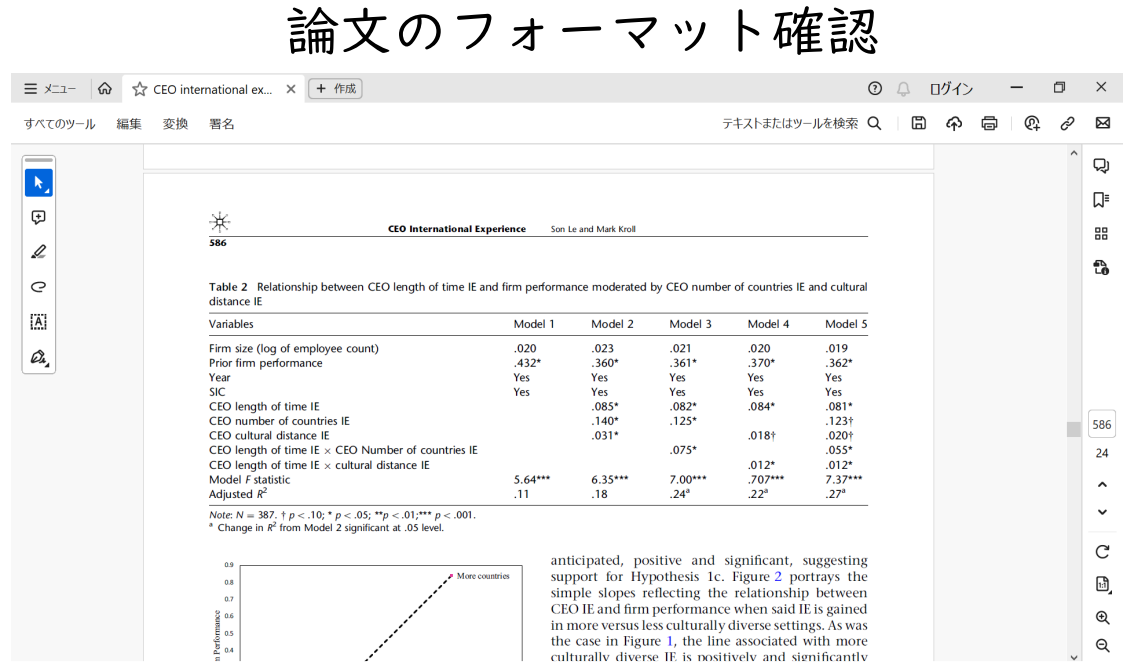
연습문제 : 기업의 해외진출과 환율의 관계
엔고로 인해 기업의 해외진출이 증가한다.
- '환율.csv' 파일을 이용하여 환율이 해외직접투자에 미치는 영향을 엑셀 등으로 분석해보자.
- 엔고일 때 기업의 해외 진출이 많다고 봐도 될까요?

엔고에서는 환율의 수치가 작아진다.
직접투자 (Y) = 14,918 - 82.67 환율(X)
표준오차 (2,320) (21.22)
R² = 0.06
p값의 유의수준은 매우 작다.
모든 설명변수의 계수가 0이라는 귀무가설은 유의수준 1%에서 기각
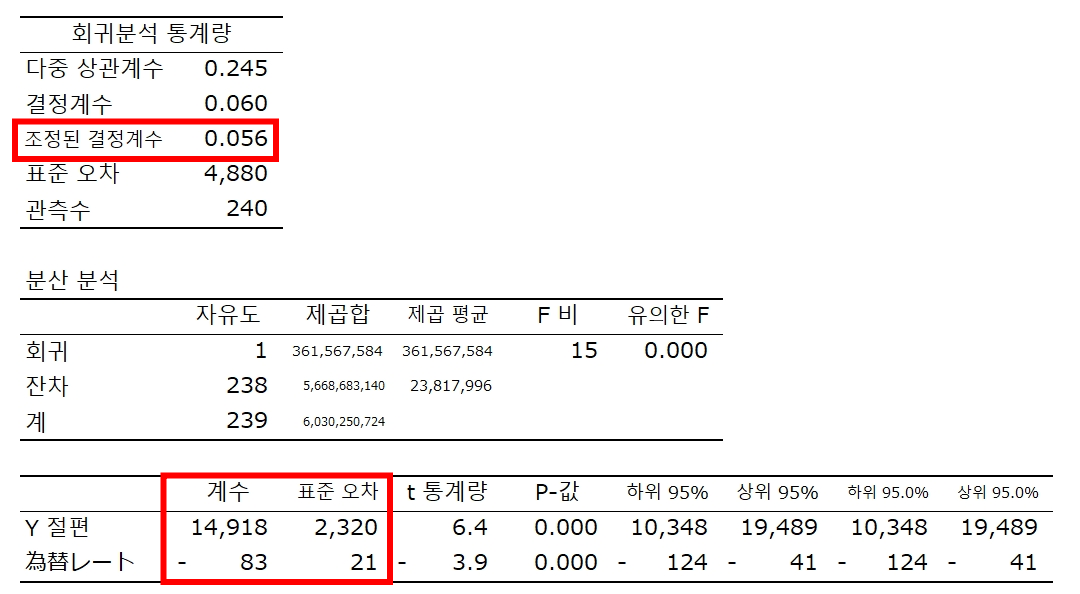
환율의 계수가 마이너스 → 환율 수치가 작아진다.
따라서 환율이 엔고일수록 해외직접투자가 많아진다.

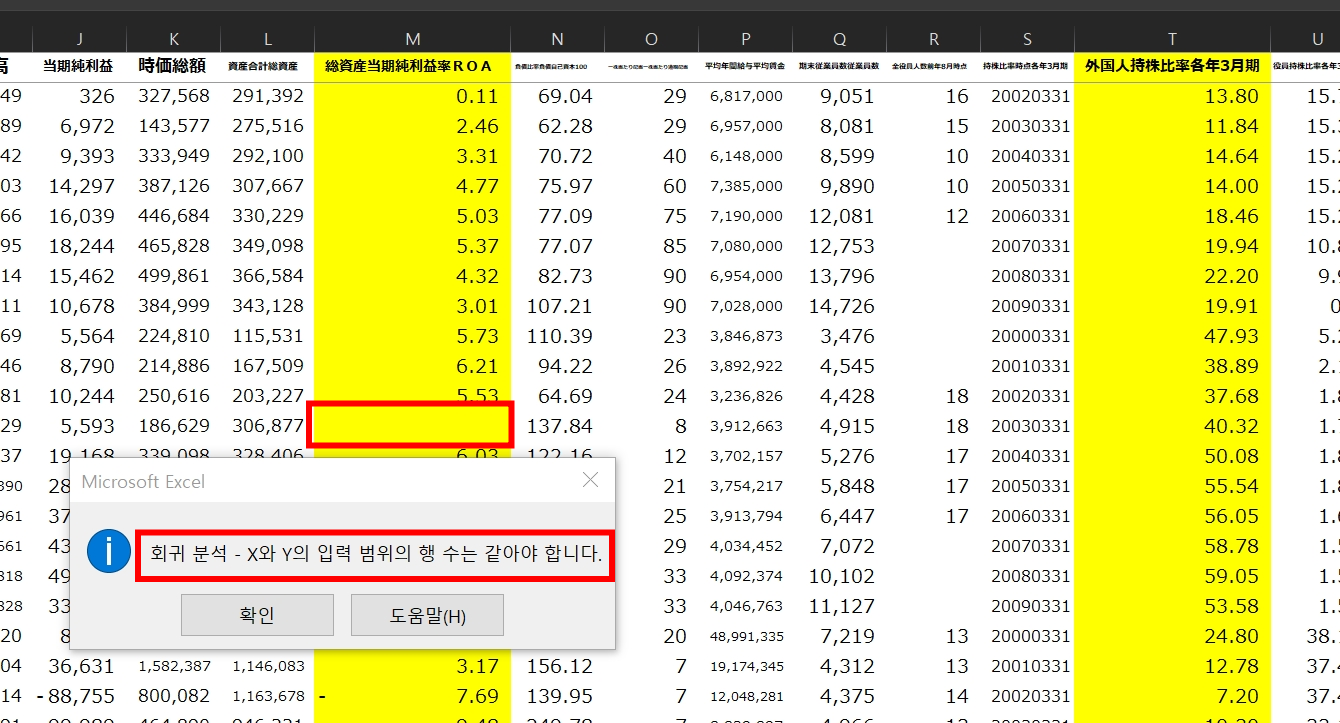
연습 2 : 외국인 지분율과 ROA의 영향
'financial_analysis.csv.' 파일의 데이터를 이용하여 외국인 지분율과 ROA의 영향을 분석해 보세요.
- 다음 두 공식을 엑셀 등을 이용하여 측정하여 하나의 표로 정리해 주세요.
- 결과에 대해 간략하게 설명해 주세요.
참고로 u와 v는 오차항입니다.
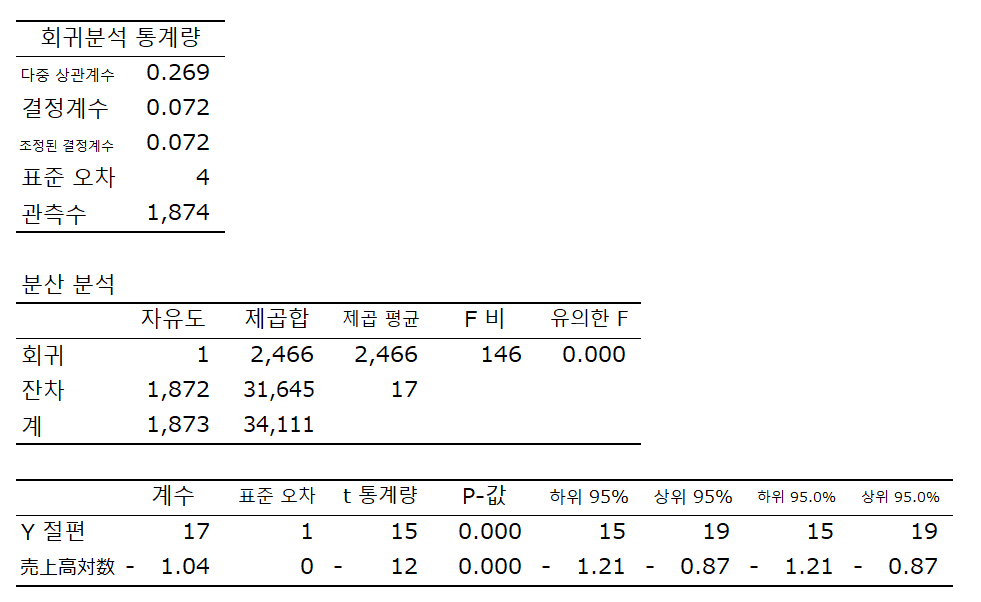
(1) ROA = a₁ + b₁ 매출액 대 수치 + u
(2) ROA = a₂ + b₂ 매출액 대비 수치 + b₃ 외국인 지분율 + v
* 대수(log) 변환은 대수 정규분포(오른쪽으로 치우친 분포)를 정규분포에 가깝게 하기 위해 사용하는 방법

(1) ROA = 17.14 - 1.04 매출액대수치 + u
(2) ROA = 16.02 - 1.15 매출액대수치 + 0.12 외국인지분비율 + v

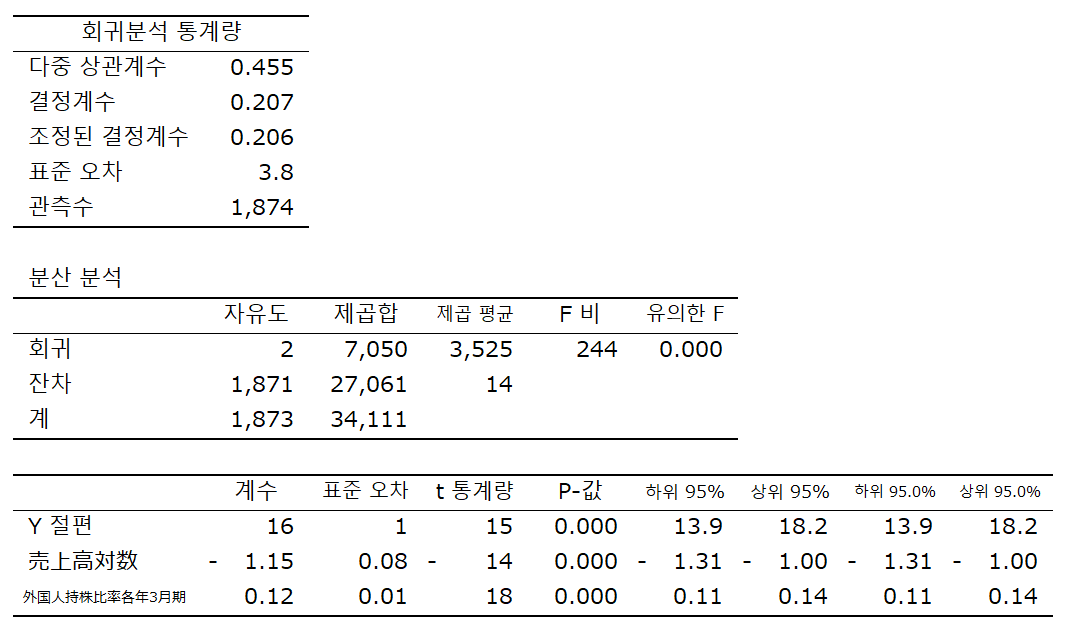
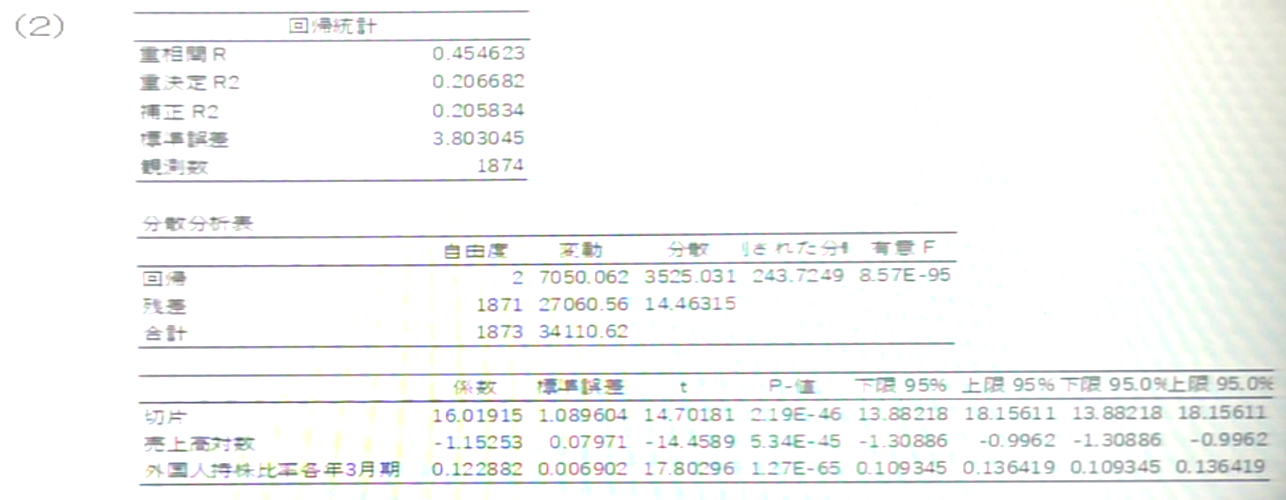
매출액 대수, 외국인 지분율 모두 유의수준 1%에서 유의


의문
설명변수를 많이 넣으면 목적을 더 자세히 설명할 수 있을 것이라고 생각할 수 있을까?
다중회귀분석의 회귀식 가정
설명변수 X1 ~ Xn은 별개의 요인으로 서로 연관성이 없다.
설명변수들 사이에 높은 연관성이 있다 : 다중공선성 Multi-Collinearity(다중공선성)

다중공선성 가능성
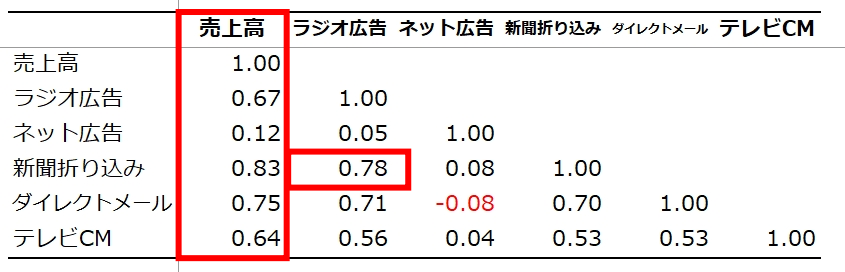
- 상관계수가 0.9 이상
- 요인은 양(음)의 상관관계로 보는 것이 타당함에도 불구하고, 계수의 부호가 반전되어 있다.
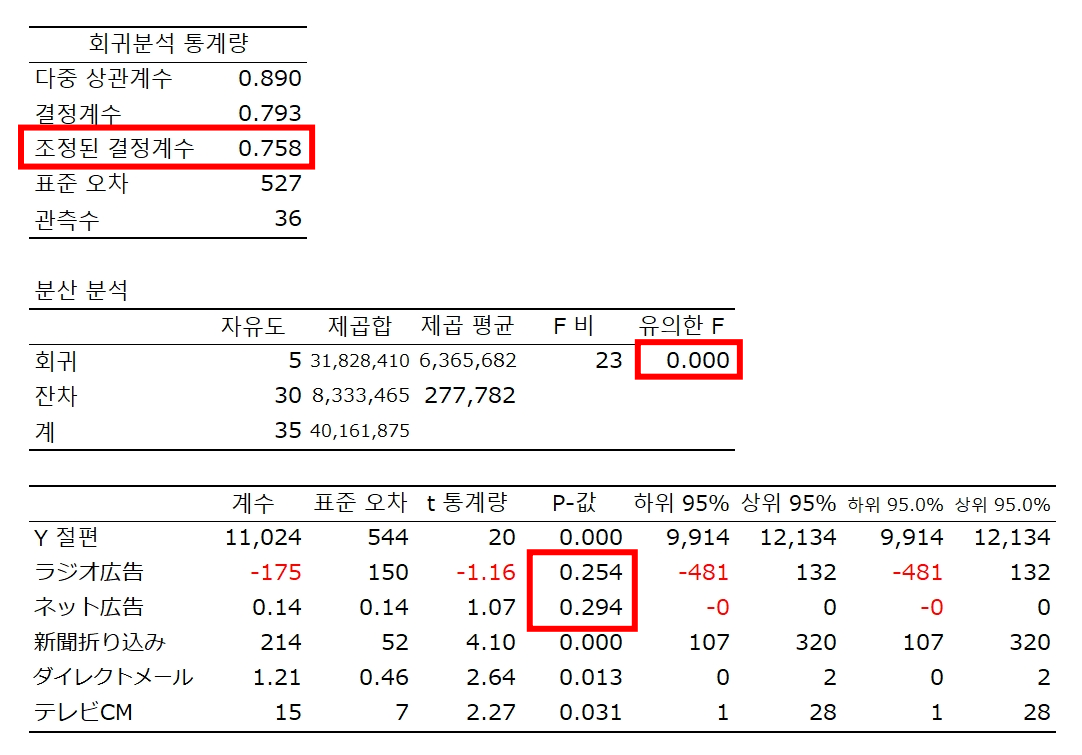
- 자유도 보정된 결정계수가 양호한 결과임에도 불구하고 t값이 너무 작다.
- 가용할 수 있어야 할 설명변수의 p값이 5%를 초과하는 경우

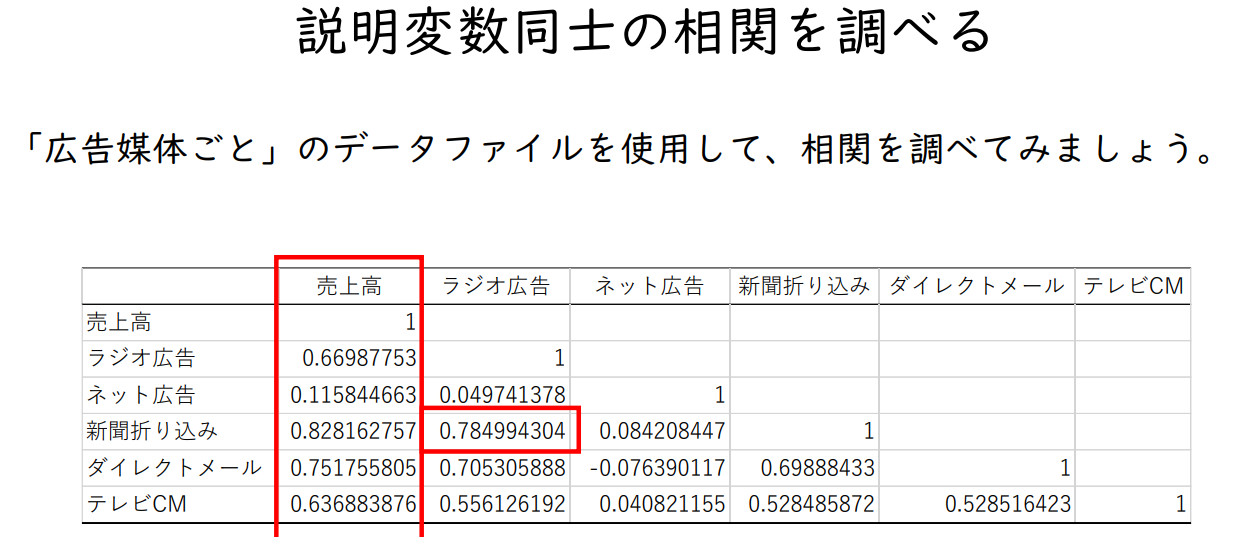
설명변수 간의 상관관계 알아보기
'광고 매체별' 데이터 파일을 사용하여 상관관계를 조사해 봅시다.
회귀분석 실시
'라디오 광고'와 '인터넷 광고' 제외
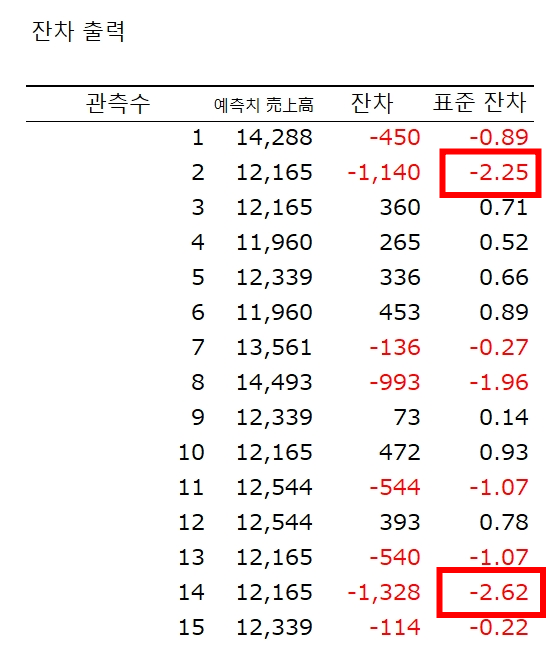
표준편차로 이상치 확인
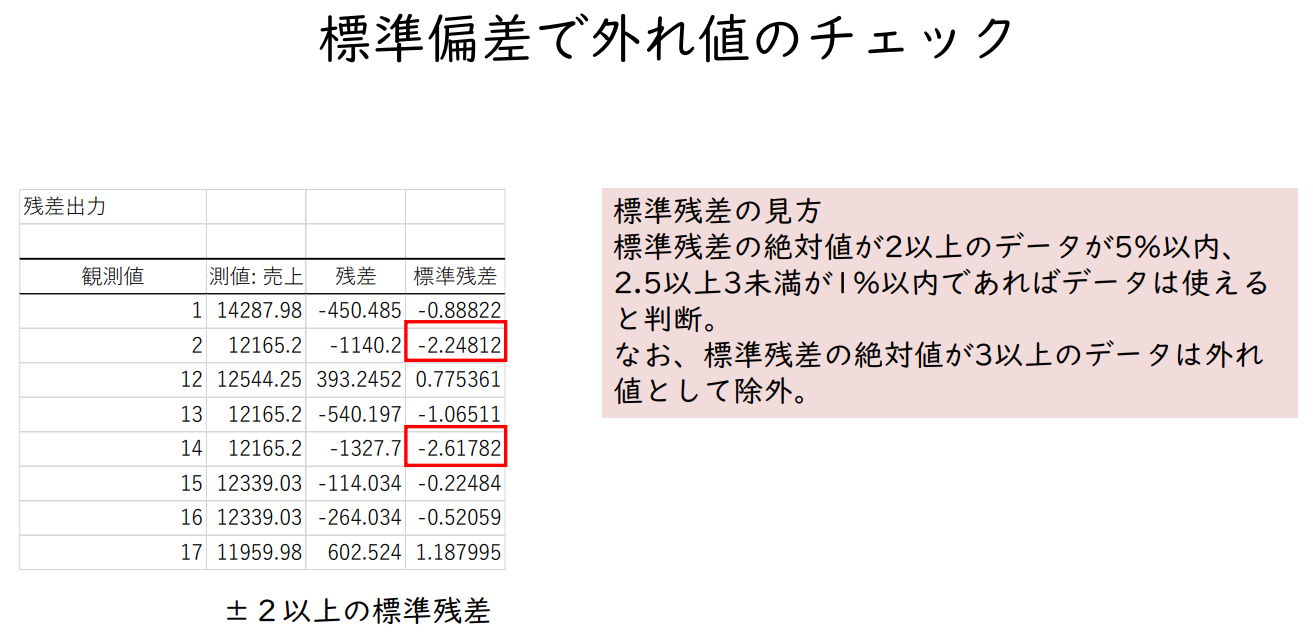
표준편차 보는 법
표준잔차의 절대값이 2 이상인 데이터가 5% 이내, 2.5 이상 3 미만이 1% 이내이면
데이터를 사용할 수 있다고 판단.
표준잔차의 절대값이 3 이상인 데이터는 이상값으로 제외한다.
±2 이상의 표준 잔차
예측치 구하기
매출 예측치 = 11,581 + 190 x 신문광고(회) + 0.96 x 다이렉트 메일(천엔) + 14 x TV광고(초)
예를 들면,
신문광고를 10회, 다이렉트 메일은 500,000엔, TV광고는 15초라고 가정하면, 매출 예측치는 다음과 같다,
매출 예측치 = 11,581 + 190 x 10 + 0.96 x 500 + 14 x 15 = 14,163천엔

연습 3
회귀분석을 통해 가설을 검증해 봅시다.
가설
에너지 소비량은 그 나라의 부의 정도에 따라 결정되지 않을까?
데이터 정부 통계
- 국내총생산(GDP)
- 1인당 에너지 소비량
설명변수를 추가해 보자.

'WBS - 2023 Winter > 기업 데이터 분석' 카테고리의 다른 글
| (기업데이터 #13-14) 패널데이터, 회귀분석 정리 (0) | 2024.01.27 |
|---|---|
| (기업데이터 #11-12) 더미 변수, 교차항, 로지스틱 회귀 분석 (0) | 2024.01.20 |
| (데이터 #7-8) 연구 방법, 논문 작성 (0) | 2023.12.23 |
| (데이터 #5-6) 데이터 간의 관계 파악 | 상관관계, 인과관계, 단회귀 분석 (0) | 2023.12.16 |
| (데이터 #3-4) 일부 데이터로 전체 추정하기 | 정규분포, 표준정규분포, 확률, 추정과 t검정 (0) | 2023.12.09 |
| (데이터 #1-2) Introduction (0) | 2023.12.04 |



