기업 데이터 분석 가을학기
제13, 14회 패널데이터, 회귀분석 정리
2024년 1월 27일 (토)
상학학술원 비즈니스-파이낸스연구센터 오노 카시오리

연습4 변수 설정
각 가설을 검증할 때 피설명변수와 설명변수가 어떻게 되는지 간단히 설명하시오.
또한 그 결과를 수식으로 표현하시오.
(1) 우리는 주택담보대출이 어떻게 결정되는지 분석하려고 합니다.
은행에 주택담보대출을 신청한 사람의 정보와 주택담보대출을 받을 수 있었는지를 나타내는 데이터가 있다고 가정하자.
이 데이터를 이용하여 여성이 주택담보대출 심사에서 합리적으로 설명할 수 없는 불리한 대우를 받고 있는지 주목하고 있다.
가설 1: 주택담보대출을 신청했을 때 연봉이 낮은 사람은 거절당할 가능성이 높을 것이다.
가설 2: 여성이 남성보다 거절당할 가능성이 높다.
가설 3: 결혼한 사람은 결혼하지 않은 사람보다 거절당할 가능성이 낮다.

연습4 변수 설정 답변
Pr ( Y=1\X) = F ( a + b1 X )
- F는 분포 함수
- Pr ( Y=1 ) : Y가 1을 취할 확률
이항 선택 모델: '한다' 또는 '하지 않는다'
피설명변수: 심사가 통과되면 '1', 통과되지 않으면 '0' → '심사 더미'로 한다.
가설1: 주택담보대출을 신청했을 때, 연봉이 낮은 사람은 거절당할 가능성이 높을 것이다.
설명변수:연소득→ 플러스에서 유의할 것으로 예상한다.
가설2: 여성은 남성보다 거절당할 가능성이 높다.
설명변수: 여성이면 결혼 여부, 남성이면 기혼 여부 → '여성 더미'는 마이너스로 유의할 것으로 예상
가설3: 결혼한 사람은 결혼하지 않은 사람보다 거절당할 가능성이 낮다.
설명변수: 결혼한 경우 결혼 여부, 결혼하지 않은 경우 미혼 여부 → '결혼 더미'가 양(+)으로 유의미할 것으로 예상
이항 로지트 모델
Pr (심사 더미 = 1) = F ( a + b1 연봉 + b2 여성 더미 + b3 결혼 더미 )

(2) 투자펀드 대상기업에 대한 답변
서(2006)는 무라카미 펀드와 스털링 파트너스라는 투자 펀드가 어떤 기업을 대상으로 투자를 하는지를 분석하였다.
그 결과 기업가치가 낮고, 현금과 예금이 많으며, 부채비율이 낮고, 주식보유비율이 낮은 기업을 대상으로 하고 있음을 알 수 있다.
또한 이노우에와 가토(2007)도 마찬가지로 6개 투자펀드의 투자행태를 분석하였다.
거기서 주가가 저평가되어 있고 실적이 좋지 않은 기업이 타깃이 되고 있다는 것을 알 수 있습니다.
이러한 선행연구를 최대한 재현하고자 합니다.
어떤 데이터(어떤 기업의 데이터가 대상인가? 어떤 데이터를 얻을 수 있을 것인가?) 를 이용하여 어떤 분석(회귀분석식, 각 설명변수의 계수 부호 예측)을 하면 좋을까요?
실제 데이터를 취득하여 분석하는 것은 요구하지 않습니다.
설명변수: 투자펀드의 투자를 받은 경우 = 1, 받지 않은 경우 = 0 → '투자펀드 더미'
데이터 대상 : 전체 상장기업
투자를 받았는지 안 받았는지 여부가 포함되어 있는가?
예: SPEEDA, MARR M&A 데이터 CD-ROM, 레코프 M&A 데이터베이스, 닛케이 기업활동 정보, 닛케이 텔레콘 21
Nikkei NEEDS-FinancialQUEST, eol, Yahoo!Finance, 회사 사계절 보고서, Nikkei Value Search

서(2006)는 무라카미 펀드와 스테이 기업가치가 낮고, 현금과 예금이 많으며, 부채비율이 낮고, 주주총회 보유비율이 낮은 기업이 표적이 되고 있음을 밝혔다.
주가가 저평가되어 있고 실적이 좋지 않은 기업이 타깃이 되는 것으로 알려져 있다.
Pr (투자펀드 더미 = 1) = F ( a + b1 시가총액비율 + b2 현금예금비율 + b3 부채비율 + b4 자기자본비율 + b5 ROA )
기업가치가 낮다 → b1 시가장부가액비율 마이너스
현금과 예금이 많음 → b2 현금예금비율 플러스
부채비율이 낮다 → b3 부채비율 마이너스
주주총회 지분율이 낮은 기업 → b4 지분율 마이너스
실적이 좋지 않은 기업 → b5 ROA 마이너스

연습5 사장 교체의 결정 요인
실적이 악화된 기업에서 경영자가 교체되는 것은 당연해 보인다.
과연 이런 일이 일어나고 있는 것일까?
그래서 경영자 교체의 결정요인을 분석해 보기로 한다.
여기서의 데이터는 1992년부터 2008년까지 일본 상장기업 552개사의 데이터이다.
이 기간 동안 약 300번의 사장 교체가 이루어졌다.
재무 데이터는 일본정책투자은행・일본경제연구소『기업재무데이터뱅크』에서 가져왔습니다.
- 설명변수 : ROA, 외국인 지분율, 자산(대수), 외국인 지분율과 ROA의 교차항
- 모두 1년 전 값.
실적이 악화되면 그 해가 아닌 다음 해에 사장이 교체되는 것이 아닌가 하는 생각에서 비롯된 것이다. → '1기 시차' - 회귀분석: LPM과 로지트 모델

(1) ROA와 사장교체와의 관계에서 어떤 것을 읽어낼 수 있는지 간단히 설명하시오.
(2) 외국인 지분율과 ROA의 교차항에 대해 어떤 것을 읽어낼 수 있는지 설명하시오.
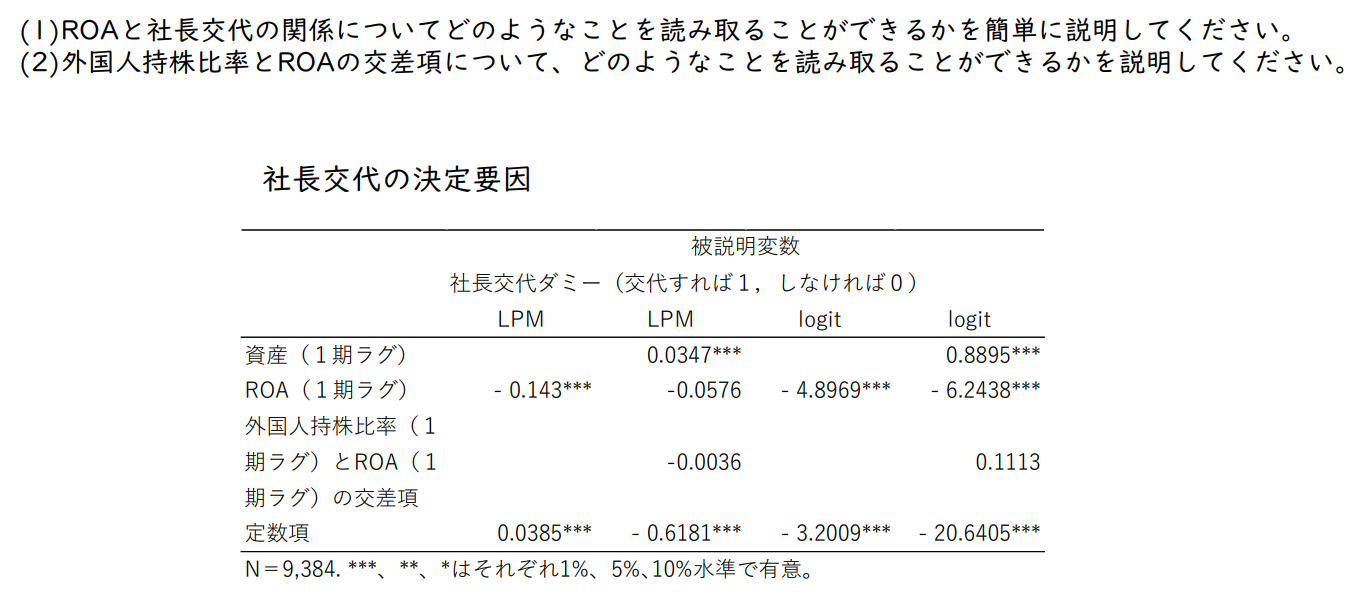
연습5 사장 교체의 결정 요인
(1) ROA와 사장교체와의 관계에서 어떤 것을 읽어낼 수 있는지 간단히 설명하시오.
(2) 외국인 지분율과 ROA의 교차항에 대해 어떤 것을 읽어낼 수 있는지 설명하시오.
설명변수: 사장 교체 더미
교체 = 1, 교체하지 않음 = 0
Pr ( Y = 1\X) = F ( a + b1 X )
X라는 정보(여기서는 ROA)가 주어졌을 때 Y=1을 취할 확률을 나타낸다.
- ROA가 마이너스이고 유의적 실적 악화 이듬해에 사장 교체
- 교차항(외국인 지분율과 ROA)의 계수가 마이너스로 유의하다면 '외국인 지분율이 높은 기업에서 ROA와 사장교체의 관계가 강하다'고 할 수 있지만, LPM과 Logit 모두 유의하지 않다.


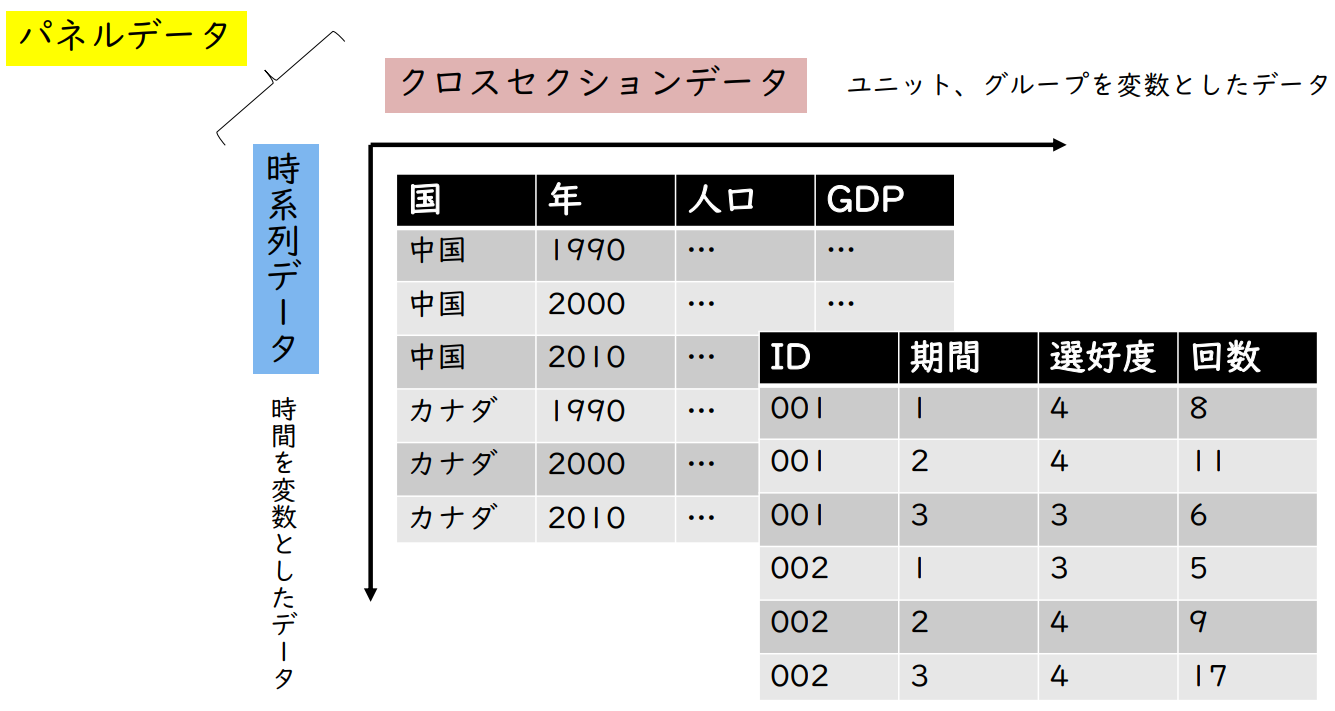
패널 데이터 분석

| 패널 데이터 | Cross-Sectional Data → | 단위, 그룹을 변수로 한 데이터 |
| 시계열 데이터 ↓ | 시간을 변수로 한 데이터 |
Financial_analysis 데이터
외국인 지분율과 ROA에 미치는 영향 분석
→외국인 지분율이 높은 기업일수록 ROA가 높다.
1,874개의 데이터를 횡단면, 시계열 데이터를 혼합하여 수집.
개별 기업 특성이나 시간의 변화를 고려하지 않고 회귀분석.
→ 풀링(Pooling) 회귀모델
시간 변화의 영향이 없고, 개별(이 경우 기업) 차이가 보이지 않을 때 효과적

패널 데이터의 사용 목적
예시
취업률이 결혼 여부와 미혼 여부에 영향을 미치고 있다.
결혼 더미 = α + β1 * 취업률 + μ
종교나 국가의 사고방식(예: 빨리 취업하는 것을 좋게 여기는 관습)이 취업률에 영향을 미치고 있다고 생각하지만, 관찰할 수 없다.
이대로 분석하면 설명변수 X와 상관관계가 있어 정확한 분석 결과를 얻을 수 없다.
그래서 패널 데이터를 사용하여 분석의 정확도를 높인다.

패널 데이터 분석 예시
구체적 사례
적성검사를 통해 우수한 학생을 채용하고자 하는 기업의 채용정책이 입사 후 성과에 효과가 있는지,
효과가 있다면 어느 정도인지 파악하는 것
데이터
2개 변수
➢ 5년 후의 성과
➢ 입사 시 적성검사 값: 분석의 관심 대상인 설명 변수

5년 후의 성과에 영향을 미칠 수 있는 요인을 가능한 한 많이 모형에 넣는다.
다른 요인들, 예를 들어 '경영이념이 기업에 얼마나 침투해 있는지'가 영향을 미칠 수 있지만,
측정이 어려워 데이터를 수집하기 어려울 수도 있다.
그래서,
➢ 만약 그러한 요인이 기업마다 시간을 통해 일정하게 지속된다면....
➢ 패널 데이터가 있다면...
그러한 요인의 영향을 통제할 수 있다.
관측 불가능한 요인이 모델에서 빠져나가면서 누락변수 편향*이 발생하는 문제를 해결.
*모델이 실제 값에서 벗어나게 된다.
'고정효과'를 사용하여 추정

입사 시 적성검사 수치와 5년 후의 성과
➢ 유명 기업은 우수한 학생들만 채용하는가?
➢ 우수한 육성 교육 등을 제공하기 때문에 직원들의 성과가 높은가?
두 변수 간의 관계를 측정하는 회귀식
Yi = a + b Xi + ui

입사 시 평균 적성검사의 변화가 5년 후의 성과에 미치는 영향
- 입사 시 평균 적성검사 결과의 변화
- 5년 후의 평균 성과 변화
케이스1
입사 시 적성검사 수치가 상승한 기업에서 그 해에 입사한 직원의 5년 후 성과가 향상되었다면,
입사 시 적성검사 수치가 5년 후의 성과에 영향을 미쳤기 때문이라고 볼 수 있다.
→ 기업은 우수한 학생을 채용하면 된다.
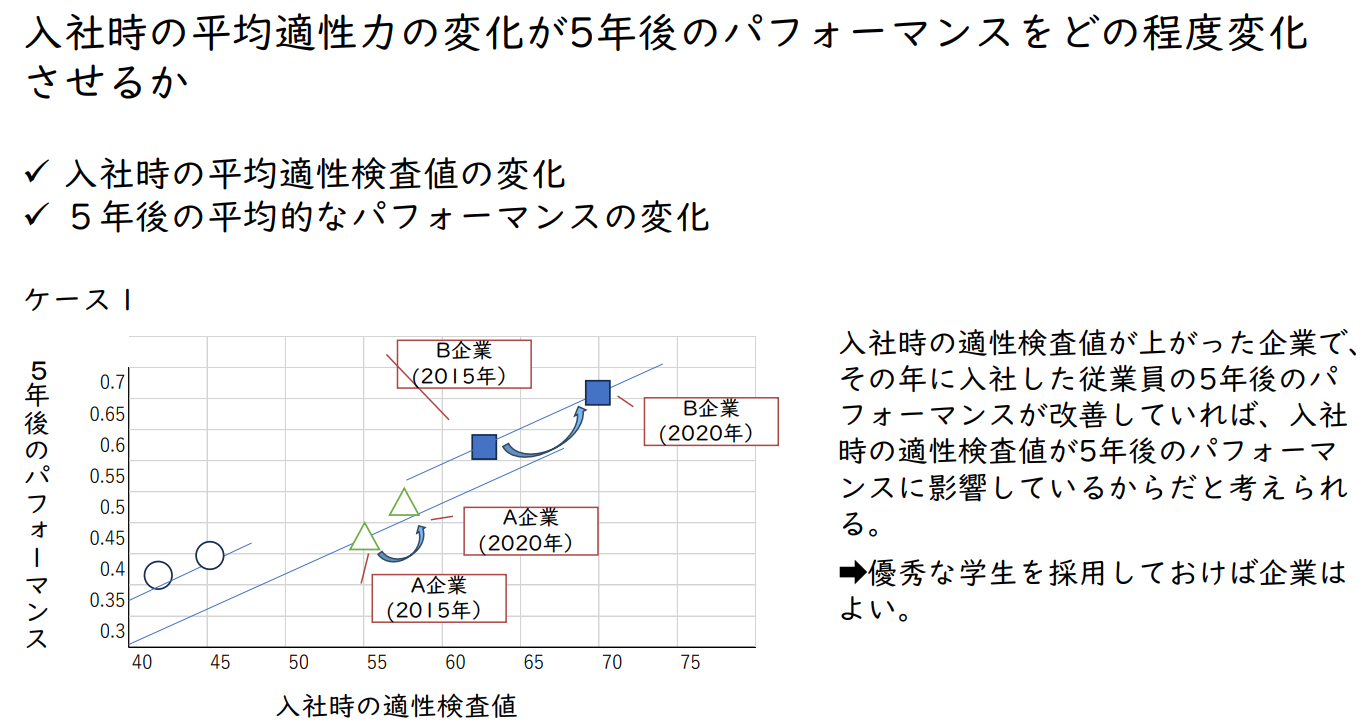
케이스2
입사 시 적성검사 값의 변동에 관계없이 직원의 5년 후 성과가 변하지 않는다면,
입사 시 적성검사 값은 5년 후 성과에 영향을 미치지 않는 것으로 간주되며,
→ 5년 후 성과는 각 기업의 특색에 따라 결정된다.
즉 기업의 육성의 질이 중요하다고 볼 수 있다.

고정효과 모델
Case 1, 2 모두 기업 𝑖의 절편은 다르지만 기울기는 같음
→ 각 기업 직원 5년 후의 성과 𝑌𝑖는 입사 시 적응력 𝑋𝑖와 각 기업의 특성 𝛼𝑖에 의해 결정된다고 본다.
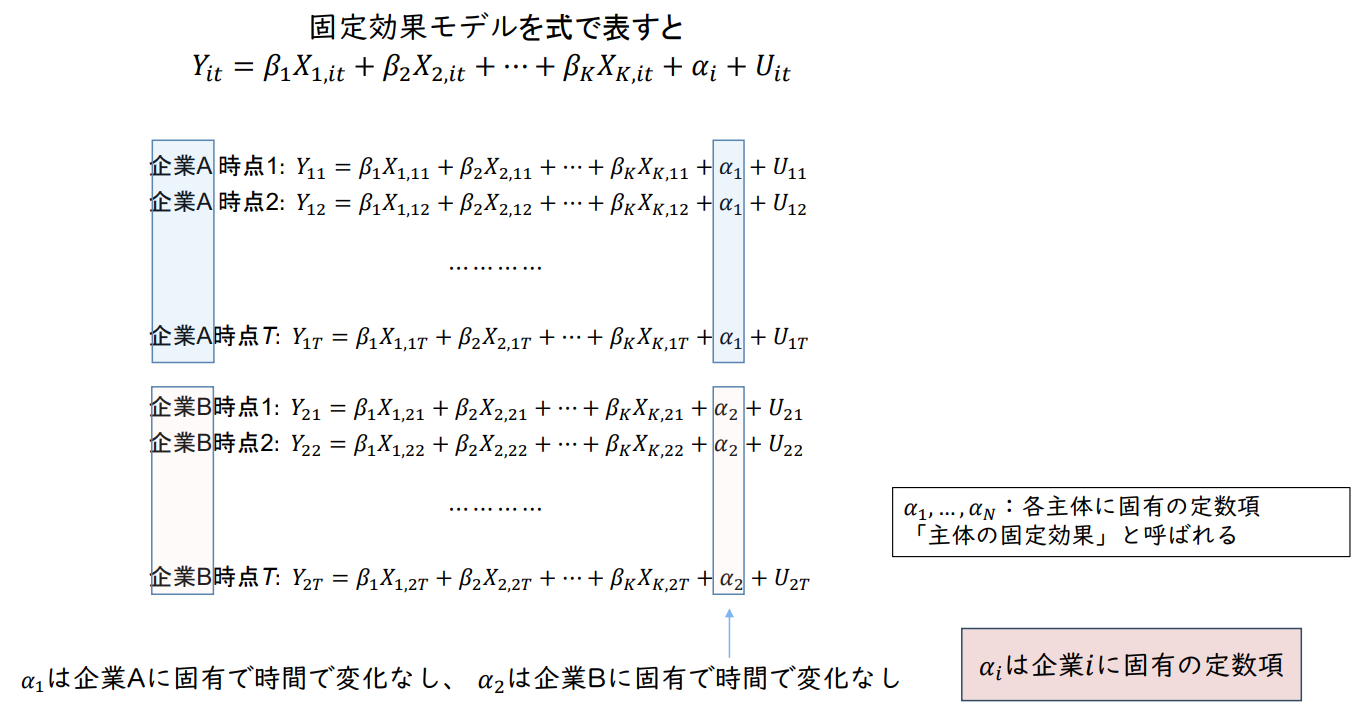
𝑌ᵢₜ = 𝛽₁ 𝑋₁,ᵢₜ + 𝛽₂ 𝑋₂,ᵢₜ + ⋯ + 𝛽ₖ𝑋ₖ,ᵢₜ + 𝛼𝑖 + 𝑈ᵢₜ
𝑌𝑖𝑡: 주체 𝑖의 시점 𝑡에서 종속변수의 값 (예: 5년 후의 성과)
𝑋𝑖𝑡: 주체 𝑖의 시점 𝑡에서의 설명변수 값 (예: 입사 시 적성검사 값)
𝛼𝑖 : 개별 기업의 특성
𝑖 = 1, ... , 𝑁; 𝑡 = 1, ... , T

회귀 직선의 기울기 계수는 기업마다 동일합니다.
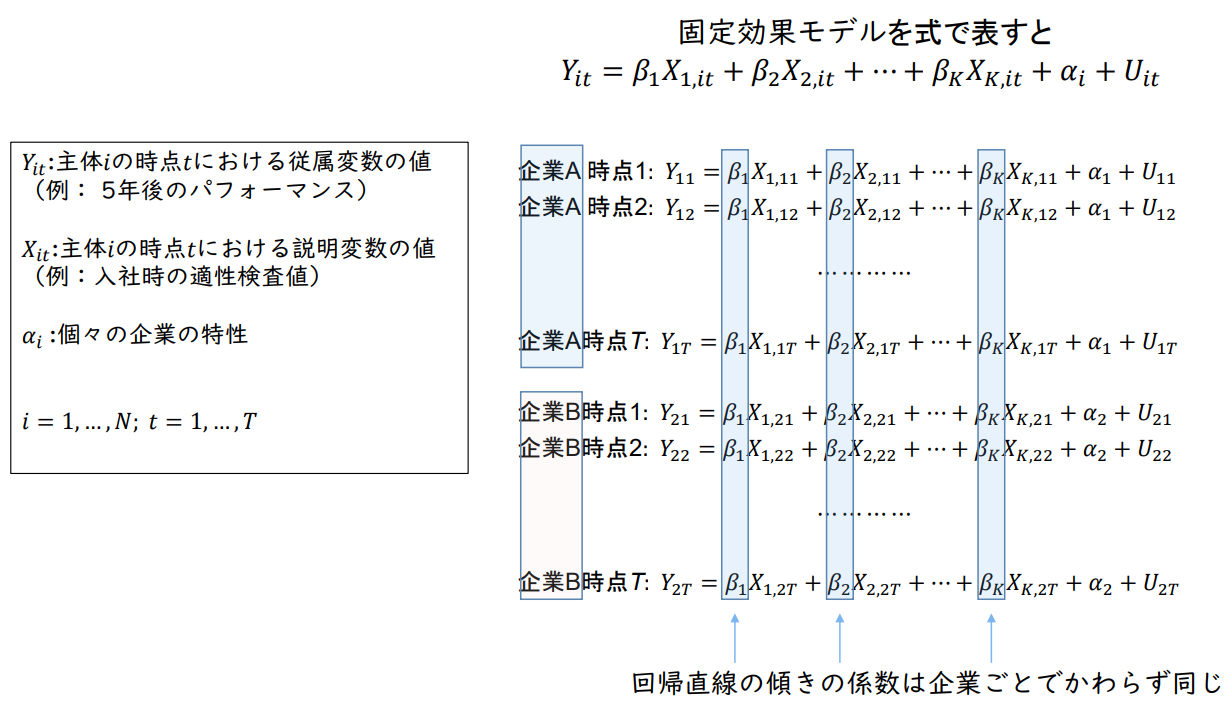
𝛼1, ... , 𝛼𝑁: 각 주체별 고유 상수항
'주체 고정효과'라고 불림
𝛼𝑖는 기업 𝑖에 고유한 상수항
𝛼1은 기업 A에 고유하며 시간에 따른 변화 없음, 𝛼2는 기업 B에 고유하며 시간에 따른 변화 없음
'주체의 고정효과' 정리
𝑌ᵢₜ = 𝛽₁ 𝑋₁,ᵢₜ + 𝛽₂ 𝑋₂,ᵢₜ + ⋯ + 𝛽ₖ𝑋ₖ,ᵢₜ + 𝛼𝑖 + 𝑈ᵢₜ
- 𝛼𝑖는 기업 𝑖 고유의 상수항
➢ 각 기업의 특성이기 때문에 기업마다 다르다.
➢ 상수항인 이유는 시간이 지나도 변하지 않기 때문이다. - 𝛼𝑖는 기업의 특성을 요인으로 하는 '효과'로 해석할 수 있기 때문이다,
𝛼1, ..., 𝛼𝑁는 '기업 고정효과'라고 한다.
➢ 𝑖가 개인을 나타낸다면, 𝛼1, ..., 𝛼𝑁는 '개인 고정효과'이다.

더미변수를 사용해도 기업의 고정효과를 나타낼 수 있습니다.
기업별로 더미변수를 생성하여 설명변수에 추가
𝑌ᵢₜ = 𝛽₁ 𝑋₁,ᵢₜ + 𝛽₂ 𝑋₂,ᵢₜ + ⋯ + 𝛽ₖ𝑋ₖ,ᵢₜ + 𝑑₂ 𝐷₂ᵢ + 𝑑₃𝐷₃ᵢ + ⋯ + 𝑑ₙ𝐷𝑁ᵢ + 𝑈ᵢₜ
기본 카테고리는 기업1 → 삭제
𝐷1𝑖를 모델에 넣으면 완전한 다중 공선성

입사 시 적성검사 결과와 5년 후의 성과
- 모두 계수가 양(+)으로 유의미함
- 풀링 모델보다 고정효과 모델에서 수치가 더 작게 나타남.
→ 입사 시 적성검사 값의 영향이 제한적

시간의 고정효과
각 주체별로 차이는 없지만 시간이 지남에 따라 변화하는 요인
예시
주세가 교통사고 사망률에 영향을 미치고 있다고 가정한다.
예를 들어, 주류의 정의는 시간이 지남에 따라 변화하지만, 같은 해에 각 도도부현 간에 차이가 없다.
이 주류의 정의는 주세 및 교통사고 사망률에 영향을 미칠 수 있다.
→ 주체 간 차이가 없지만, 시간이 지남에 따라 변하는 변수로 인한 누락 변수의 영향을 제거할 수 있다.

𝑌𝑖𝑡 = 𝛽₀ + 𝛽₁𝑋𝑖𝑡 + 𝛽₂𝑆𝑡 + 𝑈𝑖𝑡
𝑆𝑡는 알코올성 음료의 정의를 나타낸다.
𝑆𝑡에 첨자 𝑖가 붙지 않은 것은 시간이 지남에 따라 변화하지만, 도도부현 간에는 동일하기 때문이다.
𝜆𝑡 = 𝛽₀ + 𝛽₂𝑆𝑡로 대체
𝑌𝑖𝑡 = 𝛽₁𝑋𝑖𝑡 + 𝜆𝑡 + 𝑈𝑖𝑡
이 모델은 각 시점마다 다른 상수항 𝜆𝑡를 가지며, 시점 𝑡의 '효과'로 해석.
→ 𝜆1,..., 𝜆𝑡는 '시간 고정효과'라고 한다.

주체와 시간의 고정효과 모델
𝑌𝑖𝑡 = 𝛽₀ + 𝛽₁𝑋𝑖𝑡 + 𝛽₂𝑆𝑡 + ... + 𝛽ₖ𝑋ₖ,ᵢₜ + 𝛼𝑖 + 𝜆𝑡 + 𝑈𝑖𝑡
𝛼1, ... , 𝛼𝑁는 '주체의 고정효과'
𝜆1, ... , 𝜆𝑇는 '시간 고정효과'
주체 및 시간 고정효과 모델
- 시간에 걸쳐 일정하지만 주체마다 다르며, 실제로는 관측값으로 관측되지 않는 설명요인
- 주체 간에는 동일하지만 시간에 따라 변화하는, 실제로는 관측값으로 관측되지 않는 설명요인

회귀분석 요약

단계
- 변수로 표현할 수 있는 가설 세우기 + 적절한 회귀 모델 선택
- 데이터 수집, 정리하기
- 산포도 그리기
- 다중회귀분석의 경우 설명변수 간 상관관계 분석하기
- 회귀분석 실시
- 결과 해석하기

회귀분석 모델
| 설명변수 X | → | 종속변수 Y |
| - 연속 변수 - 질적 값(더미 변수) |
- 연속 변수 - 질적 값(더미 변수) |
- 단순 선형 회귀 모델, 다중 회귀 모델
- 이항변수: 선형 확률 모형, 이항 로짓 모형, 이항 프로빗 모형
- 순서 척도 변수 : 순서 로짓 모델, 순서 프로빗 모델, 간격 회귀 모델
- 다항변수 : 다항 로지트 모델, 조건부 로지트 모델

결정계수 : 설명변수로 설명할 수 있는 비율(%)
0에서 1까지의 값을 취한다.
F검정에 따른 P값
회귀식의 모든 계수가 0일 가능성이 있는 확률
유의하면 '회귀식의 모든 계수가 0이 아니다'라고 말할 수 있다.
0.1=10%, 0.05=5%, 0.01=1% 수준
계수의 신뢰성
계수의 값이 0(=Y의 변동요인으로 작용하지 않을 확률)이 통계적으로 의미(유의성)가 있는지 여부.
0.1=10%, 0.05=5%, 0.01=1% 수준

t값이란?
회귀분석에서 얻어진 계수가 피설명변수의 변동요인이 되고 있는지 여부.
계수가 0인 경우, 분석 중인 변수들 사이에 관계가 없는 것을 의미한다.
이를 검증하기 위해 t값이라는 검정 통계량을 계산한다.
t = b / b분산
b의 분산이 작을수록 설명력이 높다 = t값이 클수록 좋다.
t값이 대체로 절대값으로 2 이상이면 '계수가 0이라는 가설'이 지지될 확률(p값)은 5% 이하이다.

어떤 설명변수가 피설명변수에 영향을 미치는가?
- 계수의 절대값의 크고 작음이 아니다.
- 표준편차 회귀계수
통계 소프트웨어에서 계수를 비교할 수 있도록 표준화한 값을 나타낸다.
표준편향회귀계수의 절대값 비교 - 엑셀의 t값으로 대략적인 경향을 파악한다.
t값의 절대값 비교

'WBS - 2023 Winter > 기업 데이터 분석' 카테고리의 다른 글
| (기업데이터 #11-12) 더미 변수, 교차항, 로지스틱 회귀 분석 (0) | 2024.01.20 |
|---|---|
| (기업데이터 #9-10) 다중회귀분석 (0) | 2024.01.13 |
| (데이터 #7-8) 연구 방법, 논문 작성 (0) | 2023.12.23 |
| (데이터 #5-6) 데이터 간의 관계 파악 | 상관관계, 인과관계, 단회귀 분석 (0) | 2023.12.16 |
| (데이터 #3-4) 일부 데이터로 전체 추정하기 | 정규분포, 표준정규분포, 확률, 추정과 t검정 (0) | 2023.12.09 |
| (데이터 #1-2) Introduction (0) | 2023.12.04 |



