기업 데이터 분석 가을학기
11, 12회 더미변수, 교차항, 로지스틱 회귀분석 2024년 1월 20일(토)
상학학술원 비즈니스금융연구센터 오노 카오리
Email: kaori.ono@aoni.waseda.jp

연습문제 3
회귀분석을 통해 가설을 검증해 봅시다.
가설
에너지 소비량은 그 나라의 부의 정도에 따라 결정되지 않을까?
데이터 정부 통계
- 국내총생산(GDP)
- 1인당 에너지 소비량
설명변수를 추가해 보자.

단계
- 데이터 수집, 정리
예: World Bank, EIA (Energy Information Administration), 환경부...등... - 산포도 그리기
- 다중회귀분석의 경우, 설명변수 간의 상관관계 분석을 한다.
- 회귀분석을 실시한다.
- 결과 해석




더미 변수

지금까지의 설명변수는 모두 수량
- 전용면적
- 건축연령
- 매출액
- ROA
- 근속연수...
⇒ 정량적 변수는 연속적 변수
얼마나 큰지 작은지를 나타낸다.
◆ 수치로 표현할 수 없는 '정성적' 요인을 회귀분석에 도입하여 영향력 검증도 가능

- 질적 변수의 예
- 남녀 등 성별
- 혈액형
- 일본인과 미국인
- 남향 또는 북향
- 거주 지역
- 기업이 속한 산업(건설업, 운수・통신, 상업, 금융・보험・부동산업...) ...
⇒ 이산적 변수
- 비슷한 설명변수라도 양적과 질적으로 나뉜다.
- 정량적 : 교육연수
- 질적 : 중졸, 고졸, 대졸, 대학원 졸업

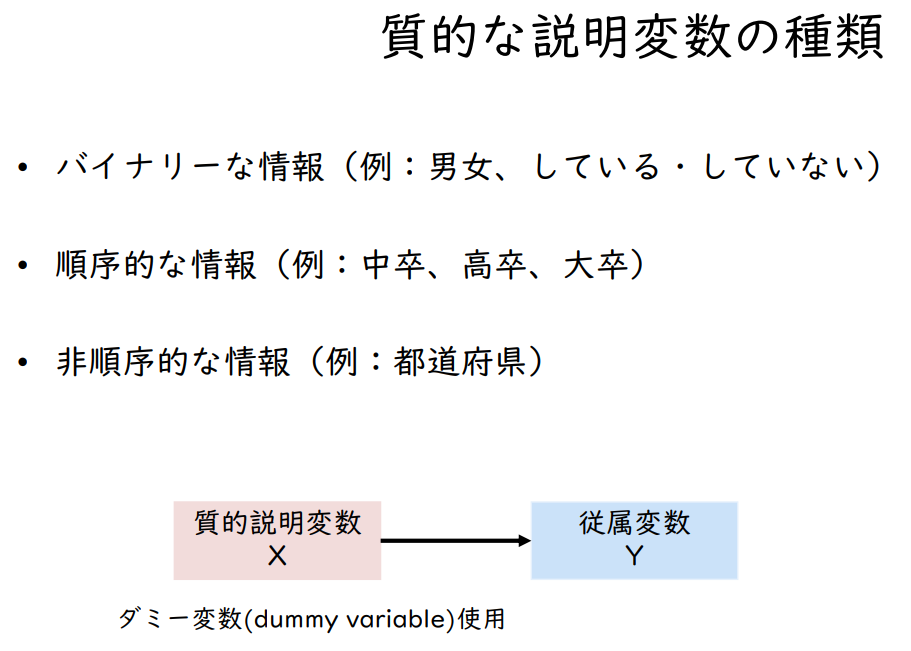
질적 설명변수의 종류
- 이분법적 정보(예: 남녀, 하고 있다/하지 않고 있다)
- 순차적 정보(예: 중졸, 고졸, 대졸)
- 비순차적 정보(예: 도도부현)
| 질적설명변수 X |
→ | 종속변수 Y |
더미변수(Dummy Variable) 사용
더미 변수가 바이너리
- 질적 요인을 분석하는 경우, 대부분 이항(0 또는 1)의 형태로 변수화
예시
- 남성/여성
- '있다/없다', '하고 있다/하지 않는다' → 0 or 1
- 스톡옵션을 도입하고 있다/하지 않고 있다
- 남성 직원에 대한 육아휴직 제도가 있다・없다
- 해외 진출 시 M&A를 하고 있다・하고 있지 않다
- 변수화
| 1. 남성 = 1, 여성 = 0 | ← | 어느 쪽이든 상관없다 둘 다 넣지 않음(다중공선성) 여성 + 남성 = 1 |
더미 변수를 입력하는 것을 '베이스 그룹'이라고 합니다. |
| 2. 여성 = 1, 남성 = 0 |

예: 성별이 임금에 영향을 미치는지 여부
𝑚𝑤𝑎𝑔𝑒 = 𝛽₀ + 𝛽₁𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
𝑚𝑤𝑎𝑔𝑒 : 월 급여
𝑓𝑒𝑚𝑎𝑙𝑒 : = 1 (여성) = 0 (남성)
𝑡𝑒𝑛𝑢𝑟𝑒 : 근속연수
𝑢 : 오차항
여기서 𝛽₁은 𝑓𝑒𝑚𝑎𝑙𝑒의 계수이다.
* 남성 = 1, 여성 = 0의 남성 더미로도 문제없다.

𝑚𝑤𝑎𝑔𝑒 = 𝛽₀ + 𝛽₁𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
𝑓𝑒𝑚𝑎𝑙𝑒 = 0 즉, 남자
𝑚𝑤𝑎𝑔𝑒 = 𝛽₀ + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒
𝑓𝑒𝑚𝑎𝑙𝑒 = 1
𝑚𝑤𝑎𝑔𝑒 = 𝛽₀ + 𝛽₁ + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒
𝛽1은 다른 요인을 통일했을 때 월 급여의 남녀 차이
→ 성차별이 있다

여성 = 1, 남성 = 0의 여성 더미
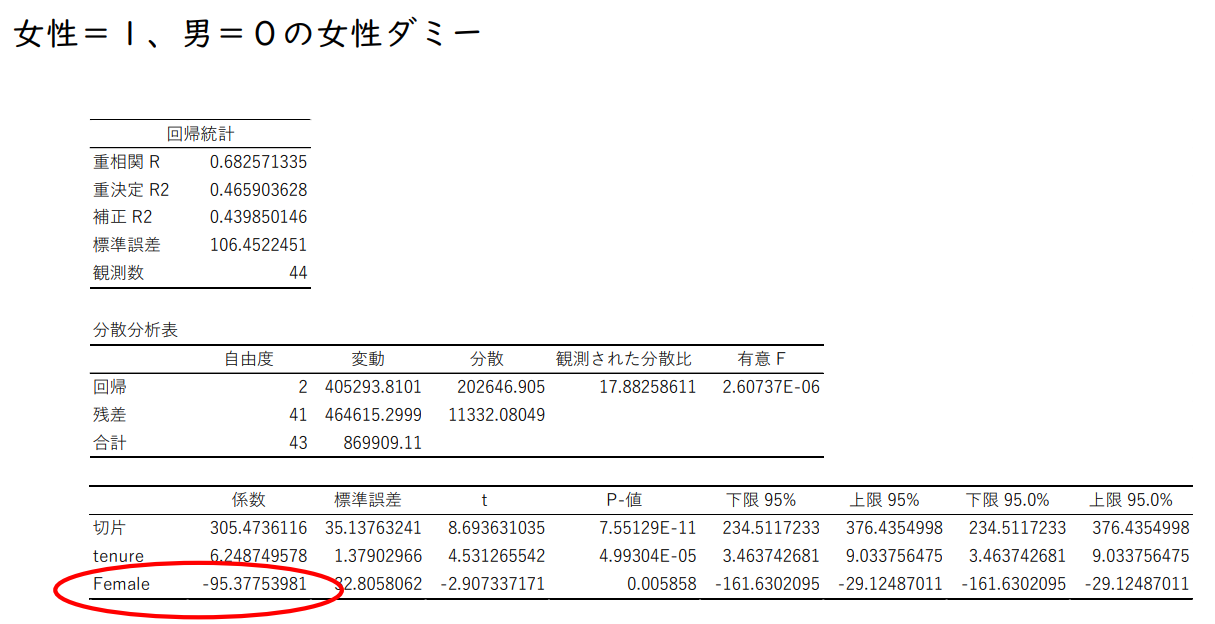
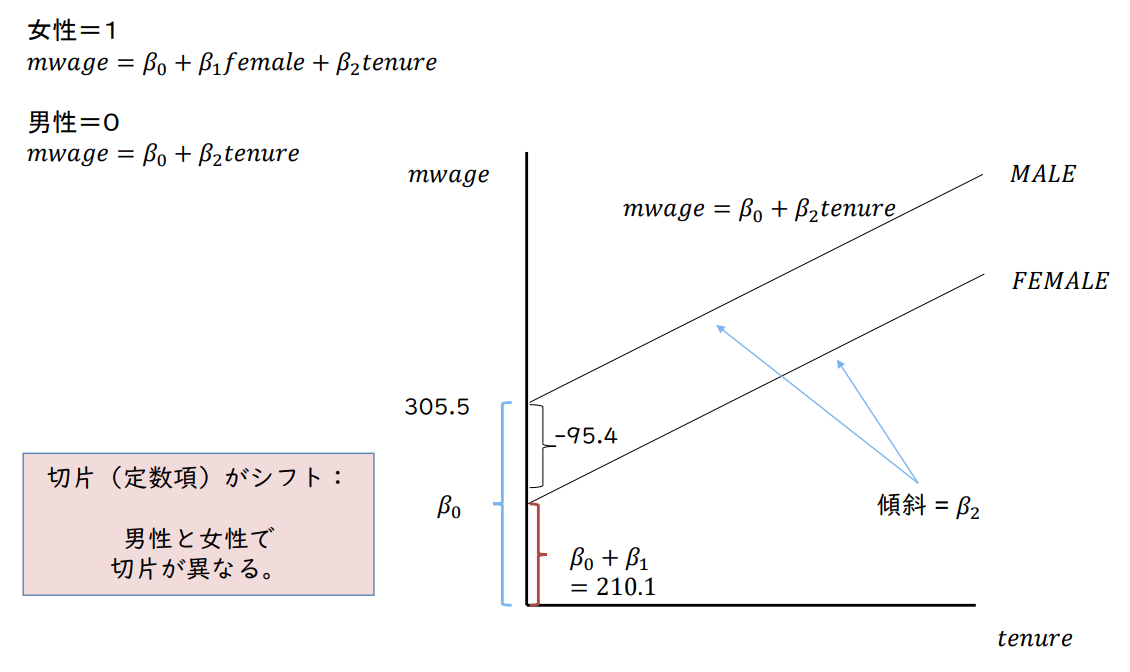
여성 = 1
𝑚𝑤𝑎𝑔𝑒 = 𝛽₀ + 𝛽₁𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒
남성 = 0
𝑚𝑤𝑎𝑔𝑒 = 𝛽₀ + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒
절편(상수항)이 이동: 남성과 여성에서 절편이 다르다.
더미 변수를 거꾸로 한 경우
𝑚𝑤𝑎𝑔𝑒 = 𝛼₀ + 𝛾₀𝑚𝑎𝑙𝑒 + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
여성 = 0
𝑚𝑤𝑎𝑔𝑒 = 𝛼₀ + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒
남성 = 1
𝑚𝑤𝑎𝑔𝑒 = 𝛼₀ + 𝛾₀ + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒
→ 여성 상수항 = 𝛼₀, 남성 상수항 = 𝛼₀ + 𝛾₀
표현은 다르지만 같은 것

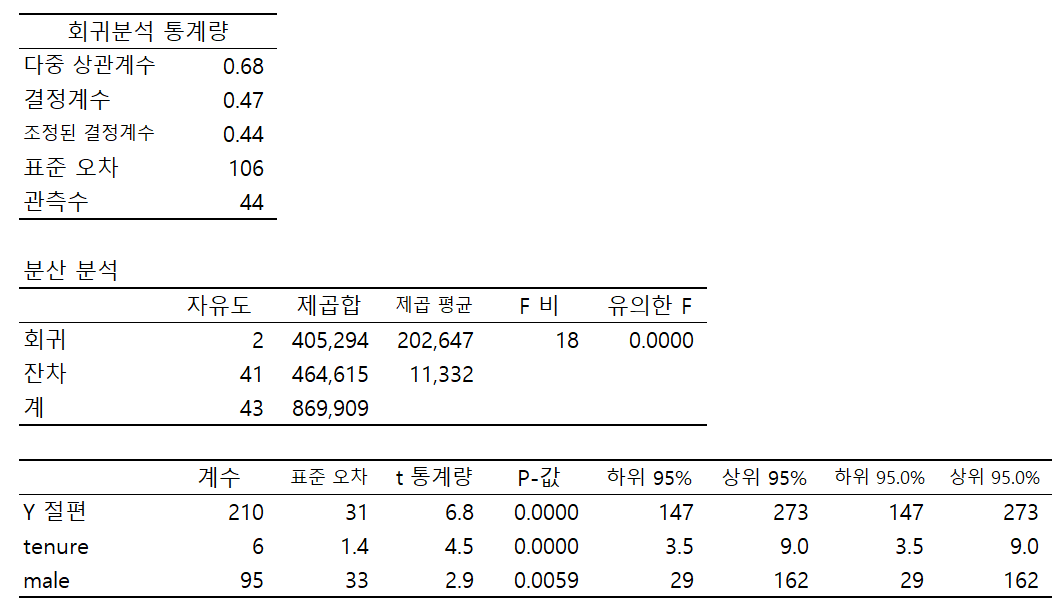
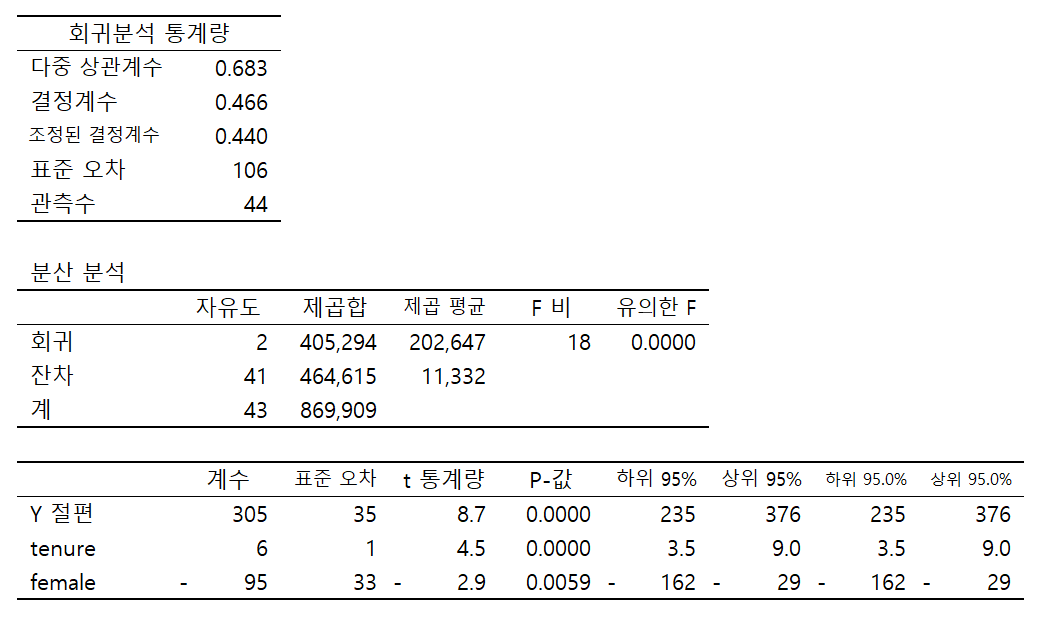
확인: 더미 변수
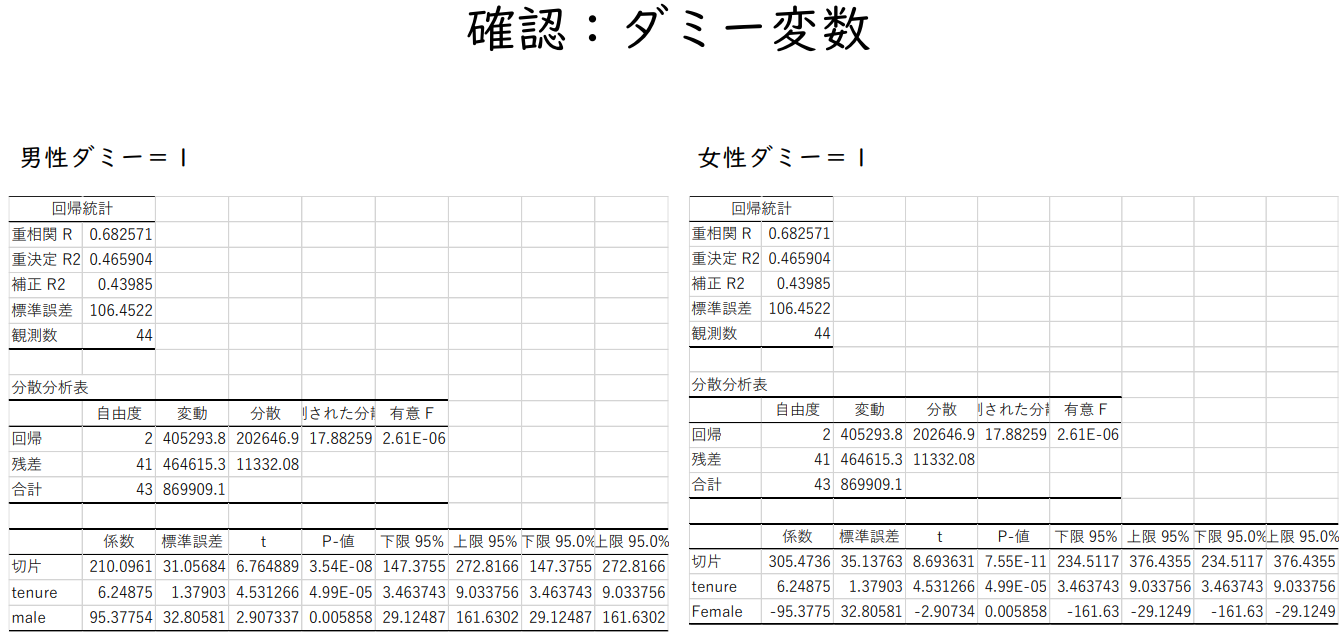
더미 변수가 여러 개
카테고리가 두 개 이상일 경우 더미 변수화
예: 교육수준
카테고리 : 고졸 미만, 고졸, 대졸 이상
| JH | 1 고졸미만 | HI | 1 고졸 | UN | 1 대졸이상 |
| 0 고졸, 대졸이상 | 0 고졸미만, 대졸이상 | 0 고졸미만, 고졸 |
- 반드시 더미변수 중 하나는 1의 값을 취하고, 다른 더미변수는 0의 값을 취한다.
→ 𝐽𝐻 + 𝐻 + 𝑈𝑁 = 1 이 성립한다.

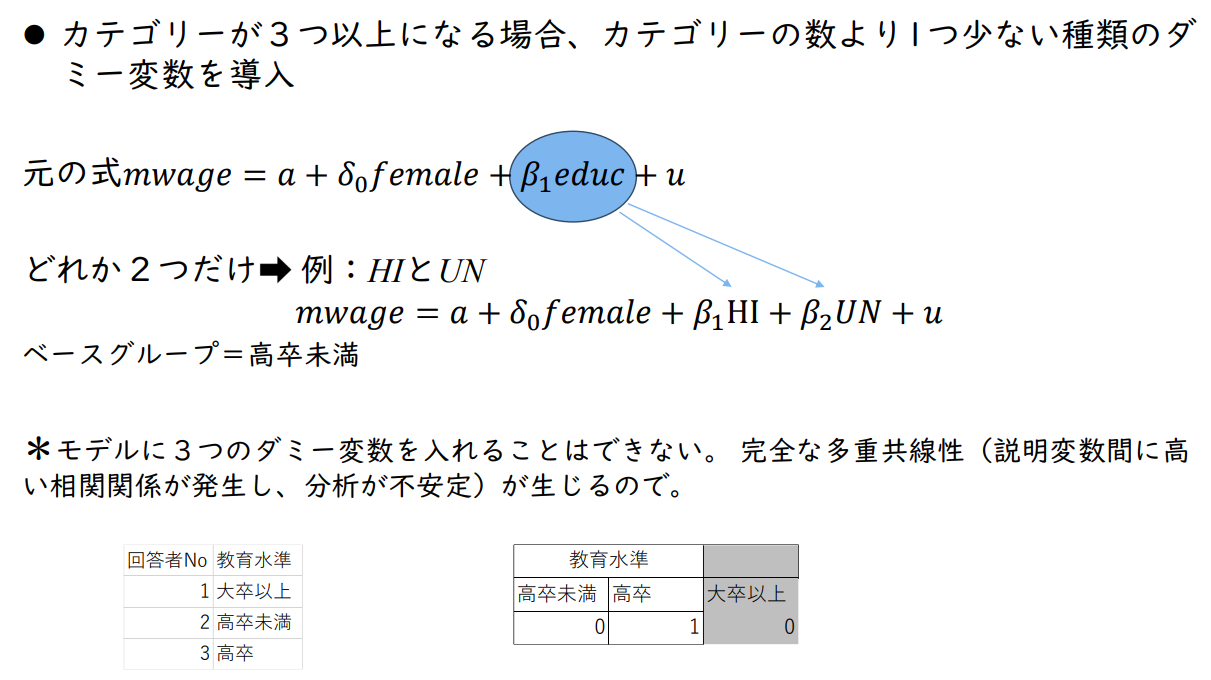
- 카테고리가 2개 이상일 경우, 카테고리 수보다 1개 적은 종류의 더미변수 도입
원래 식 𝑚𝑤𝑎𝑔𝑒 = 𝑎 + 𝛿₀𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₁𝑒𝑑𝑢𝑐 + 𝑢
어느 두 개만 : HI와 UN
𝑚𝑤𝑎𝑔𝑒 = 𝑎 + 𝛿₀𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₁HI + 𝛽₂𝑈𝑁 + 𝑢
기준그룹 = 고졸 미만
* 모형에 3개의 더미변수를 넣을 수 없음.
완전한 다중공선성(설명변수 간 높은 상관관계가 발생하여 분석이 불안정해짐)이 발생하기 때문이다.
| 회답자No | 교육수준 | 교육수준 | |||
| 1 | 대졸이상 | 고졸미만 | 고졸 | 대졸이상 | |
| 2 | 고졸미만 | 0 | 1 | 0 | |
| 3 | 고졸 |
𝑚𝑤𝑎𝑔𝑒 = 𝑎₀ + 𝛿₀𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽1HI + 𝛽2𝑈𝑁 + 𝑢
- 고졸 미만 : 𝑚𝑤𝑎𝑔𝑒 (𝑓𝑒𝑚𝑎𝑙𝑒, 𝐻I=0, 𝑈𝑁=0)= 𝑎₀ + 𝛿₀ 𝑓𝑒𝑚𝑎𝑙𝑒
- 고졸 : 𝑚𝑤𝑎𝑔𝑒 (𝑓𝑒𝑚𝑎𝑙𝑒, 𝐻I=1, 𝑈𝑁=0)= 𝑎₀ + 𝛽₁ + 𝛿₀ 𝑓𝑒𝑚𝑎𝑙𝑒
- 대졸 이상 : 𝑚𝑤𝑎𝑔𝑒 (𝑓𝑒𝑚𝑎𝑙𝑒, 𝐻I=0, 𝑈𝑁=1) = 𝑎₀ + 𝛽₂ + 𝛿₀ 𝑓𝑒𝑚𝑎𝑙𝑒
해석 방법
- 𝛽₁은 '고졸자의 월급이 기준 그룹인 고졸 미만자에 비해 평균적으로 얼마나 높은지(낮은지)'를 나타낸다.
- 𝛽₂는 '기준 그룹인 고졸 미만인 사람에 비해 대졸 이상 사람의 월급이 평균적으로 얼마나 높은지(낮은지)'를 묻는 것이다.
𝑚𝑤𝑎𝑔𝑒 = 238.2 - 67.7𝑓𝑒𝑚𝑎𝑙𝑒 + 0.03HI + 0.11𝑈𝑁

연습문제1 : 내점고객의 특성
- '고객특성.csv' 파일을 이용하여, 내점고객의 특성을 엑셀 등으로 분석해 보세요.
- 결과에 대해 해석을 추가해 보세요.
- 더미 변수로 변환 → IF 함수
* 일요일을 베이스 그룹으로 설정
* 모델에 모든 더미를 넣을 수 없음 → 삭제 - 회귀분석을 실행합

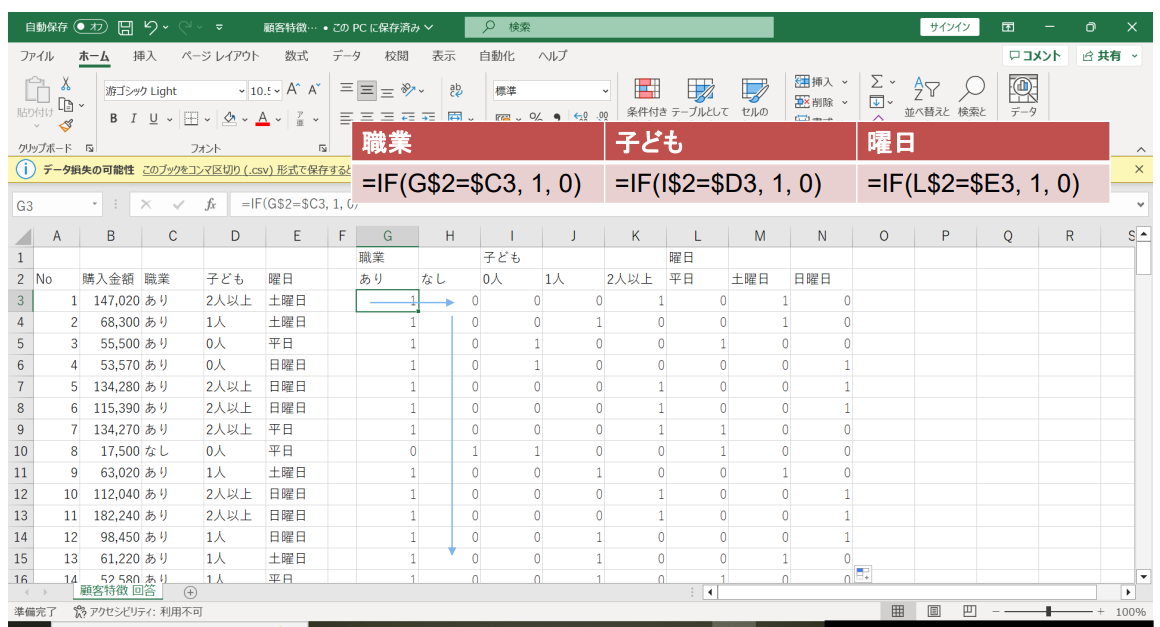
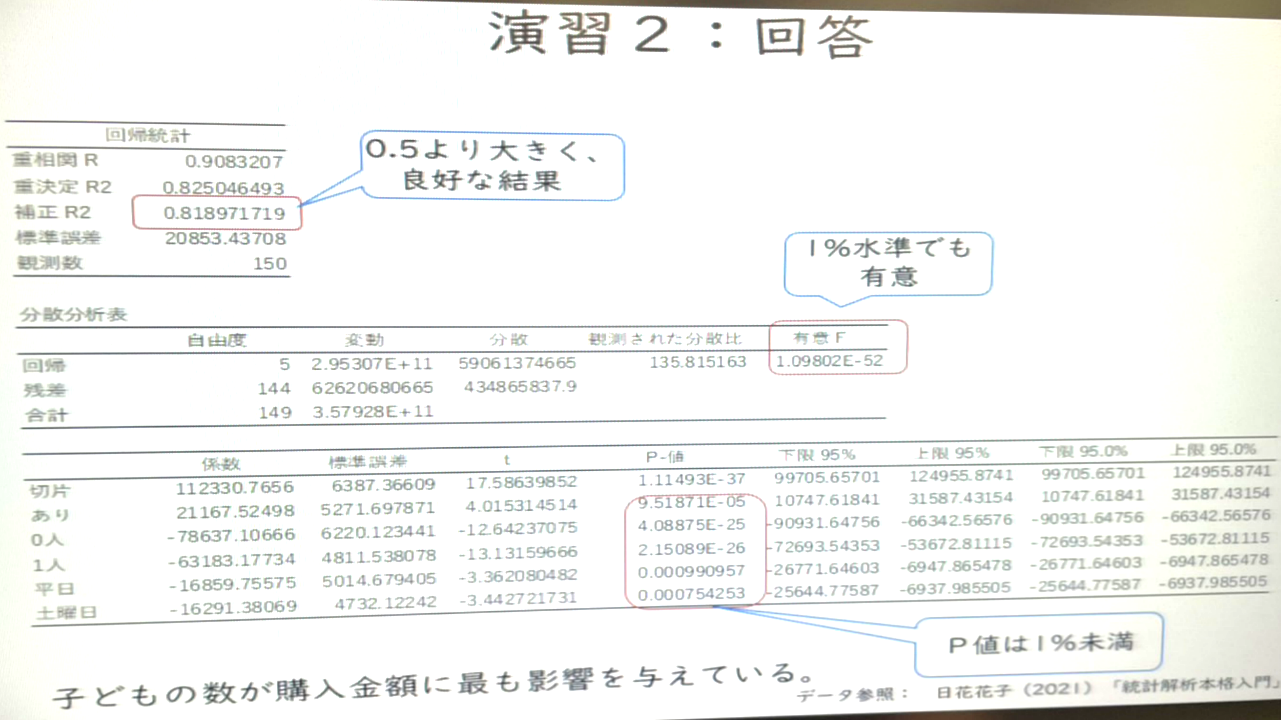
연습2 : 정답
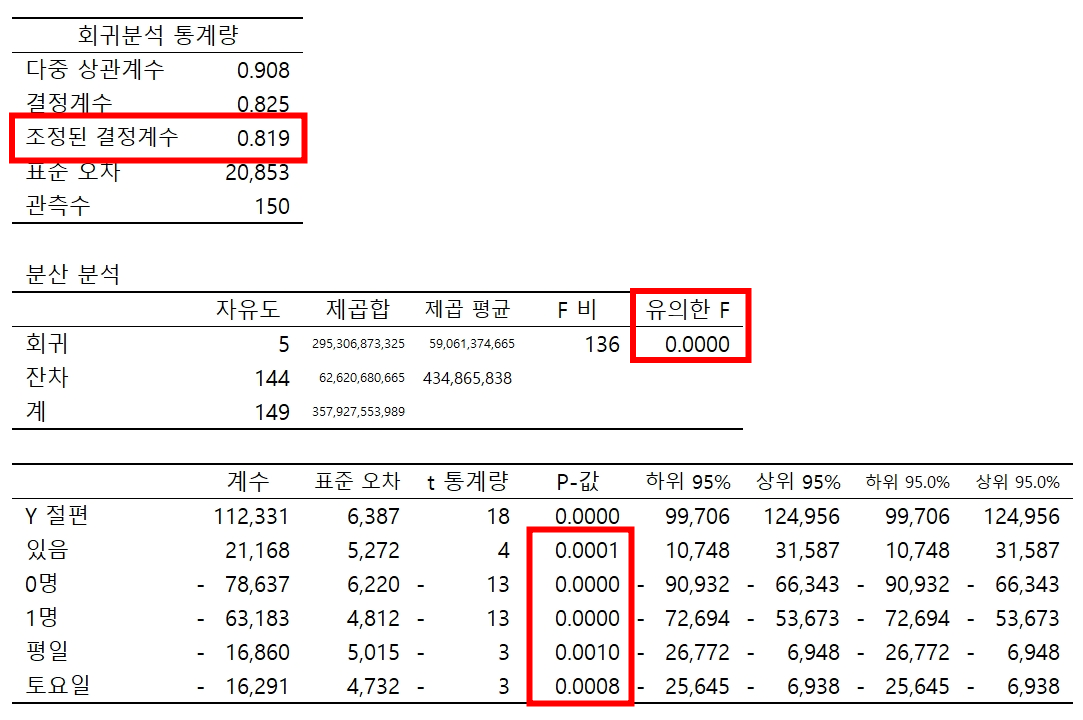
자녀의 수가 구매 금액에 가장 큰 영향을 미친다.
서수를 나타내는 더미 변수
서수란? 단순히 순서(서수)를 나타내는 것
예1
교육수준
고졸 미만(가장 작음), 고졸(두 번째로 큼), 대졸 이상(더 큼 = 세 번째)
예2
설문지에서 사람의 '신체적 매력'을 5단계로 평가해 주십시오. (1, 2, 3, 4, 5)

논문에 사용된 실제 데이터에 의한 더미 변수의 예시.
"육체적 매력이 노동시장에서 유리하게 작용하는지 여부."
- 조사자가 표본의 사람을 신체적 매력에 대해 5단계로 평가함.
평범함(1)
아주 평범하다(2)
평균(3)
잘생겼다(4)
눈에 띄게 아름답거나 잘생겼다(5) - 이 신체적 매력의 서수적 변수(𝐿𝑂𝑂𝐾𝑆) 외에 임금(𝑊𝐴𝐺𝐸), 교육수준(𝐸𝐷𝑈𝐶), 노동시장 경력(𝐸𝑋𝑃𝐸𝑅) 등의 변수가 데이터에 포함돼 있다.

더미 변수 설정 예시
| L1 | 1 평범 | L2 | 1 아주 평범 | L3 | 1 평균 | L4 | 1 잘생김 | L5 | 1 매우 매력 |
| 0 그외 | 0 그외 | 0 그외 | 0 그외 | 0 그외 |
ln 𝑊𝐴𝐺𝐸 = 𝛽₀ + 𝛽₁𝐿₂ + 𝛽₂𝐿₃ + 𝛽₃𝐿₄ + 𝛽₄𝐿₅ + ⋯

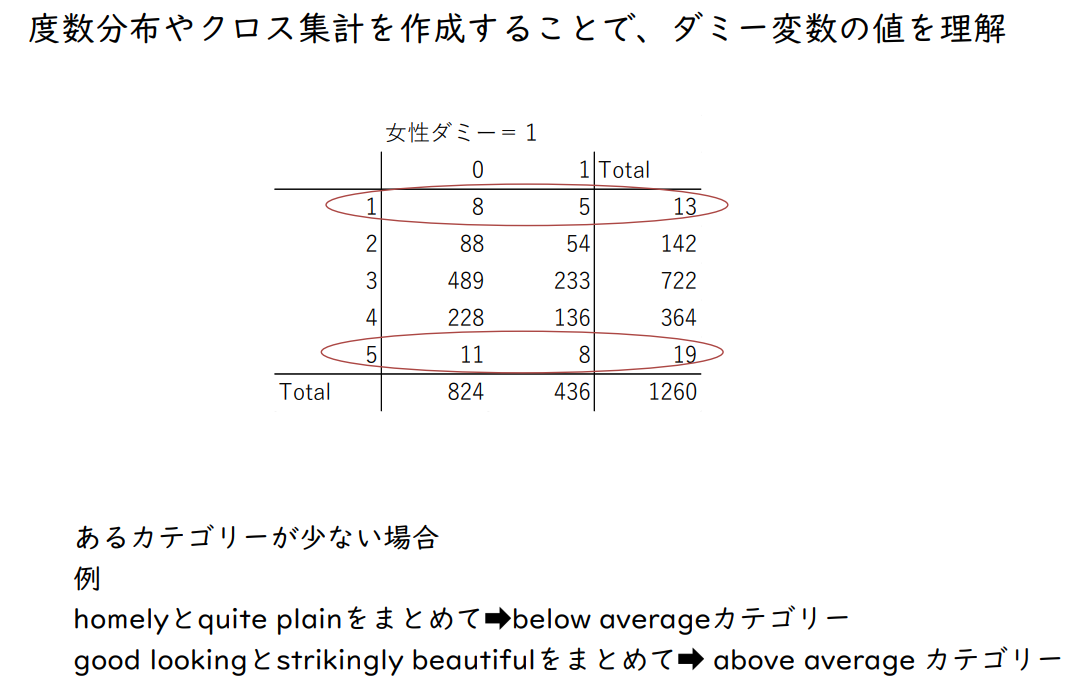
빈도 분포와 교차집계를 생성하여 더미 변수의 값을 이해합니다.
| 0 | 1 | Total | |
| 1 | 8 | 5 | 13 |
| 2 | 88 | 54 | 142 |
| 3 | 489 | 233 | 722 |
| 4 | 228 | 136 | 364 |
| 5 | 11 | 8 | 19 |
| Total | 824 | 436 | 1,260 |
특정 카테고리가 적은 경우
예시
homely와 quite plain을 묶어서 → below average 카테고리
good looking과 strikingly beautiful을 묶어서 → above average 카테고리
3개의 카테고리 중 𝐴𝑉𝐸𝑅𝐴𝐺𝐸를 베이스 카테고리로 설정
ln 𝑊𝐴𝐺𝐸 = 𝛽₀ + 𝛽₁𝐵𝐸𝐿𝐴𝑉𝐺 + 𝛽₂𝐴𝐵𝑉𝐴𝑉𝐺 + ⋯
- 𝛽₁의 해석은 "𝐴𝑉𝐸𝑅𝐴𝐺𝐸의 사람에 비해서, 𝐵𝐸𝐿𝑂𝑊 𝐴𝑉𝐸의 사람의 임금은..."
- 𝛽₂의 해석은 "𝐴𝑉𝐸𝑅𝐴𝐺𝐸의 사람에 비해서, 𝐴𝐵𝐵𝑂𝑂𝑉𝐸 𝐴𝑉𝐸의 사람의 임금은..."
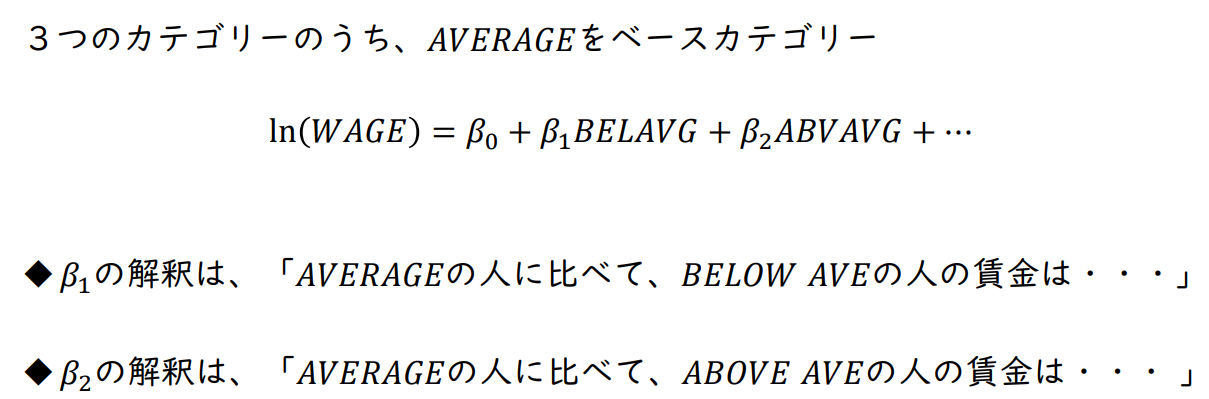
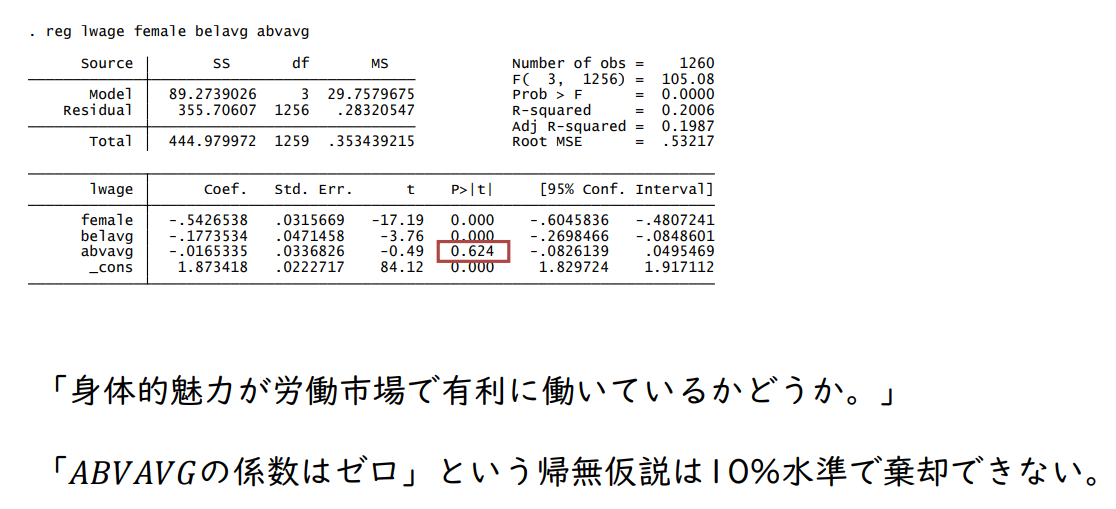
"신체적 매력이 노동시장에서 유리하게 작용하는지 여부."
'𝐴𝐵𝑉𝐴𝑉𝐺의 계수는 0이다'라는 귀무가설은 10% 수준에서 기각할 수 없다.
교차항

𝑚𝑤𝑎𝑔𝑒 = 𝛽₀ + 𝛽₁𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₂𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
이 공식이 의미하는 것은 남성이든 여성이든 근속연수가 월급에 미치는 영향은 𝛽₂로 일정하다는 것이다.
과연 그럴까?
근속연수에 따라 여성의 임금도 남성과 같은 상승폭을 유지할 수 있을까?
'근속연수가 급여에 미치는 효과는 성별에 따라 달라질 수 있다'는 가능성을 생각해 볼 수 있다.
이 공식은 이 가능성을 배제하고 있다.

| X₁ | → | Y |
| X₁ | → | Y |
| ↑ X₂ |
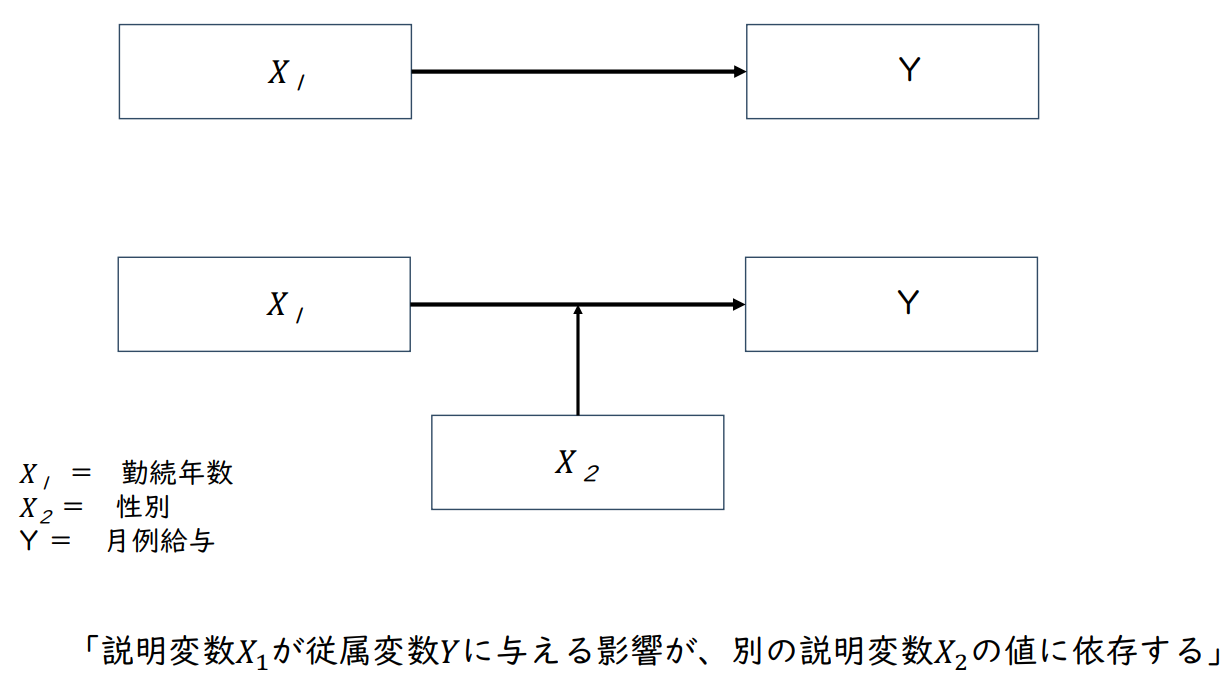
𝑋₁ = 근속연수
𝑋₂ = 성별
Y = 월별 수당
"설명변수 𝑋₁이 종속변수 Y 에 미치는 영향은 다른 설명변수 𝑋₂의 값에 따라 달라진다"
교차항(상호작용항)
설명변수 𝑋₁이 종속변수 𝑌에 미치는 영향에서 Z에 의존한다.
| 𝑋₁ 설명변수 | → | 𝑌 종속변수 |
| ↑ Z 조정변수 |
||
| 조정 변수(Moderator) 연속변수든 더미변수든 상관없습니다. 설명변수와 조정변수를 곱한 Z・𝑋₁ = 𝑋₂ 설명변수 |
||
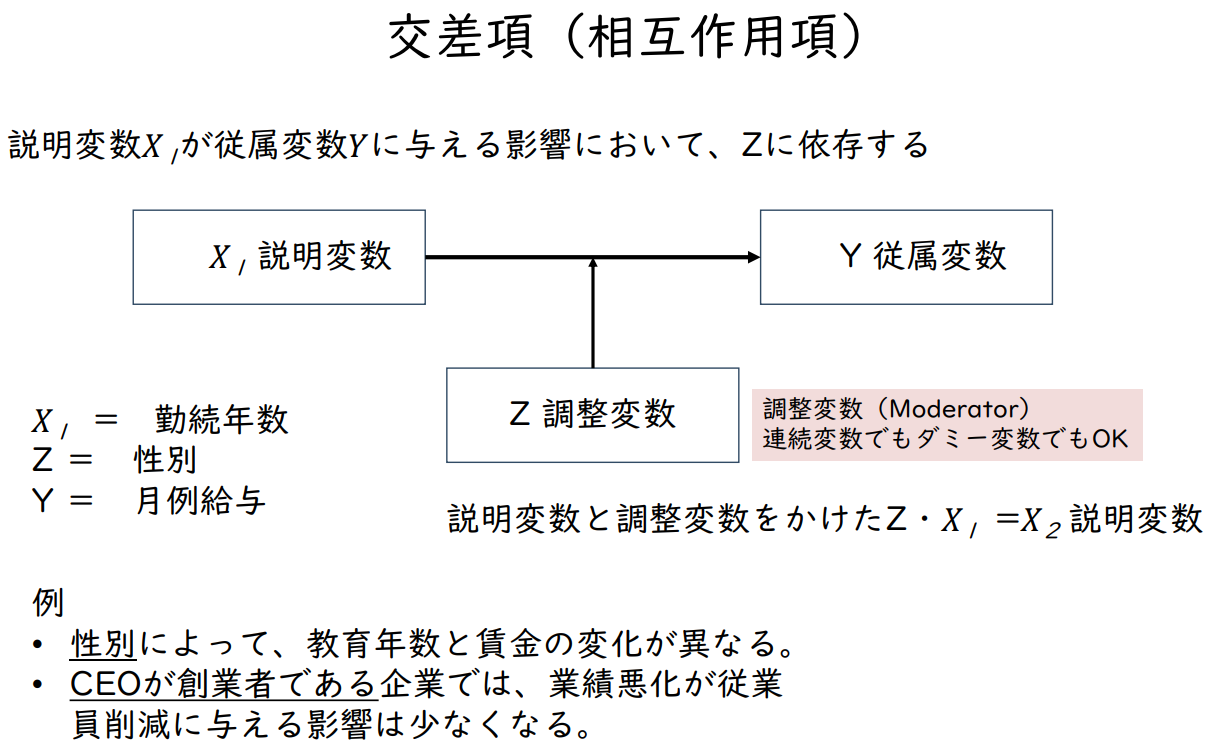
𝑋₁ = 근속연수
𝑋₂ = 성별
Y = 월별 수당
예시
- 성별에 따라 교육연수와 임금의 변화가 다르다.
- CEO가 창업자인 기업에서는 실적 악화가 직원 감축에 미치는 영향이 적다.
남성과 여성은 근속연수가 높아질수록 격차가 확대된다는 가설을 세웠을 경우
⇒ 교차항 (설명변수 x 설명변수 → 또 다른 변수 생성)
𝑚𝑤𝑎𝑔𝑒 = 𝑎₀ + 𝛽₁𝑡𝑒𝑛𝑢𝑟𝑒 + 𝛽₂𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₃ 𝑓𝑒𝑚𝑎𝑙𝑒 x 𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
"근속연수가 월급에 미치는 영향은 성별에 따라 달라질 수 있다." 가능성을 고려할 수 있다.

𝑚𝑤𝑎𝑔𝑒 = 𝑎₀ + 𝛽₁𝑡𝑒𝑛𝑢𝑟𝑒 + 𝛽₂𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₃𝑓𝑒𝑚𝑎𝑙𝑒 x 𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
더미변수 : 여성 = 1, 남성 = 0
남성: 𝑚𝑤𝑎𝑔𝑒 = 𝑎₀ + 𝛽₁𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
여성: 𝑚𝑤𝑎𝑔𝑒 = 𝑎₀ + 𝛽₁𝑡𝑒𝑛𝑢𝑟𝑒 + 𝛽₂ + 𝛽₃ 𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
= (𝑎₀ + 𝛽₂) + ( 𝛽₁ + 𝛽₃ ) 𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
𝑡𝑒𝑛𝑢𝑟𝑒가 월급에 미치는 영향은 남성은 𝛽₁, 여성은 𝛽₁ + 𝛽₃
교차항의 계수 𝛽₃은 근속년수 효과의 남녀 차이를 포착하는 계수

처음부터 남녀 격차가 있었고, 근속연수에 따라 그 차이가 커졌다.
𝑚𝑤𝑎𝑔𝑒 = 𝑎₀ + 𝛽₁𝑡𝑒𝑛𝑢𝑟𝑒 + 𝛽₂𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₃𝑓𝑒𝑚𝑎𝑙𝑒 x 𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
남성: 𝑚𝑤𝑎𝑔𝑒 = 𝑎₀ + 𝛽₁𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
여성: 𝑚𝑤𝑎𝑔𝑒 = 𝑎₀ + 𝛽₁𝑡𝑒𝑛𝑢𝑟𝑒 + 𝛽₂ + 𝛽₃𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢
= (𝑎₀ + 𝛽₂) + (𝛽₁ + 𝛽₃) 𝑡𝑒𝑛𝑢𝑟𝑒 + 𝑢

교차항의 종류
- X₁이 연속 변수, X₂가 더미 변수
예시 𝑋₁ = 근속연수, X₂ = 성별 - X₁이 더미 변수, X₂도 더미 변수
- X₁이 연속 변수, X₂도 연속 변수

② X1 이 더미변수이고, X2도 더미변수이다.
Y = 𝛽₀ + 𝛽₁𝑑𝑢𝑚𝑚𝑦₁1 + 𝛽₂𝑑𝑢𝑚𝑚𝑦2 + 𝛽₃(𝑑𝑢𝑚𝑚𝑦1 x 𝑑𝑢𝑚𝑚𝑦2) + 𝑢
예: 외모(𝑑𝑢𝑚𝑚𝑦2)가 임금(Y)에 미치는 영향은 성별(𝑑𝑢𝑚𝑚𝑦1)에 따라 달라진다.
Y = 𝛽₀ + 𝛽₁ 성별 + 𝛽₂ 외모 + 𝛽₃(성별 x 외모)
- 성별(𝑑𝑢𝑚𝑚𝑦1): 여성 더미 = 1, 남성 = 0
- 외모(𝑑𝑢𝑚𝑚𝑦2): 외모 평균 미만=1, 외모 평균 이상=0

Y = 𝛽₀ + 𝛽₁𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₂𝐵𝐸𝐿𝐴𝑉𝐺 + 𝛽₃(𝑓𝑒𝑚𝑎𝑙𝑒 x 𝐵𝐸𝐿𝐴𝑉𝐺) + 𝑢
남성
- 외모 평균 이상 : 𝑓𝑒𝑚𝑎𝑙𝑒 = 0, 𝐵𝐸𝐿𝐴𝑉𝐺 = 0 → 𝛽₀
- 외모 평균 미만: 𝑓𝑒𝑚𝑎𝑙𝑒 = 0, 𝐵𝐸𝐿𝐴𝑉𝐺 = 1 → 𝛽₀ + 𝛽₂
남성의 경우, 외모가 평균 이하일 경우 효과 = 𝛽₂

Y = 𝛽₀ + 𝛽₁𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₂𝐵𝐸𝐿𝐴𝑉𝐺 + 𝛽₃(𝑓𝑒𝑚𝑎𝑙𝑒 x 𝐵𝐸𝐿𝐴𝑉𝐺) + 𝑢
여성
- 외모 평균 이상 : 𝑓𝑒𝑚𝑎𝑙𝑒 = 1, 𝐵𝐸𝐿𝐴𝑉𝐺 = 0 → 𝛽₀ + 𝛽₁
- 외모 평균 미만: 𝑓𝑒𝑚𝑎𝑙𝑒 = 1, 𝐵𝐸𝐿𝐴𝑉𝐺 = 1 → 𝛽₀ + 𝛽₁ + 𝛽₂ + 𝛽₃
여성의 경우, 외모가 평균 이하인 효과 = 𝛽₂ + 𝛽₃

Y = 𝛽₀ + 𝛽₁𝑓𝑒𝑚𝑎𝑙𝑒 + 𝛽₂𝐵𝐸𝐿𝐴𝑉𝐺 + 𝛽₃(𝑓𝑒𝑚𝑎𝑙𝑒 x 𝐵𝐸𝐿𝐴𝑉𝐺) + 𝑢
남성
- 외모 평균 이상 : 𝑓𝑒𝑚𝑎𝑙𝑒 = 0, 𝐵𝐸𝐿𝐴𝑉𝐺 = 0 → 𝛽₀
- 외모 평균 미만: 𝑓𝑒𝑚𝑎𝑙𝑒 = 0, 𝐵𝐸𝐿𝐴𝑉𝐺 = 1 → 𝛽₀ + 𝛽₂
여성
- 외모 평균 이상 : 𝑓𝑒𝑚𝑎𝑙𝑒 = 1, 𝐵𝐸𝐿𝐴𝑉𝐺 = 0 → 𝛽₀ + 𝛽₁
- 외모 평균 미만: 𝑓𝑒𝑚𝑎𝑙𝑒 = 1, 𝐵𝐸𝐿𝐴𝑉𝐺 = 1 → 𝛽₀ + 𝛽₁ + 𝛽₂ + 𝛽₃
교차항의 계수 𝛽₃은 외모가 평균 이하인 경우의 효과에 대한 남녀 차이를 나타낸다.

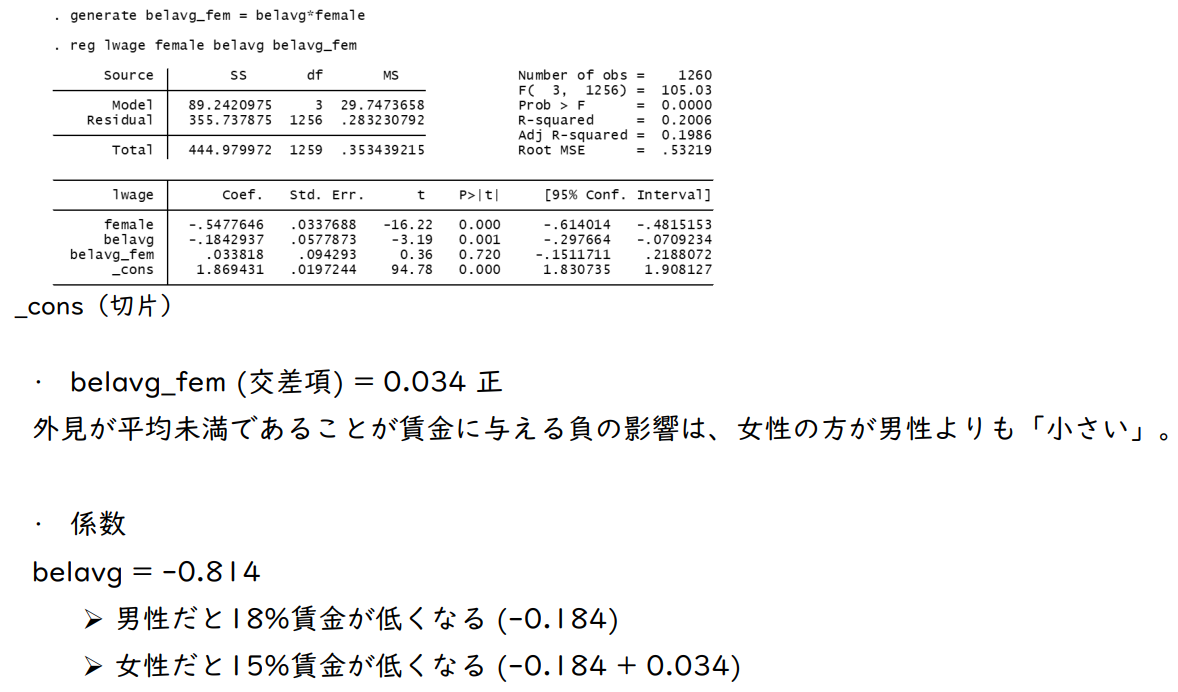
- belavg_fem (교차항) = 0.034 양(+)
평균 이하의 외모가 임금에 미치는 부정적 영향은 여성이 남성보다 '더 작다'. - 계수
belavg = -0.184
- 남성인 경우 18% 임금이 낮다 (-0.184)
- 여성인 경우 15% 낮은 임금 (-0.184 + 0.034)
- 교차항의 계수가 0이라는 귀무가설은 10% 유의수준에서 기각할 수 없다.
→ '외모가 평균 이하인 것이 임금에 미치는 영향은 성별에 따라 다르다'는 가설에 대한 충분한 통계적 지지를 얻지 못했다.

③ X1이 연속변수, X2도 연속변수
Y = 𝑎₀ + 𝛽₁𝑋₁ + 𝛽₂𝑋₂ + 𝛽₃(𝑋₁ × 𝑋₂) + 𝑢
예: 근속연수가 월급에 미치는 영향은 교육연수의 값에 따라 달라진다.
Y = 𝑎₀ + 𝛽₁ 교육연수 + 𝛽₂ 근속연수 + 𝛽₃(교육연수 × 근속연수) + 𝑢
- 교차항에 걸리는 계수 𝛽₃은 𝑋₁(교육연수)과 𝑋₂(근속연수)가 함께 변화할 때의 영향에 해당한다.
- 교육연수가 1.5배 변화하고, 근속연수가 1.5배 변화했을 때, 월급은 아래와 같이 예측할 수 있다.
(𝛽₁+𝛽₃ 근속연수) + (𝛽₂+𝛽₃ 교육연수) +𝛽₃

Y = 𝑎₀ + 𝛽₁ 교육연수 + 𝛽₂ 근속연수 + 𝛽₃(교육연수 × 근속연수) + 𝑢
- 근속연수의 연차 변화가 월급에 미치는 영향 𝛽₂ + 𝛽₃ 교육연수
만약 𝛽₃ >0이라면, 교육받은 연수가 많을수록 근속연수가 임금에 미치는 영향은 커진다. - 교육연수의 연차가 월급에 미치는 영향 𝛽₁ + 𝛽₃ 근속연수
교차항의 계수 𝛽3은 교육연수와 근속연수가 함께 변화할 때의 영향에 해당한다.
= '교육연수 단독 효과'와 '근속연수 단독 효과'의 합을 초과하는 부분.
즉, 학력이 1년 변화하고 근속연수가 1년 변화했을 때, 월급은,
(𝛽₁+𝛽₃ 근속연수) + (𝛽₂+𝛽₃ 교육연수) + 𝛽₃
로 예측할 수 있다.

연습 2: 성과주의와 직원의 동기부여
설문조사를 통해 직원들의 동기부여, 성과주의 도입 여부, 해당 기업에서 교육훈련 등 능력개발을 위한 프로그램이 잘 갖춰져 있는지 등의 변수를 얻었다고 가정해보자.
여기서 다음 두 가지 가설을 검증하고자 합니다.
이러한 가설을 검증하기 위해서는 어떤 식을 추정하면 좋을까요?
가설 1: 성과주의를 도입한 기업의 직원들의 동기부여가 높을 것이다.
가설 2: 성과주의를 도입한 기업 중 직원들의 동기부여가 높은 기업은 역량개발 프로그램이 충실한 기업일 것이다.
사용 가능한 변수는 다음과 같다.
동기부여: 각 기업의 직원들의 동기부여를 5(매우 동기부여가 높다)에서 1(전혀 동기부여가 없다)까지 5단계로 평가한 것이다.
성과주의 더미: 성과주의 도입이 있으면 1, 없으면 0인 더미 변수.
역량개발 더미: 역량개발 프로그램이 충실하면 1, 그렇지 않으면 0을 취하는 더미변수.

연습 2: 성과주의와 직원의 동기부여
가설 1: 성과주의를 도입한 기업의 직원들의 동기부여가 높을 것이다.
동기부여 = 𝑎₀ + 𝛽₁ 성과주의더미
가설 2: 성과주의를 도입한 기업 중 직원들의 동기부여가 높은 기업은 역량개발 프로그램이 충실한 기업일 것이다.
동기부여 = 𝑎₀ + 𝛽₂ 성과주의더미 + 𝛽₃ 능력개발더미 + 𝛽₄ 성과주의더미 x 능력개발더미
동기부여: 각 기업의 직원들의 동기부여를 5(매우 동기부여가 높음)에서 1(전혀 동기부여가 없음)의 5단계로 평가한 것.
성과주의 더미: 성과주의 도입이 있으면 1, 없으면 0인 더미 변수
능력개발 더미: 능력개발 프로그램이 충실하면 1, 그렇지 않으면 0을 취하는 더미 변수

자연대수

변수를 자연대수(natural logarithm, In)로 변환하는 경우
- 설명변수와 피설명변수의 관계가 일직선이 아닌 경우
설명변수가 증가함에 따라 종속변수도 증가하지만 그 증가율이 일정하지 않은 경우 - 변수의 분포가 편향되어 있는 경우
예: 가구당 저축액 - 극단적인 값(대/소)이 포함되어 있는 경우
극단적인 값이 포함된 데이터의 분산을 작게 하기 위해
⇒ 회귀선형의 적합도를 높이기 위해

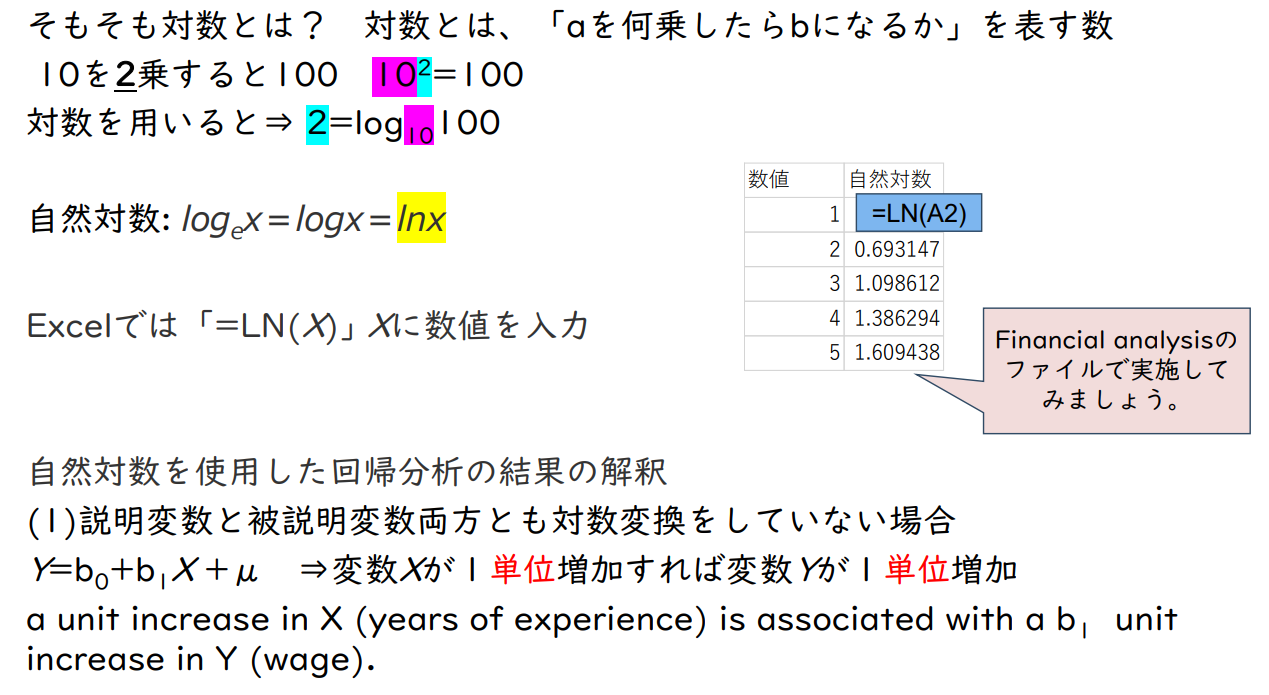
애초에 대수란? 로그는 'a의 몇 배를 곱하면 b가 되는가'를 나타내는 수입니다.
10을 2제곱하면 100 10 ² =100
대수를 이용하면⇒ 2 =log₁₀100
자연대수: logₑx=logx= lnx
엑셀에서는 '=LN(X)은 X에 숫자를 입력'
자연대수를 이용한 회귀분석 결과 해석하기
(1) 설명변수와 피설명변수 모두 대수변환을 하지 않은 경우
Y=b₀ + b₁ X +μ ⇒변수 X가 1 단위 증가하면 변수 Y가 1 단위 증가
X(경력)의 한 단위 증가는 Y(임금)의 b₁ 단위 증가와 관련이 있다.
(2) 피설명변수와 설명변수 모두 대수변환을 한 경우
InY = b₂ + b₃ InX + μ ⇒ 변수 X가 1% 증가했을 때, 변수 Y가 b₃ % 증가
경험치가 1% 증가하면 임금이 b₃% 상승할 것으로 예상할 수 있다.
(3) 피설명변수는 대수변환을 하고, 설명변수는 대수변환을 하지 않은 경우
InY = b₄ + b₅ X + μ ⇒ 변수 X가 1단위 증가하면 변수 Y는 (100 x b₅) % 증가
X가 1단위 증가하면 Y는 100* b₅ % 증가(b₅는 백분율이기 때문에 100을 곱한다).
예 b₅의 추정치가 0.04라고 가정하면, X가 1단위 증가하면 Y는 (100x b5) = 4% 증가
(4) 설명변수는 대수변환을 하고, 피설명변수는 대수변환을 하지 않은 경우
Y = b₆ + b₇
InX + μ ⇒변수 X가 1% 증가했을 때 변수 Y는 1/100 x b₇ 단위 증가
경력 1년이 1% 증가하면 임금이 $(b₇ /100) 증가한다.

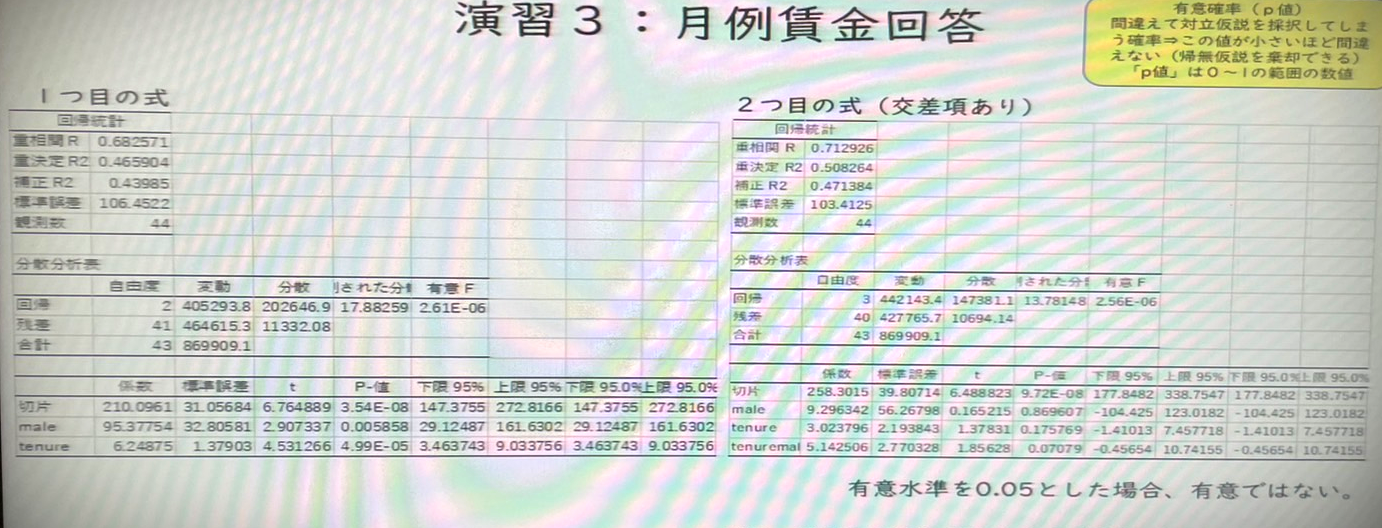
연습 3: 월급
연습3 월별 임금 파일 사용
- 근속년수와 성별의 교차항인 tenuremale(=tenure x male)을 계산한다, 엑셀에서는 '=tenure*male'로 계산할 수 있다.
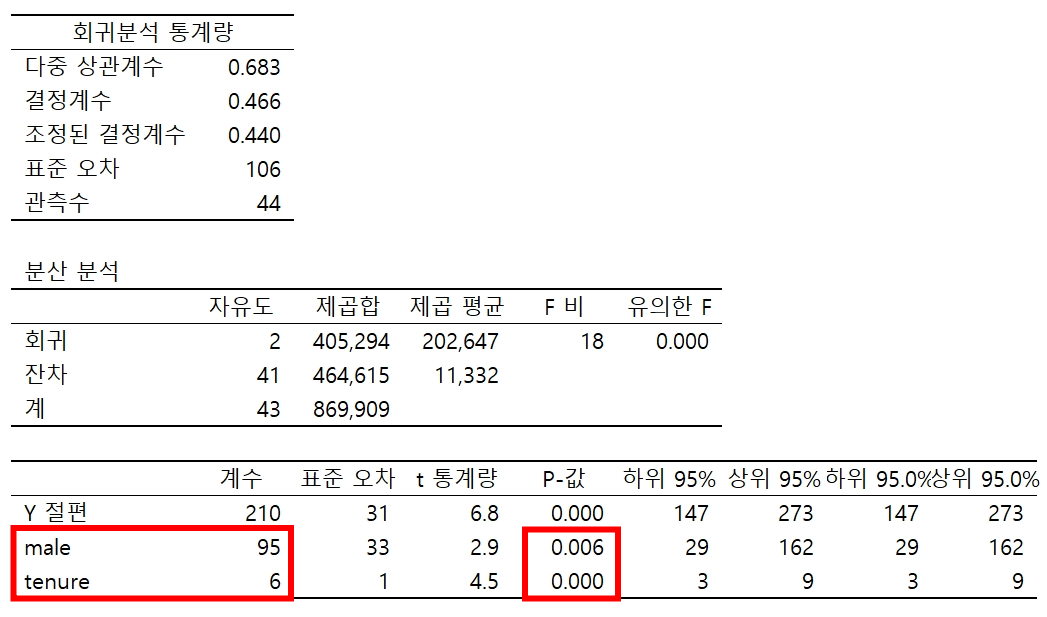
- 피설명변수에 mwage, 설명변수에 male, tenure를 사용하여 분석합니다.
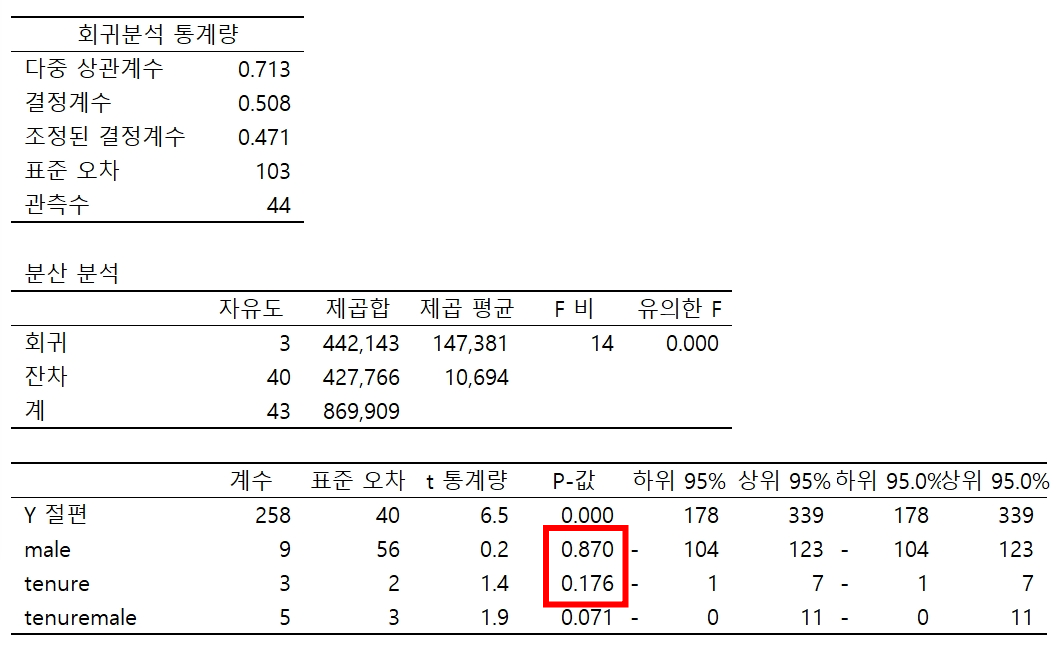
그런 다음 같은 피설명변수로 설명변수에 male, tenure에 tenuremale을 추가하여 분석합니다.
결과를 하나의 표에 정리하고 결과에 대한 의견을 제시하세요.

| 근속연수 | → | 월별임금 | 근속연수 | ↘ | ||
| ↑ | 성별 | → | 월별임금 | |||
| 성별 | 근속연수 x 성별 | ↗ |
모델1 : 남성의 임금이 더 높고, 근속연수가 길수록 더 높다.
모델2 : 근속연수에 따른 임금 상승률은 남성이 더 높습니까?

이산변량 분석

지금까지
- 선형 회귀분석을 최소자승법으로 추정
- 단순 선형회귀 모델 𝑌 = a + 𝛽 𝑋 + μ
- 다중회귀모델 𝑌 = a + 𝛽₁ 𝑋₁ + ⋯ + 𝛽ₖ 𝑋ₖ + μ
| 설명변수 X | → | 종속변수 Y |
| - 연속변수: 근속연수, 교육연수 - 더미변수 : 여성=1, 남성=0 |
- 연속변수: 연속변수: 매출액, 월급, 구매금액, 주가 |
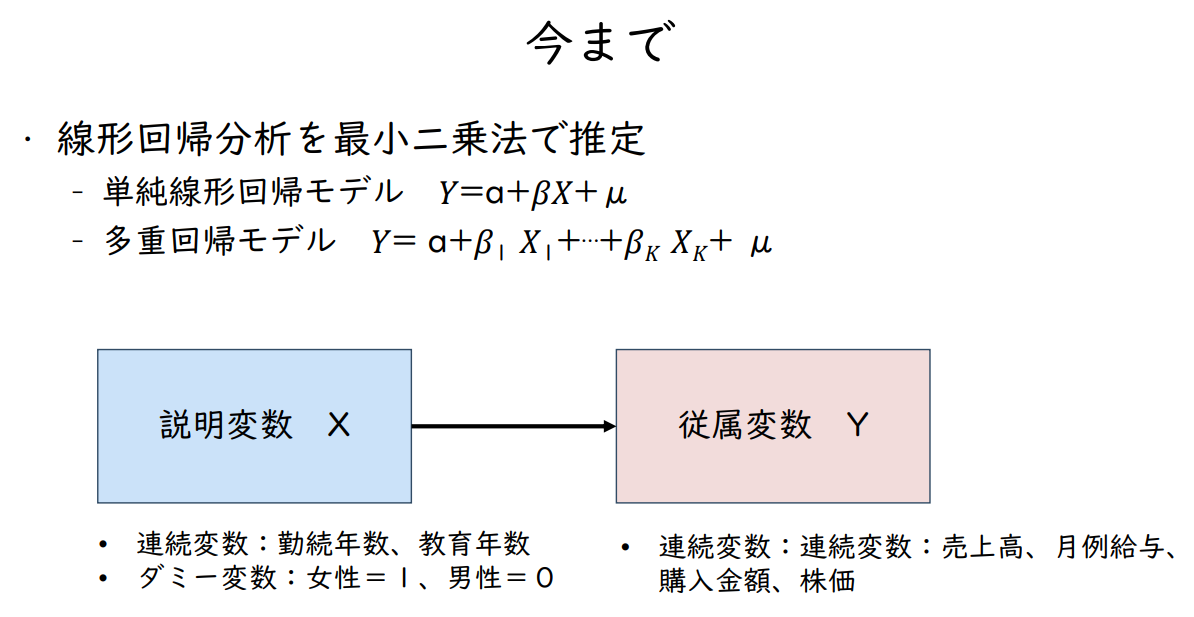
종속변수가 연속변수가 아닌 경우
'한다' 또는 '하지 않는다'라는 이항선택의 예시
- M&A를 한다, 하지 않는다.
- 이직을 한다, 하지 않는다.
- 배당을 증액한다, 하지 않는다.
- 해외에서 신상품을 개발한다, 하지 않는다.
- CEO를 외부에서 영입한다, 하지 않는다.
종속변수가 이항변수(binary)

종속변수가 이항변수(binary)의 분석을 하는 경우...
- 선형회귀모델로도 분석 가능하지만, 선형회귀모델에도 한계가 있다.
- 더 적합한 모델이 있다.
적절한 모형으로 분석
종속변수가 이항변수인 경우 : 이항선택모형(binary choice models)

이항 선택 모델
- 선형 확률 모델(Linear Probability Model: LPM)
선형 확률 모델은 종속 변수가 이항 변수인 선형 회귀 모델 - 이항 로지트 모델 (Logit)
- 이항 프로빗 모델 (Probit)
정규분포에서 얻은 곡선 맞추기

선형 확률 모델(LPM)
최소자승법으로 분석
smartphone = a + b₁ income + μ
장점
- 선형 모델과 유사한 분석
- 계수 해석이 이해하기 쉬움
단점
- 예측값이 1을 초과하거나 마이너스가 될 수 있다.
← 확률은 0에서 1 사이여야 함
스마트폰 보유와 아르바이트로 인한 수입
아르바이트로 인한 수입
1:스마트폰을 가지고 있다
0 : 가지고 있지 않다
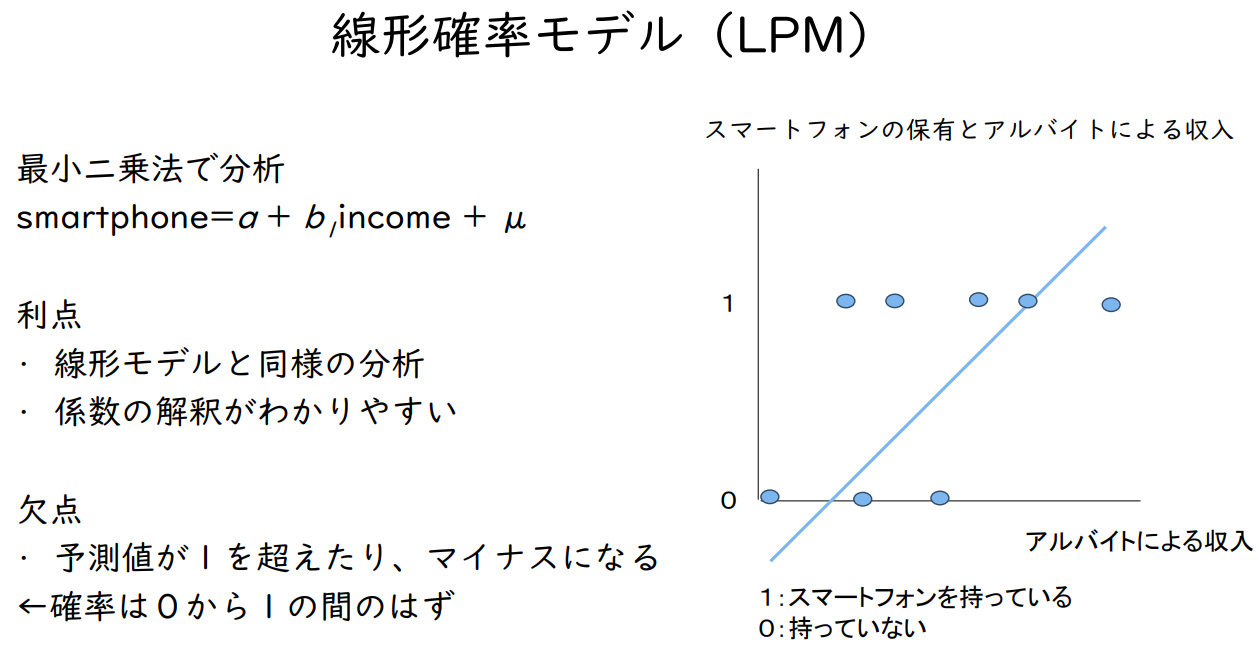
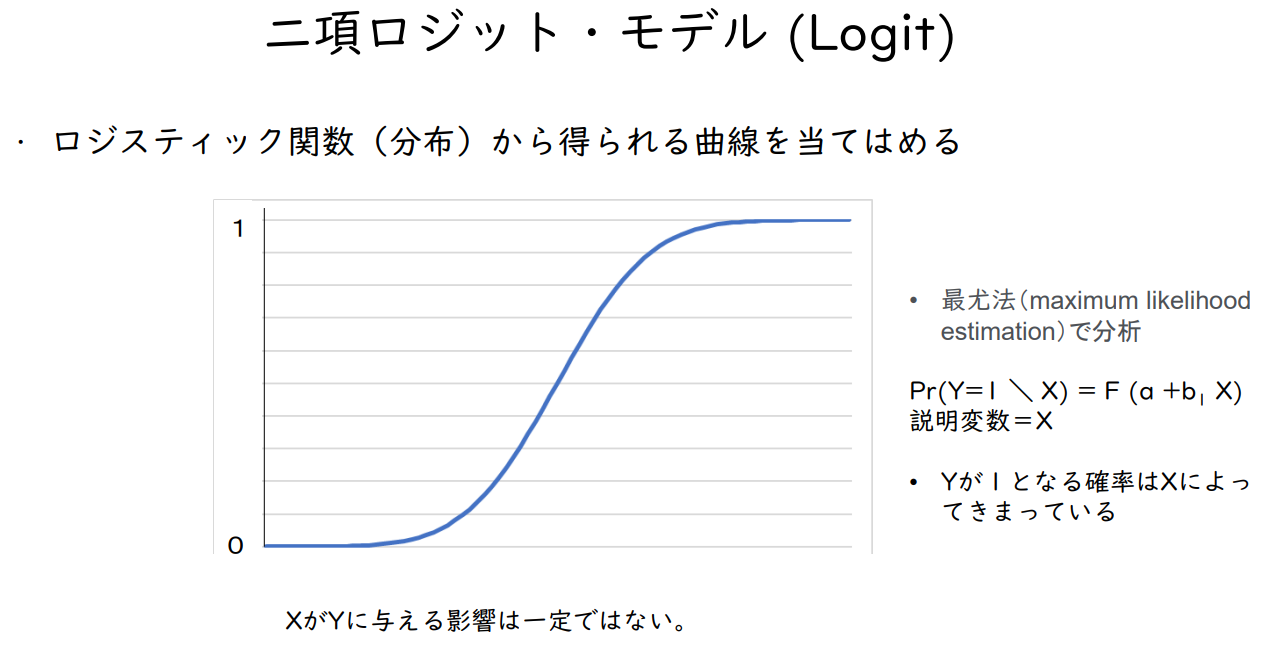
이항 로지트 모델 (Logit)
- 로지스틱 함수(분포)에서 얻은 곡선을 적용하는 방법
- 최대우도법(maximum likelihood estimation)으로 분석
Pr ( Y=1\X ) = F ( a + b₁ X )
설명변수 = X
- Y가 무응답이 될 확률은 X에 의해 결정된다.
X가 Y에 미치는 영향은 일정하지 않다.
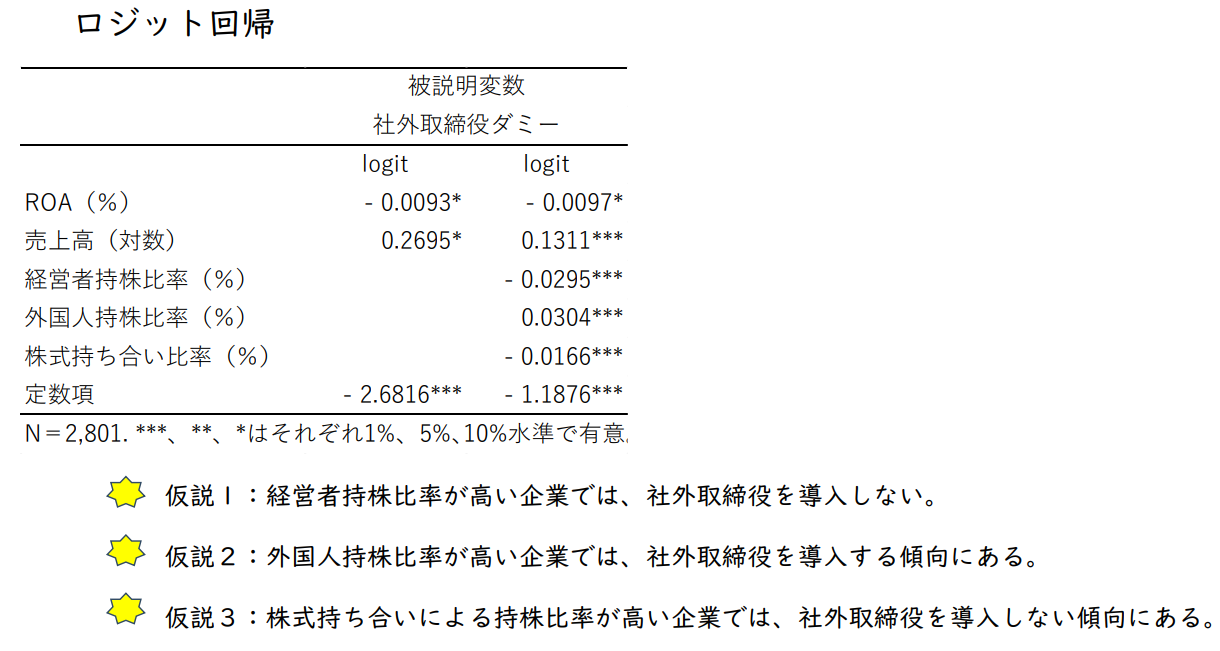
예시: 사외이사 도입 결정요인
가설 1 : 경영자 지분율이 높은 기업에서는 사외이사를 도입하지 않을 것이다.
가설 2 : 외국인 지분율이 높은 기업에서는 사외이사를 도입하는 경향이 있다.
가설 3 : 자사주 보유비율이 높은 기업에서는 사외이사를 도입하지 않는 경향이 있을 것이다.
회귀분석
설명변수 : 경영자 지분율, 외국인 지분율, 자사주 보유비율, ROA, 매출액
피설명변수 : 사외이사 더미
Pr ( Y = 1\X ) = F ( a + b₁ ROA + b₂ 매출액 + b₃ 경영자 지분율 + b₄ 외국인 지분율 + b₅ 자사주 보유율 )

기초통계량
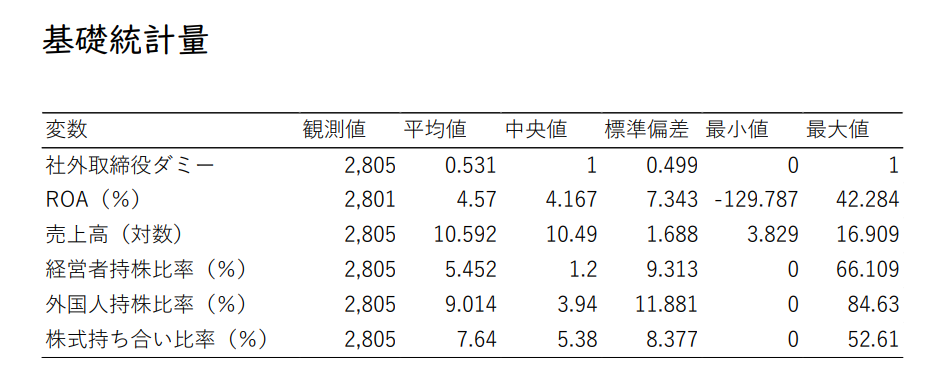
- 가설 1: 경영자 지분율이 높은 기업에서는 사외이사를 도입하지 않을 것이다.
- 가설 2: 외국인 지분율이 높은 기업에서는 사외이사를 도입하는 경향이 있다.
- 가설 3: 자사주 보유비율이 높은 기업에서는 사외이사를 도입하지 않는 경향이 있다.
다항 로지트 모델 (multinominal Logit)
- 2항 선택 로짓 모델에서는 '한다', '하지 않는다'의 2선택
- 3개 이상의 선택지가 있는 경우(순서 없음), 다항 로지트 모델을 사용한다.
예: 집에서 대학까지 통학 수단
- 자전거로 통학한다.
- 버스로 통학한다.
- 전철로 통학한다.

순서 로짓 모델 (Ordered Logit)
- 피설명변수가 순서가 있는 여러 선택지
예) 직원의 직장 만족도
설문조사의 선택지가 다음과 같다.
- 매우 만족한다.
- 다소 만족한다.
- 어느 쪽이라고도 할 수 없다.
- 다소 불만족스럽다.
- 매우 불만이다.

연습4 변수 설정
각 가설을 검증할 때 피설명변수와 설명변수가 어떻게 되는지 간단히 설명하시오.
또한 그 결과를 수식으로 표현하시오.
(1) 우리는 주택담보대출이 어떻게 결정되는지 분석하려고 합니다.
은행에 주택담보대출을 신청한 사람의 정보와 주택담보대출을 받을 수 있었는지를 나타내는 데이터가 있다고 가정하자.
이 데이터를 이용하여 여성이 주택담보대출 심사에서 합리적으로 설명할 수 없는 불리한 대우를 받고 있는지 주목하고 있다.
가설 1: 주택담보대출을 신청했을 때 연봉이 낮은 사람은 거절당할 가능성이 높을 것이다.
가설 2: 여성이 남성보다 거절당할 가능성이 높다.
가설 3: 결혼한 사람은 결혼하지 않은 사람보다 거절당할 가능성이 낮다.

'WBS - 2023 Winter > 기업 데이터 분석' 카테고리의 다른 글
| (기업데이터 #13-14) 패널데이터, 회귀분석 정리 (0) | 2024.01.27 |
|---|---|
| (기업데이터 #9-10) 다중회귀분석 (0) | 2024.01.13 |
| (데이터 #7-8) 연구 방법, 논문 작성 (0) | 2023.12.23 |
| (데이터 #5-6) 데이터 간의 관계 파악 | 상관관계, 인과관계, 단회귀 분석 (0) | 2023.12.16 |
| (데이터 #3-4) 일부 데이터로 전체 추정하기 | 정규분포, 표준정규분포, 확률, 추정과 t검정 (0) | 2023.12.09 |
| (데이터 #1-2) Introduction (0) | 2023.12.04 |



