기업경제학연습 제3회

선형회귀 모델
𝐸 ( 𝑌ᵢ | 𝑋ᵢ ) = 𝛽₀ + 𝛽₁ 𝑋ᵢ
- 회귀모델의 기본 개념은 Y가 어떤 값을 가졌을 때 그 원인을 X에서 찾으려는 것
- X : 영향을 미치는 변수를 설명변수(또는 독립변수)라고 한다.
- Y : 영향을 받는 후자의 변수를 목적변수(또는 종속변수)라고 한다.
- β₀과 β₁을 구하는 방법이 최소자승법(Ordinary Least Square: OLS)이다.

선형회귀 모델
- Y는 데이터 수집 및 기록 시 발생하는 오차 등 X 이외의 요인에도 의존한다.
- 편차는 있지만 두 변수의 관계가 대략 직선으로 표현될 때 다음과 같이 쓸 수 있다.
𝑌ᵢ = 𝛽₀ + 𝛽₁ 𝑋ᵢ + 𝑢ᵢ
단, u는 직선으로부터의 편차를 나타내며 오차항이라고 한다.

중회귀모델(Multiple Regression Analysis)
- k개의 설명변수가 있는 회귀모델의 공식화
𝑌ᵢ = 𝛼 + 𝛽₁ 𝑋₁ᵢ + 𝛽₂ 𝑋₂ᵢ + ⋯ + 𝛽ₖ 𝑋ₖᵢ + 𝑢ᵢ

중회귀분석의 분석 예시
- 2010년경 일본 초등학교 한 학급당 평균 학생 수 28명
→ 이 수치는 OECD 회원국의 21.2명에 비해 많은 수치이다.
→ 2011년부터 문부과학성은 초등학교 1학년 학급 규모(정원)를 40명에서 35명으로 하향 조정했다.
→ 과연 소인수 학급과 아이들의 학력 향상 사이에 인과관계가 있는 것일까?
→ 실증적으로 생각해 본다

소인수 학급의 편익과 비용
- 소인수 학급으로 교사 1인당 학생 수가 상대적으로 적은 것이
- 소인수 학급의 장점
교사의 관심이 아이 한 명 한 명에게 집중되기 쉽다. - 소인수 교육의 비용
인건비가 증가한다

사용하는 데이터
- 데이터는 caschool.csv를 사용함
- 캘리포니아 주 초등학교 5학년의 학군별 시험 결과 평균, 학생 특성 등(1999년 데이터):
- 포함된 데이터
- TESTSCR: 시험의 평균점수 ( ( 국어 성적 + 수학 성적 ) / 2 )
- STR: ( 학생수 / 교원수 ) ← 교원 1인당 학생 수
- EL_PCT: 지구에서 영어를 학습하고 있는 학생 비율
- MEAL_PCT: 급식비 보조를 받는 학생 비율
- CALW_PCT: 학생의 부모가 소득 보조를 받고 있는 학생의 비율

데이터 불러오기
- CSV 파일(comma-separated values)의 경우
caschool <- read.csv ( " caschool.csv " , header = TRUE )

분석 절차
- 데이터에서 기술통계(평균, 표준편차 등)를 정리한다.
- 산점도 등을 사용하여 중요한 변수 간의 관계를 시각적으로 파악한다.
- 회귀분석을 통해 분석의 초점이 되는 변수들 간의 관계를 평가한다.
- 통제 변수를 추가하여 결과의 견고성을 확인한다.

학급 규모, 성적에 관한 기술 통계
- 주목하는 변수의 기술통계(평균, 최대, 최소, 표준편차 등)
'교사 1인당 학생 수'와 '수학 및 국어 점수' 점수의 평균값'
에 관한
- 최소값 | 하위 25% | Median | 평균 | 하위 75% | 최대값
- 표준편차

학급 규모, 성적에 관한 기술 통계
summary ( caschool $ str ) #기술통계
sd ( caschool $ str ) #표준편차

학급 사이즈(선생님 1명당 학생 수)의 기술통계
summary ( caschool $ str ) #기술통계
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
| 14.00 | 18.58 | 19.72 | 19.64 | 20.87 | 25.80 |
sd ( caschool $ str ) #표준편차
1.891812


성적 기술통계
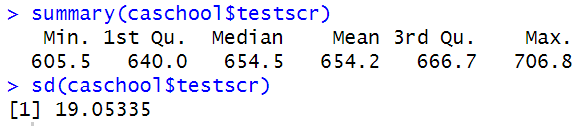
summary ( caschool $ testscr ) #기술통계
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
| 605.6 | 640.0 | 654.4 | 654.2 | 666.7 | 706.8 |
sd ( caschool $ testscr ) #표준편차
19.053

학급 규모와 성적의 관계: 상관관계와 산포도 작성하기
- ' 교사 1인당 학생 수 ' ← 학급규모의 대리 변수
' 수학・국어 점수의 평균값 ' ← 성적 - 상관 계수
cor ( caschool $ str , caschool $ testscr )
-0.2263628
→ 음의 상관관계(단, 그다지 큰 값은 아님)


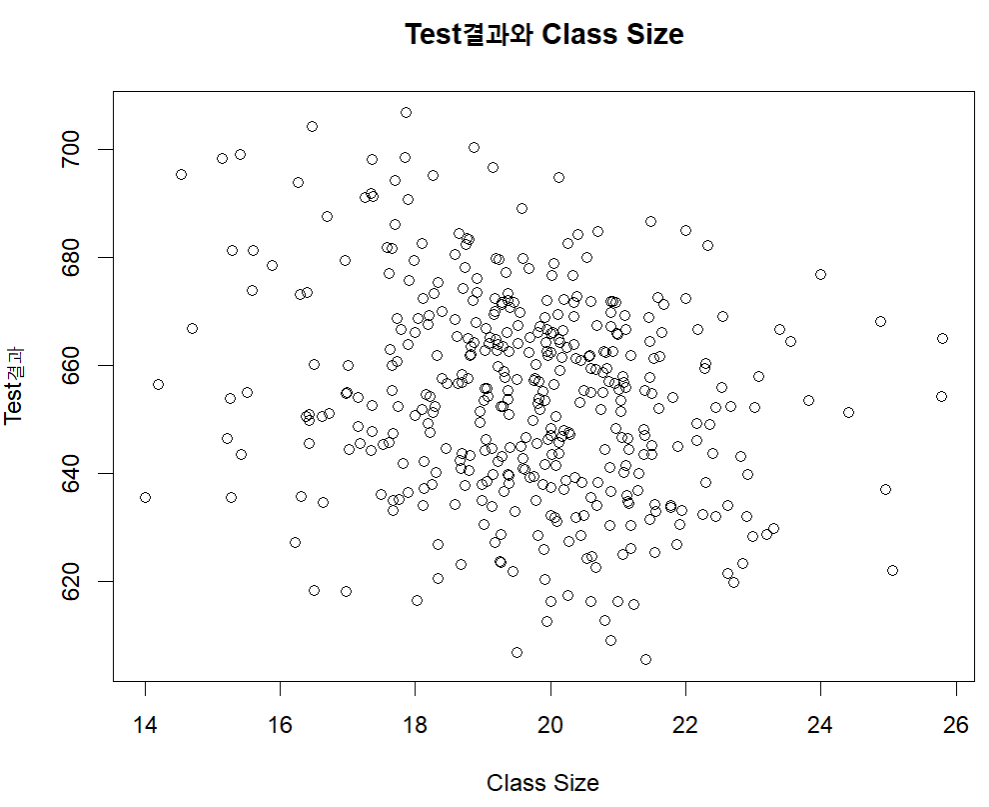
plot ( caschool$str , caschool$testscr ,
main = "Test 결과와 Class Size" ,
xlab = "Class Size" ,
ylab = "Test 결과" )


Test 결과와 Class Size
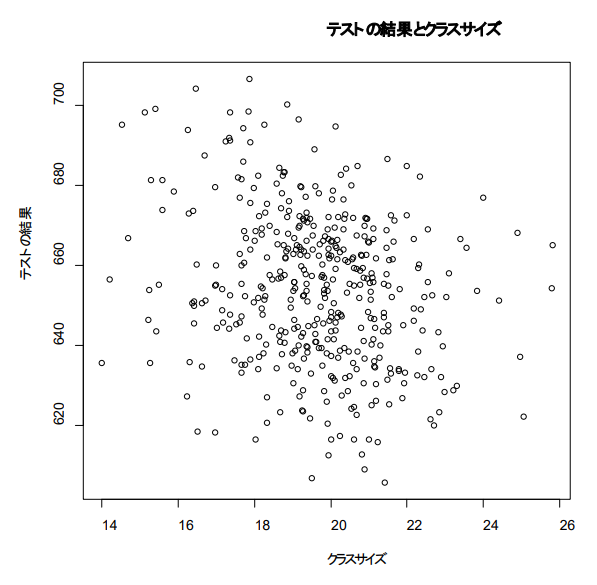
ggplot2를 이용한 그래프 작성
- R은 다양한 패키지를 이용하여 기능을 확장한다.
- 패키지에는 함수, 데이터, 설명용 문장 등이 포함되어 있다.

ggplot2를 이용한 그래프 작성
- tidyverse : 공통된 생각으로 만들어진 다양한 패키지의 집합체
- tidyverse를 설치하면 한 번에 많은 패키지를 설치할 수 있다.
gplot2, tibble, tidyr, readr, purrr, and dplyr packages
install.packages ( " tidyverse " )
library ( tidyverse )

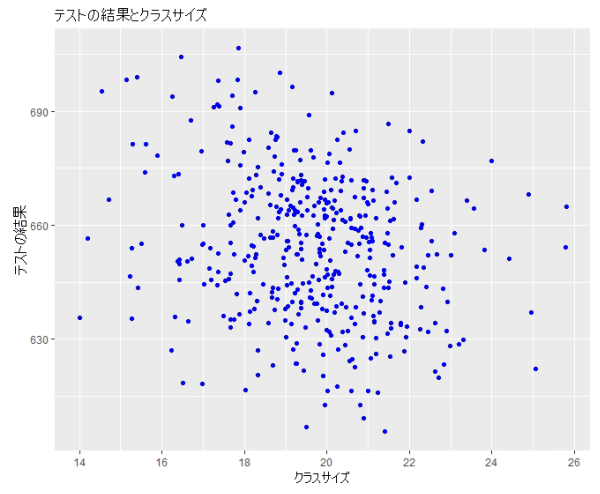
ggplot을 사용하는 경우
ggplot ( data = caschool )
+ geom_point ( mapping = aes ( x = str , y = testscr ) , color = "blue" )
+ labs ( x = 'Class Size', y = 'Test 결과' )
+ labs ( title = 'Test 결과와 Class Size' )
_point : 산포도


Test 결과와 Class Size
추정 모델
- 다음 추정 모델
𝑇estscrᵢ = 𝛽₀ + 𝛽₁ × 𝑆𝑇𝑅ᵢ + 𝑢ᵢ
을 예로 들면
→ 귀무가설로 무엇을 가정할 수 있을까?

귀무가설
우리가 분석의 대상으로 삼은 가설은
"학급 규모가 작을수록 시험 성적이 좋다"
→ 귀무가설 : "학급 규모는 시험 성적에 영향을 미치지 않는다"
H₀ : 𝛽₁ = 0

최소자승법
- 𝛽에 대해 ( 𝛽^₀, 𝛽^₁ )을 추정하고, 그 값을 이용하여 각 X에 대한 Y의 값을 구할 수 있다.
- ( 𝛽^₀, 𝛽^₁ )을 추정하는 가장 기본적인 방법이 최소자승법(Ordinary Least Square: OLS)이다.
→ "무엇의 제곱을 최소화할 것인가?"
𝑌^ = 𝛽^₀ + 𝛽^₁ 𝑋
→ 위 식에서 계산한 예측치 𝑌^와 실제 Y의 '차이의 제곱'
𝑢ᵢ² = ( 𝑌ᵢ − 𝑌^ᵢ )²
이 최소가 되는 지점을 찾는다.




최소자승법과 잔차
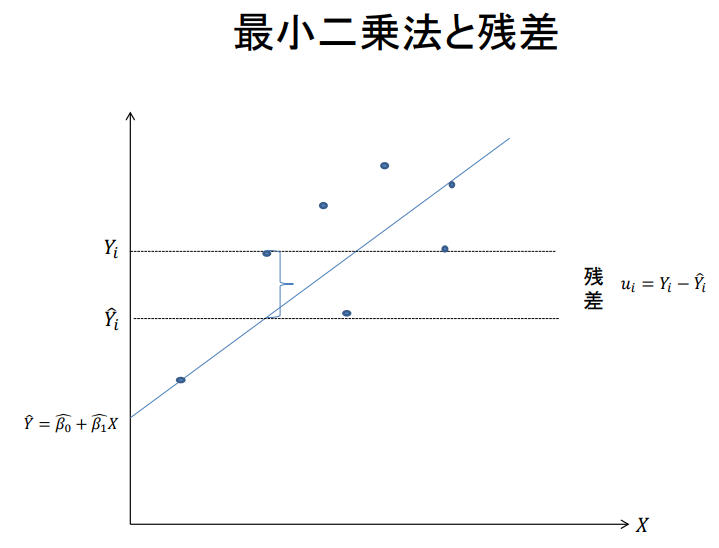
최소자승법
- ( 𝛽^₀, 𝛽^₁ ) 은 다음과 같이 계산된다
𝛽^₀ = 𝑌^ − 𝛽^₁ 𝑋
𝛽^₁ = Σ ( 𝑋𝑖 - 𝑋 ) ( 𝑌𝑖 - 𝑌 ) / Σ ( 𝑋𝑖 - 𝑋 )²


R을 이용한 OLS
𝑇estscr𝑖 = 𝛽₀ + 𝛽₁ × 𝑆𝑇𝑅𝑖 + 𝑢𝑖
- 다음 명령을 입력합니다.
result.ctest1 <- lm ( testscr ~ str , data = caschool )
result.ctest1 = Model 명
testscr = y
str = x
caschool = File 명
summary ( result.ctest1 )

Intercept : 𝛽₀
str : X
Estimate: 계수
Std. Error : 표준오차
t value : t 값
Pr : P값



계수( β₀, β₁ )의 추정치
- ( β₀, β₁ )의 값은 각각 OLS에 따라
| 절편항의 계수 | p값 |
| β₀ = 698.933 | 2e-16 ∗∗∗ |
| 계수의 계수 | p값 |
| β₁ = -2.2798 | 2.78e-06 ∗∗∗ |

추정 결과
- 위의 분석 결과
𝑇estScore = 698.9 − 2.28 × 𝑆𝑇𝑅ᵢ
→ 교원 1인당 학생 수가 1명 증가하면 시험 성적은 -2.28점 하락
→ 교사 1인당 학생 수가 2명 줄어들면 시험 성적은 ( -2 × -2.28 ) = 4.56 포인트 상승 - Adjusted R-squared : 0.04897
→ 조정된 결정계수 = 0.04897

결정 계수에 대해
- 모형의 적합도(fitness)를 나타내는 지표로 결정계수를 사용하는 경우가 많다: 𝑅²
𝑅² = 1 − ∑ (𝑌ᵢ − 𝑌^ᵢ)² / ∑ ( 𝑌ᵢ − 𝑌 )²
X를 설명변수로 하는 단회귀모형에서 설명할 수 있는 Y의 변동 부분의 비율을 나타낸다.



결정 계수에 대해
Multiple R-squared: 0.05124
Adjusted R-squared = 조정된 결정계수 = 0.04897
→ 교사 1인당 학생 수로 성적의 4.8%를 설명할 수 있다.


다중회귀분석
- '학급 규모'가 성적에 부정적인 영향을 미치는 것은 학급이 큰 경우,
영어를 잘 못하는 학생도 포함되어 있기 때문이 아닐까?
→ '영어를 공부하는 학생의 비율'을 변수로 추가할 필요가 있다. - '영어를 공부하는 학생의 비율'이라는 변수를 통제변수라고 한다.
- 회귀분석에서 본래 들어가야 할 변수가 들어가지 않아 결과에 편향이 생길 수 있다.
= '누락변수 편향(Omitted Variable bias)'이라고 한다.

'영어를 공부하는 학생의 비율'과 성적의 관계: 산점도 작성하기
plot ( caschool $ el_pct,
caschool $ testscr,
main = "테스트 결과와 영어 수업 참여율",
xlab = "영어 수업 참여율",
ylab = "테스트 결과" )
cor( caschool $ el_pct , caschool $ testscr )
→ 상관관계를 보면


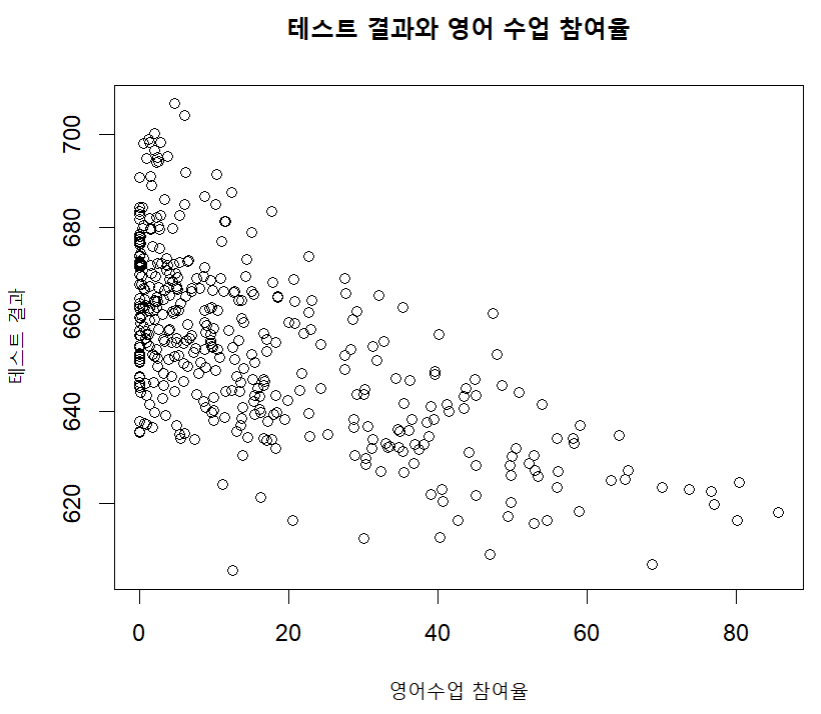
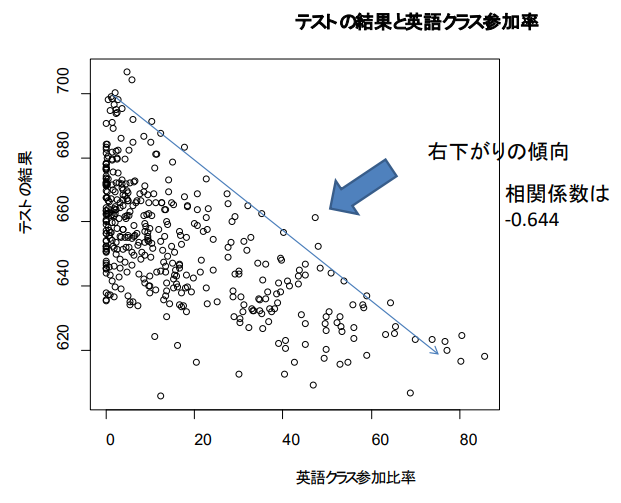
다중회귀
- 다음 추정 Model
𝑇estScore = 𝛽₀ + 𝛽₁ × 𝑆𝑇𝑅ᵢ + 𝛽₂ x PctELᵢ + 𝑢ᵢ
698.9 − 2.28 × 𝑆𝑇𝑅ᵢ
PctEL은 '영어 수업 참여율(%)'
→원 데이터에서는 el_pct 로 표시되어 있습니다.

R을 이용한 OLS
- 다음 명령어를 입력한다.
result.ctest2 <- lm ( testscr ~ str + el_pct , data = caschool )
summary ( result.ctest2 )

결과
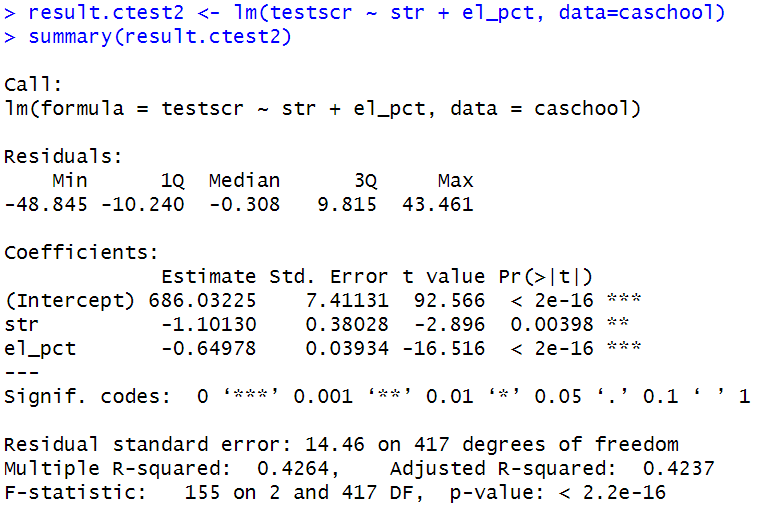


계수( β₀, β₁, β₂ )의 추정치
- ( β₀, β₁, β₂ )의 값은 각각 OLS에 따라
| 절편항의 계수 | p값 |
| 𝛽₀ = 686.032 | 2e−16 ∗∗∗ |
| 계수의 계수 | p값 |
| 𝛽₁ = −1.101 | 0.004 ∗∗ |
| 𝛽₂ = −0.649 | 2e−16 ∗∗∗ |

추정 결과
- 위의 분석 결과로부터
𝑇estScore = 686.0 - 1.101 × 𝑆𝑇𝑅ᵢ - 0.649 x PctELᵢ
- Adjusted R-squared(조정된 결정계수) = 0.423
- F-statistic: 155 on 2 and 417 DF, p-value: 2.2e-16
→ F값 = 155, p-value = 2.2e-16
→ 모든 계수가 0이라는 귀무가설은 기각된다.

추정 결과
- '학급 규모'와 '영어를 공부하는 학생 비율' 두 변수의 계수는 모두 유의미하게 음(-)의 값을 보임.
- 교사 1인당 학생 수가 1명 증가하면 시험 성적은 -1.10 포인트 하락
- 영어를 공부하는 학생의 비율이 1% 증가하면 시험 성적이 -0.65 포인트 하락한다.
- '학급 규모'의 영향력은 단일 회귀분석에 비해 크게 감소( -2.28 → -1.10 )
- 이는 단회귀에서는 다른 변수(이 경우 '영어를 공부하는 학생의 비율')의 영향을 포함한 형태로 추정을 하고 있음을 시사한다.

다중회귀분석
- '학급 규모', '영어를 공부하는 학생의 비율' 외에 통제해야 할 다른 변수가 있을까?
- 가정의 소득수준이 학력에 영향을 미치는 것은 아닐까?
- 소득수준을 통제하는 변수로 두 가지 선택지
1)「급식비가 보조되는 학생의 비율」이다.
2)「학생의 부모에게 공적 소득지원이 이루어지고 있는 비율」.

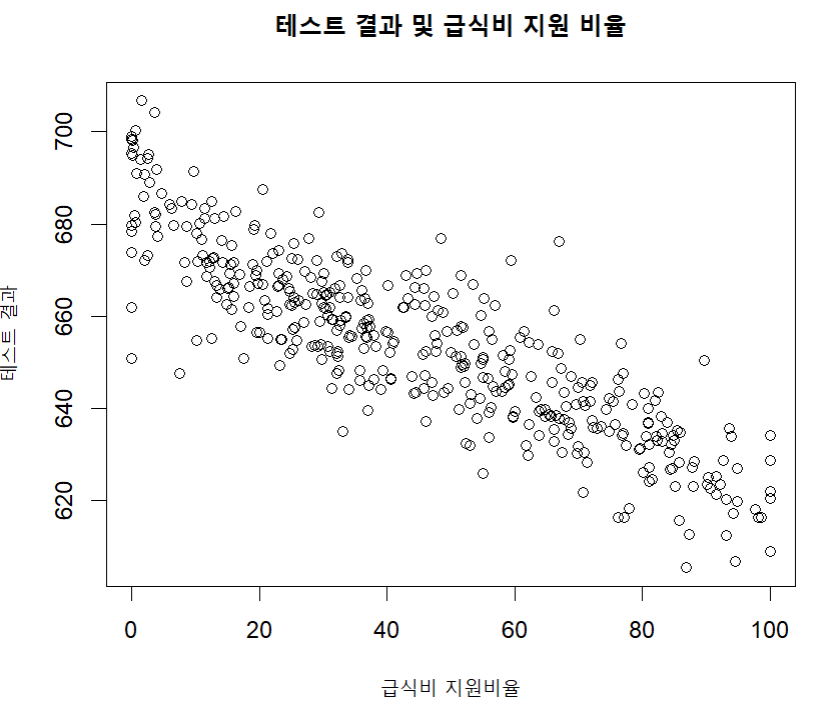
'급식 보조 비율'과 성적의 관계: 산점도 작성하기
plot ( caschool $ meal_pct ,
caschool $ testscr ,
main = " 테스트 결과 및 급식비 지원 비율 " ,
xlab = " 급식비 지원 비율 " ,
ylab = " 테스트 결과 " )
cor ( caschool $ meal_pct , caschool $ testscr )
상관 계수 계산하기



다중회귀
- 다음 추정 모델
𝑇estsc𝑟ᵢ = 𝛽₀ + 𝛽₁ × 𝑆𝑇𝑅ᵢ + 𝛽₂ × PctELᵢ + 𝛽₃ × 𝐿chPct + 𝑢ᵢ
LchPct는 '급식비 보조를 받는 학생의 비율(%)'이다.
→ 원 데이터에서는 meal_pct로 표시됨

R을 이용한 OLS
- 다음 명령을 입력합니다.
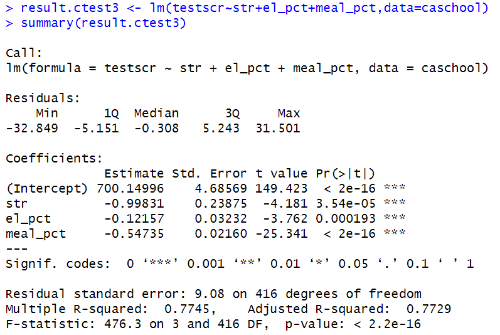
result.ctest3 <- lm ( testscr ~ str + el_pct + meal_pct , data = caschool )
summary ( result.ctest3 )

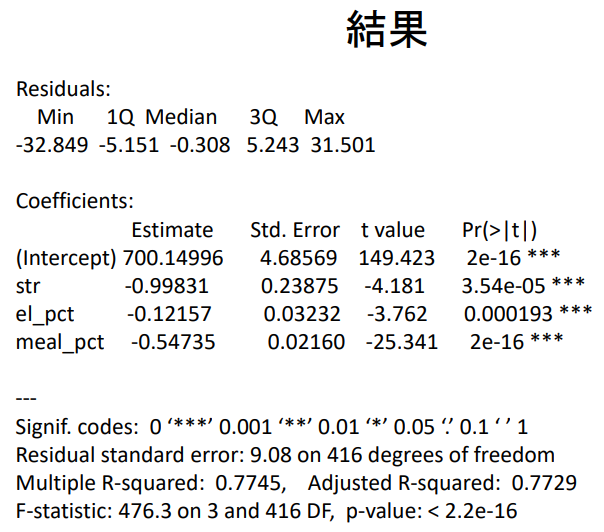
결과

다중회귀
- 추정 모델
𝑇estsc𝑟ᵢ = 700.149 - 0.998 × 𝑆𝑇𝑅ᵢ - 0.121 × PctELᵢ - 0.547 × 𝐿chPct + 𝑢ᵢ
Adjusted R-squared(조정된 결정계수) = 0.772
F-statistic: 476.3 on 3 and 416 DF, p-value: 2.2e-16
→ F값 = 476.3, p-value = 2.2e-16
→ 모든 계수가 0이라는 귀무가설은 기각된다.

추정 결과
- '학급 규모', '영어를 공부하는 학생 비율', '급식비 지원 학생 비율'의 계수는 모두 유의미하게 음(-)의 값으로 나타남
- 교사 1인당 학생 수가 1명 늘어날 때마다 시험 성적은 -0.998점 하락
- 영어를 공부하는 학생 비율이 1% 증가하면 시험 성적은 - 0.121점 낮아진다.
- 급식비 보조를 받는 학생 비율이 1% 증가하면 시험 성적은 -0.547점 하락
→ 부모의 소득이 낮을수록 자녀의 성적이 나빠진다.

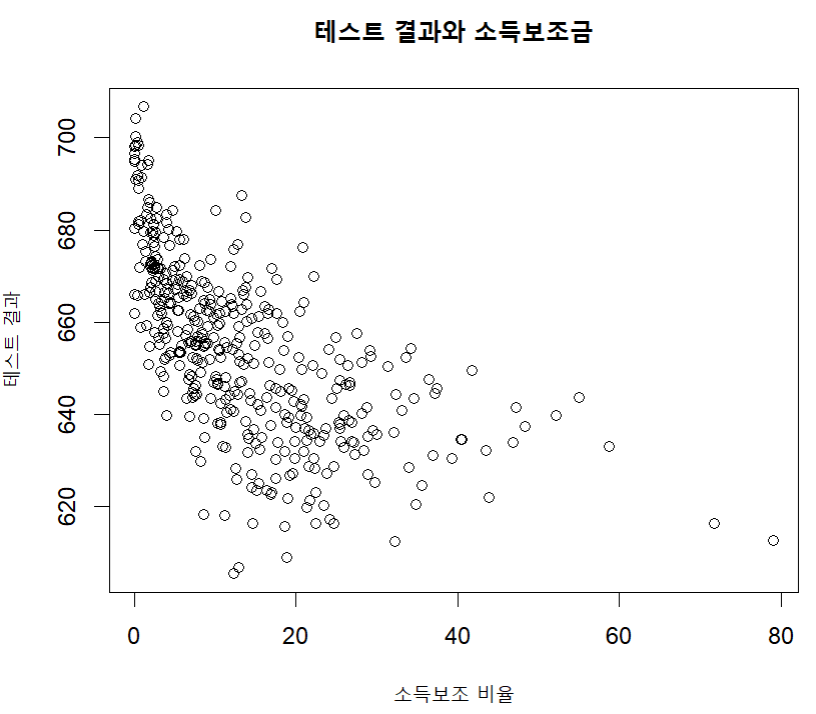
'공적인 소득보조 비율'과 성적의 관계: 산점도 작성하기
plot ( caschool $ calw_pct ,
caschool $ testscr ,
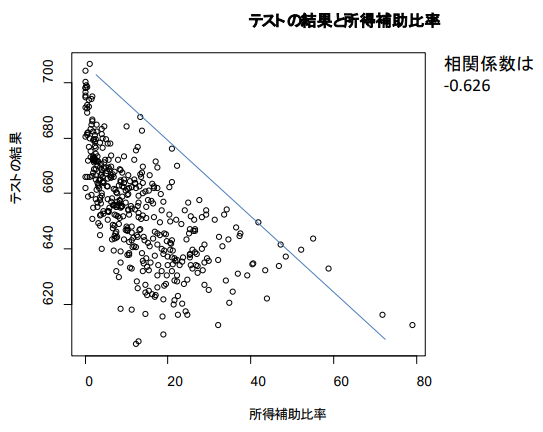
main = " 테스트 결과와 소득보조금 " ,
xlab = " 소득보조 비율 " ,
ylab = " 테스트 결과 " )
cor ( caschool $ calw_pct , caschool $ testscr )
→ 상관관계 계수 계산하기


테스트 결과 및 소득 보조 비율
다중회귀
- 다음 추정 모델
𝑇estsc𝑟ᵢ = 𝛽₀ + 𝛽₁ × 𝑆𝑇𝑅ᵢ + 𝛽₂ × PctELᵢ + 𝛽₃ × 𝐼chPctᵢ + 𝑢ᵢ
IncPct 는 '학생의 부모에게 공적 소득 지원이 이루어지고 있는 비율(%)'입니다.
→ 원 데이터에서는 calw_pct 로 표시되어 있다.

R을 이용한 OLS
- 다음 명령을 입력합니다.
result.ctest4 <- lm ( testscr ~ str + el_pct + calw_pct , data = caschool )
summary ( result.ctest4 )

결과
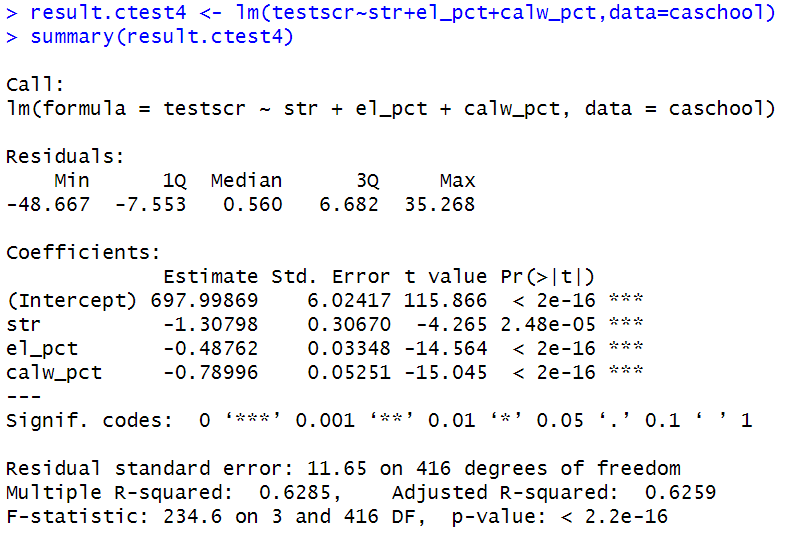


다중회귀
- 추정 모델
𝑇estsc𝑟ᵢ = 697.998 - 1.307 × 𝑆𝑇𝑅ᵢ - 0.487 × PctELᵢ - 0.789 × 𝐼chPctᵢ + 𝑢ᵢ - Adjusted R-squared(조정된 결정계수) = 0.6259
F-statistic: 234.6 on 3 and 416 DF, p-value: 2.2e-16
→ F값 = 234.6, p값 = 2.2e-16
→ 모든 계수가 0이라는 귀무가설은 기각된다.

추정 결과
- '학급 규모', '영어를 공부하는 학생 비율', '학생의 부모에게 공적 소득지원이 이루어지는 비율'의 계수는 모두 유의미한 음(-)의 값을 보임.
- 교사 1인당 학생 수가 1명 늘어날 때마다 시험 성적은 -1.31점 하락
- 영어를 공부하는 학생 비율이 1% 증가하면 시험 성적이 -0.488점 하락
- 학생의 부모에게 공적 소득지원이 이루어지는 비율이 1% 증가하면 시험 성적은 -0.790 포인트 하락한다.
→ 부모의 소득이 낮을수록 자녀의 성적이 나빠진다. - 부모의 소득수준을 포착하는 대리변수로 다른 변수를 사용하면 계수의 크기도 조금 달라진다.

다중회귀
- 다음 추정 모델
𝑇estsc𝑟ᵢ = 𝛽₀ + 𝛽₁ × 𝑆𝑇𝑅ᵢ + 𝛽₂ × PctELᵢ + 𝛽₃ × 𝐿chPctᵢ + 𝛽₄ × 𝐼chPctᵢ + 𝑢ᵢ
→ 소득수준을 통제하는 변수를 동시에 두 개 모두 넣어 추정한다.

R을 이용한 OLS
- 다음 명령을 입력합니다.
result.ctest5 <- lm ( testscr ~ str + el_pct + meal_pct + calw_pct , data = caschool )
summary ( result.ctest5 )

결과



다중회귀
- 다음 추정 모델
𝑇estsc𝑟ᵢ = 700.391 - 1.014 × 𝑆𝑇𝑅ᵢ - 0.129 × PctELᵢ - 0.528 × 𝐿chPct - 0.047 × 𝐼chPctᵢ + 𝑢ᵢ - Adjusted R-squared(조정된 결정계수) = 0.7727
F-statistic: 357.1 on 4 and 415 DF, p-value: 2.2e-16
→ F값 = 357.1, p값 = 2.2e-16
→ 모든 계수가 0이라는 귀무가설은 기각된다.

추정 결과
- '학급 규모', '영어를 공부하는 학생 비율', '학생의 부모에게 공적 소득 지원이 제공되는 비율'의 계수는 유의미한 음의 상관관계를 보임
- 교사 1인당 학생 수가 1명 늘어날 때마다 시험 성적은 1.01점 하락
- 영어를 공부하는 학생 비율이 1% 증가하면 시험 성적은 -0.129점 하락
- 급식비 보조를 받는 학생 비율이 1% 증가하면 시험 성적은 -0.528점 하락
→ 부모의 소득이 낮을수록 자녀의 성적이 나빠진다.

추정 결과
- 부모의 소득수준을 파악하는 두 번째 변수인 '학생의 부모에게 공적 소득지원이 이루어지고 있는 비율'의 계수는 유의하지 않다.
| 계수 -0.047 | t값 -0.785 | p값 0.432 |
→ 같은 성격을 가진(특히 상관관계가 높은) 여러 변수를 동시에 설명변수로 사용할 경우
유의성이 낮아지는 경우가 있으므로 주의 필요
→ 두 변수의 상관관계 계수는 0.73

결과의 정리
- 회귀분석 결과를 정리하여 표로 만들려면 stargazer라는 패키지가 유용합니다.
# install.packages ( " stargazer " )
library ( stargazer )
- 결과를 자동으로 정리해줌

stargazer ( result.ctest1, result.ctest2, result.ctest3, result.ctest 4,
keep.stat = c ( ' n ' , ' adj.rsq ' , ' f ' ) ,
df = FALSE,
type = " text ",
out = " results_lec3_1.txt ")
keep.stat = c ( 'n', 'adj.rsq', 'f' ) : 아래 값은 표와 같다.
n : 샘플 수
adj.rsq : 조정된 결정계수
f : F값


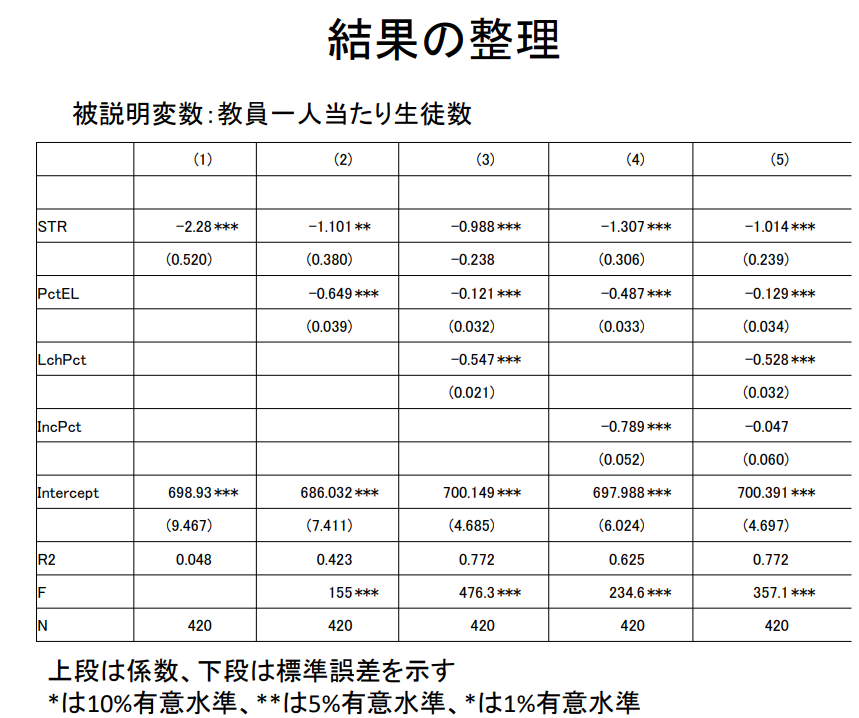
설명변수: 교사 1인당 학생 수
| (1) | (2) | (3) | (4) | (5) | |
| STR | -2.28 *** | -1.101 ** | -0.988 *** | 1.307 *** | -1.014 *** |
| (0.520) | (0.380) | -0.238 | (0.306) | (0.239) | |
| PctEL | -0.649 *** | -0.121 *** | -0.487 *** | -0.129 *** | |
| (0.039) | (0.032) | (0.033) | (0.034) | ||
| LchPct | -0.547 *** | -0.528 *** | |||
| (0.021) | (0.032) | ||||
| IncPct | -0.789 *** | -0.047 | |||
| (0.052) | (0.060) | ||||
| Intercept | 698.93 *** | 686.032 *** | 700.149 *** | 697.988 *** | 700.391 *** |
| (9.467) | (7.411) | (4.685) | (6.024) | (4.697) | |
| R2 | 0.048 | 0.423 | 0.772 | 0.625 | 0.772 |
| F | 155 *** | 476.3 *** | 234.6 *** | 357.1 *** | |
| N | 420 | 420 | 420 | 420 | 420 |
상단은 계수, 하단은 표준오차를 나타냄.
*는 10% 유의수준, **는 5% 유의수준, *는 1% 유의수준
'WBS - 2023 Fall > 기업경제학 연습' 카테고리의 다른 글
| (기업경제 #9) Matching (0) | 2023.12.06 |
|---|---|
| (기업경제 #8) 로지트 모델(Logit Model)과 프로빗 모델(Probit Model) (0) | 2023.11.29 |
| (기업경제 #7) DID | Difference-in-Difference (차이의 차이 분석) (0) | 2023.11.16 |
| (기업경제 #6) 패널 분석 (Panel data analysis) (0) | 2023.11.09 |
| (기업경제 #5) 더미 변수를 이용한 분석 (0) | 2023.11.02 |
| (기업경제 #4) 이상치 처리 | 선형 회귀 모델(2) (0) | 2023.10.26 |
| (기업경제 #2) (0) | 2023.10.12 |
| (기업경제 #1) (0) | 2023.10.05 |



