기업경제학연습 제6회

오늘의 예정
- 패널 분석 (Panel data analysis)

시계열 데이터
- 특정 경제주체에 대해 일정한 시간 간격으로 수집한 정보를 시계열 데이터라고 한다.
- 일반적으로 시계열 데이터의 빈도(간격)는 일정하며, 연, 반기, 분기, 월 등으로 수집된 것
- 시계열 데이터는 동일한 주체에 대한 변수의 '변화'를 추적한다.


Cross-Section Data(횡단면 데이터)
- 여러 경제주체의 '특정 시점'의 정보를 횡단면적으로 수집한 것을 Cross-Section Data(횡단면 데이터)라고 한다.
- 시점은 고정되어 있지만, 대상 범위에 따라 국가-지역-지방자치단체 등의 지점,
기업-학교 등 조직, 연령-학력 등 속성 속에서 각 변수가 어떻게 분포되어 있는지 파악할 수 있다. - 횡단면 데이터는 각 변수의 경제주체 간 '차이'를 비교한다.

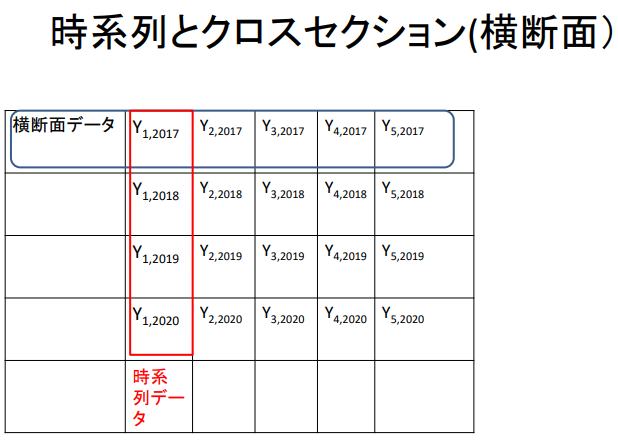
시계열과 Cross-Section(횡단면)
| 횡단면 Data | Y1 , 2017 | Y2 , 2017 | Y3 , 2017 | Y4 , 2017 | Y5 , 2017 |
| Y1 , 2018 | Y2 , 2018 | Y3 , 2018 | Y4 , 2018 | Y5 , 2018 | |
| Y1 , 2019 | Y2 , 2019 | Y3 , 2019 | Y4 , 2019 | Y5 , 2019 | |
| Y1 , 2020 | Y2 , 2020 | Y3 , 2020 | Y4 , 2020 | Y5 , 2020 | |
| Y1 , 2021 | Y2 , 2021 | Y3 , 2021 | Y4 , 2021 | Y5 , 2021 | |
| 시계열 Data |
패널 데이터란?
- 동일 경제주체(기업, 개인, 정부 등)에 대해 여러 시점의 데이터를 수집한 것
- 모든 경제주체, i, 에 대해 모든 시점이 모두 갖추어져 있을 때: balanced panel data
- 어떤 경제주체에 대해 일부 시점의 데이터가 부족한 경우: unbalanced panel data
패널 데이터란?
- 시계열 보고와 횡단면 방향의 정보를 모두 포함하고 있기 때문에
패널 데이터의 정보량이 풍부하고, 표본의 크기도 크다. - 동일한 경제주체를 추적하고 있기 때문에 큰 정책변화가 발생하거나 금융위기와 같은 경제충격 또는
동일본 대지진과 같은 비경제적 충격이 발생했을 때,
그 충격 전후에 행동과 사건이 어떻게 변화했는지를 파악할 수 있다. - 일반적으로 실증분석에 사용되는 데이터는 적당한 변이(variation)가 있는 것이 바람직하다.
→ 패널 데이터는 시간과 횡단면 모두에서 변이를 이용할 수 있다.

패널 데이터 이미지
| 기업ID | 연 | ROE | 경영자보수 (10만) |
| 1 | 2017 | 14.1 | 1,095 |
| 1 | 2018 | 14.5 | 1,050 |
| 1 | 2019 | 14.3 | 1,100 |
| 2 | 2017 | 5.9 | 578 |
| 2 | 2018 | 6.1 | 590 |
| 2 | 2019 | 6.0 | 610 |

패널 분석에 대하여
- 이제 다음과 같은 한 설명변수의 추정식을 생각해 보자.
yᵢₜ = β xᵢₜ + u ᵢₜ
u ᵢₜ = μ ᵢ + εᵢₜ
→ yᵢₜ = β xᵢₜ + [ μᵢ + εᵢₜ ] - t 는 기간을 나타내며, t = 1 , ... , T
- i 는 경제주체(기업, 개인 등)의 수를 나타내며, i = 1 , ... , N
- 오차항 u 는 두 개의 오차항인 μ 와 ε 의 합
- μᵢ : 확률변수이자 각 경제주체 고유의 효과(고정효과)를 나타낸다.
- εᵢₜ : 표준 OLS의 가정을 만족하는 오차항

패널 분석의 장점
- 경제주체(기업, 개인 등) 간 관찰할 수 없는(unobservable) 특성의 차이(이질성)가 미치는 영향을 통제할 수 있다.
→ 관측할 수 없는 요인이 결과에 영향을 미치는 경우, 패널 분석을 통해 누락변수 편향의 문제를 해결할 수 있다.

변량효과 모델과 고정효과 모델
- 고정효과와 설명변수의 관계는 다음과 같은 두 가지 가능성이 있다.
COV ( μᵢ , xᵢₜ ) = 0
COV ( μᵢ , xᵢₜ ) ≠ 0
→ 전자의 경우 변량효과모형(Random Effect Model)
→ 후자의 경우에는 고정효과모형(Fixed Effect Model)을 추정모형으로 채택해야 한다.

고정효과 모델(Fixed Effect Model)
yᵢₜ = β xᵢₜ + uᵢₜ
uᵢₜ = μᵢ + εᵢₜ
→ yᵢₜ = β xᵢₜ + μ ᵢ + εᵢₜ
- 설명변수와 오차항의 고정효과 부분이 상관관계
⇒ OLS를 이용하여 매개변수를 추정하는 것은 일치성을 만족하지 못하기 때문에 부적절함
⇒ '고정효과모형(추정)'이라는 기법을 이용하여 파라미터 β를 추정할 수 있다.



고정효과 모델(Fixed Effect Model)
- 이제 각 i에 대해
yᵢₜ = βxᵢₜ + uᵢₜ
uᵢₜ = μᵢ + εᵢₜ
기간 동안의 평균값을 계산합니다.
yᵢ = βxᵢ + uᵢ
uᵢ = μᵢ + εᵢ
yᵢ = ( Σⱼyᵢₜ ) / T ,
xᵢₜ = Σₜ ( xᵢₜ / T ) ,
uᵢₜ = Σₜ ( uᵢₜ / T )

고정효과 모델(Fixed Effect Model)
- 각 yᵢₜ와 y의 평균값의 차이를 xᵢₜ와 x의 평균값의 차이로 회귀
yᵢₜ - yᵢ = β ( xᵢₜ - xᵢ ) + z ᵢₜ
zᵢₜ = uᵢₜ - uᵢ = ε ᵢₜ - ε ᵢ
→ 고정효과(μᵢ)가 사라짐
→ 시간에 따라 변화하는 오차항 ε가 설명변수와 상관관계가 없는 경우 OLS로 추정 가능
→ 고정효과모형이란 피설명변수의 경제주체별 평균값에서 벗어난 부분을
설명변수의 경제주체별 평균값에서 벗어난 부분으로 회귀하는 것


고정효과 모델(Fixed Effect Model)
- '추가적인 변수를 관찰하지 않고도 결측변수 편향을 피할 수 있다'는 점이 중요하다.
- 필요한 가정은 '누락변수 편향을 가져오는 요소는 시간에 따라 일정하다'라는 점
→ 이 가정이 항상 성립하는 것은 아니지만, 누락변수 편향이 부분적으로나마 해결될 수 있다는 것은
패널데이터를 이용한 분석의 큰 장점


변량효과모델(Random Effect Model)
- 변량효과 모형의 경우 COV ( μᵢ , xᵢₜ ) = 0 이므로 일반적인 OLS의 가정을 충족할 수 있으며,
패널 데이터를 사용함으로써 얻을 수 있는 장점은 특별히 없다. - 패널 데이터를 사용한다는 것을 의식하지 않고 OLS로 추정을 하면 된다.
- 단, t ≠ s 일때 COV ( uᵢₜ , uᵢₛ ) ≠ 0 이므로, 오차항 간의 계열 상관관계에 견고한 표준오차를 사용할 필요가 있다.
→ '변량효과 모델'을 선택하면 이 점은 수정된다 (이를 위해 일반화 최소자승법을 사용한다).

고정효과 모델인가 변량효과 모델인가?
- 고정효과 모델의 추정량은 진정으로 사용해야 할 모델이 고정효과 모델인지 변량효과 모델인지에 관계없이
적절한 추정량 - 변량효과모형의 추정량은 진정으로 사용해야 할 모형이 변량효과모형일 경우에만 적절한 추정량
- 변량효과모형과 고정효과모형의 추정량 크기가 비교적 가까우면 '변량효과모형',
두 추정량 크기가 크게 다르면 '고정효과모형'을 채택해야 한다.
⇒ 이 점을 검정하기 위해 'Hausman 검정'이 자주 사용된다.

고정효과 모델인가 변량효과 모델인가?
- 'Hausman 검정'은 통계적 검정이기 때문에 항상 올바른 판단을 내리는 것은 아니다.
⇒ 어느 정도의 확률로 잘못된 판단을 내린다.
⇒ 고정효과 모형을 채택해야 할 곳에 변량효과 모형을 채택하는 경우,
적절하지 않은 변량효과 모형의 사용으로 인해 본래 유의하지 않은 효과가 유의하게 될 가능성도 지적되고 있다
(Guggenberger(2010, Journal of Econometrics 156 337-343).
패널 데이터 분석에서는 일반적으로 고정효과 모형을 채택하는 것이 더 적절한 경우가 많다.

시간 효과 도입
- 지금까지는 시간에 따라 일정하지만 관찰 개체마다 다른 고정효과에 대해 논의했다.
- 다음으로 관찰 개체 간에는 일정하지만 시간에 따라 변화하는 '시간효과'를 소개하고자 한다.
- 아래는 시간효과 모델이며, 시간효과는 첨자가 i 가 아닌 t 라는 점이 중요하다.
yᵢₜ = β xᵢₜ + λ ₜ + εᵢₜ

시간 효과 도입
- 시간효과를 모형에 포함시키는 이유는 고정효과의 경우와 마찬가지로 누락변수의 편향성을 피하기 위함이다.
- 경제학 실증분석에서는 거시경제의 영향이나 국가 차원의 제도적 변화의 영향을 통제하기 위해
시간효과를 모형에 포함시키는 경우가 많다.

시간 효과(Time Effect)
- 이제 각 시점 t 에서
yᵢₜ = β xᵢₜ + λₜ + εᵢₜ
의 샘플 간 평균값을 계산한다.
yₜ = β xₜ + εₜ
yₜ = ( Σⱼ yᵢₜ ) / N ,
xₜ = Σᵢ ( xᵢₜ / N ) ,
εₜ = Σᵢ ( εᵢₜ / N )

시간 효과(Time Effect)
- 각 yᵢₜ와 y의 평균값의 차이를 xᵢₜ와 x의 평균값의 차이로 회귀
yᵢₜ - yₜ = β ( xᵢₜ - xₜ ) + εᵢₜ - εₜ
→ 시간효과가 사라짐
→ OLS로 추정 가능

시간 효과와 시간 더미
- 시간 효과의 제어는 시간 더미(time dummy)를 넣은 모델로도 표현할 수 있다.
yᵢₜ = λ₁ T 1 ᵢₜ + ... + λₜ T T ᵢₜ + β xᵢₜ + εᵢₜ
예. T1 = 2020, T2 = 2021, T3 = 2022...
T1은 t = 1 이면 1, 그 외의 시간에는 0을 취한다.
TT는 t = t 일 때만 1, 그 외에는 0을 취한다.
예) 2020년만 1이고, 그 외에는 0을 취하는 더미 변수
- 이 모델을 OLS 추정하기

R을 이용한 패널 데이터 모델 추정
- 패널 데이터 모델을 분석하기 위한 R의 '패키지'로는 plm 이 있습니다.
install.packages ( " plm " )

교통사고 사망과 알코올 세금
- 가설: 술에 세금을 부과하면 음주 교통사고 사망자 수를 줄일 수 있을까?
- 데이터: 1982-1988년
- 미국 각 주의 교통사고로 인한 사망자 수
- 맥주 세율 등
- 데이터 파일은
fatalitydata <- read.csv ( " fatality.csv " )
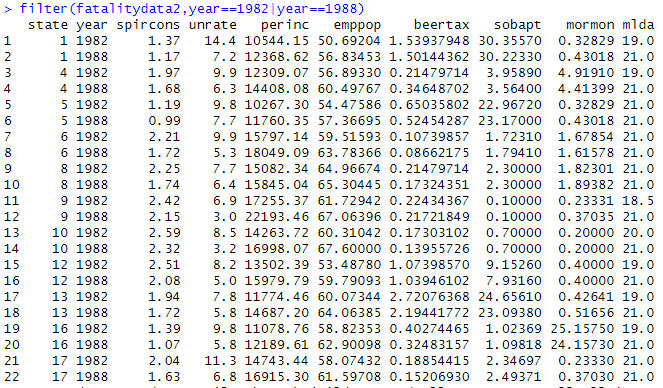
- 1982년과 1988년의 데이터를 사용하여 이 가설을 검증한다.

새로운 변수를 만드는 방법
- 샘플 내 교통사고로 인한 사망률 : Vehicle Fatality Rate (VFR)이 mrall로 표시되어 있다.
→ 값이 작아서 인구 1만 명당으로 한다.
→ fatalitydata2 <- mutate ( fatalitydata , fatality = fatalitydata$mrall * 10000 ) - mutate는 tidyverse package에서 새로운 변수를 만드는 함수입니다.
- 새로운 변수를 포함한 데이터가 생성된다.

샘플을 부분적으로 꺼내는 방법
- 여기서 샘플 중 1982년 데이터만 사용하고 싶다고 가정해보자.
- 이 경우 두 가지 방법이 있다.
(1) 패키지를 필요로 하지 않는 방법:
subset ( fatalitydata2, year == 1982 )
(2) tidyverse를 전제로 하는 방법:
filter ( fatalitydata2, year == 1982 )

- 1982년과 1988년 2년간의 데이터를 추출하고 싶은 경우
filter ( fatality , year == 1982 | year == 1988 )
| = or
※ subset에서도 동일

교통사고 사망과 알콜세: 1982년
- 맥주에 대한 세금의 계수는 부호가 양수이고 유의미하지 않다.
fatality : 사망률
beertax : 세율





교통사고 사망과 알코올 세금: 1985년

교통사고 사망과 알코올 세금: 무엇이 문제인가?
- 이 추정식에는 교통사고로 인한 사망률에 영향을 미칠 수 있는 변수(통제변수)가 다수 누락되어 있다.
→ 누락변수 편향의 문제 - 구체적으로는 도로의 질, 도시냐 농촌이냐, 교통량, 사회의 음주운전에 대한 태도(문화적 요인) 등
→ 이러한 요인들이 알코올에 대한 세율에 영향을 미치면 점점 더 편향성이 커진다. - "필요한 통제변수를 모두 설명변수로 도입"하면 문제가 해결되나 현실적으로 불가능
- 각 주별 사망률의 이질성을 고정효과로 통제한다.

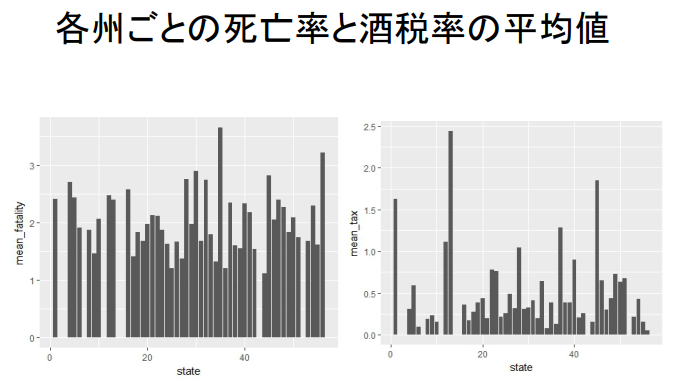
각 주별 사망률과 세율의 평균값(표본 기간 동안의 평균값)
mean_fatal <- fatalitydata2 %>%
group_by ( state ) %>%
summarize (
mean_fatality = mean ( fatality , na.rm = TRUE )
)

각 주별 사망률과 주세율의 평균치입니다.
Panel 분석에 필요한 설정
- 패널 분석을 할 때, 어떤 변수명으로 표본을 식별하고 있는지,
더 나아가 어떤 변수명으로 시간을 식별하고 있는지를 명확히 할 필요가 있다. - 예를 들어, 재무 데이터를 이용한 분석의 경우
1) 증권코드 등으로 표본을 식별한다.
2) 연도(2021년 등)로 시간을 식별한다.

Panel 분석에 필요한 설정
- R에서 사용하는 데이터를 패널 데이터로 인식하도록 하기 위해 회귀식 코드에 다음과 같이 입력합니다.
index = c ( " state " , " year " )
이 경우 state는 표본의 ID를, year는 시점을 인식하는 변수이다.
- 패널 분석의 코드 예시는 다음과 같다.
panel_result1 = plm ( fatality(y) ~ beertax(x) , y,x는 참고
data = fatalitydata2 ,
index = c ( " state " , " year " ) ,
model = " pooling " )
pooling = OLS

고정효과 모델 추정
- 고정효과 모형은 다음과 같이 추정할 수 있다.
- 패널추정의 경우, 사용하는 함수는 lm이 아닌 plm
panel_result2 = plm ( fatality ~ beertax ,
data = fatalitydata2 ,
index = c ( " state " , " year " ) ,
model = " within " )
고정효과 모형의 경우 model = " within "
변량효과 모형의 경우 model = " random "
일반 OLS의 경우, model = " pooling "

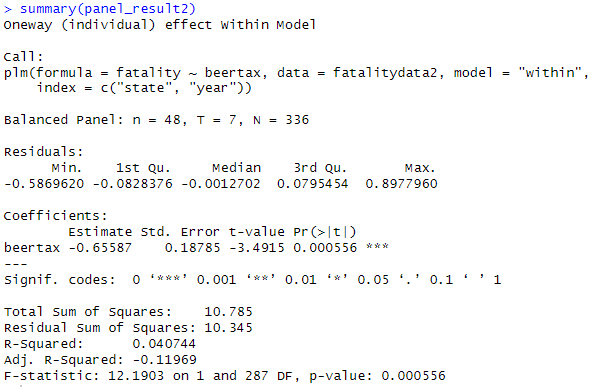
교통사고 사망과 알코올세: 7년간의 패널분석(고정효과모형)
맥주에 대한 세금의 계수는 부호가 마이너스이며 1% 수준에서 유의미함
→ 맥주 세율을 올리면 교통사고 감소
beertax -0.65587

고정효과 모델과 변량효과 모델
| (1) 고정효과모델 |
(2) 변량효과모델 |
|
| beertax | -0.656*** (0.188) |
-0.052 (0.124) |
| Constant | 2.067*** (0.100) |
|
| Observations | 336 | 336 |

고정효과 모델과 변량효과 모델
- Hausman 테스트는
# Hausman test of FE vs RE
phtest ( panel_result2 , panel_result2_ran )

p 값이 0 ⇒ 고정효과 모형이 지지된다.

교통사고 사망과 알코올세: 7년간의 패널분석(고정효과모형)
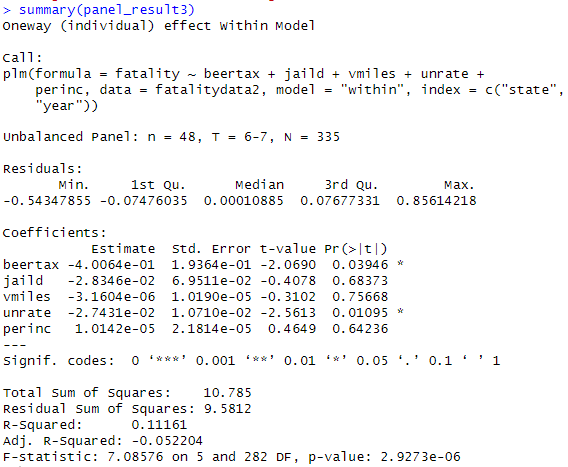
- 지금까지의 모델에 교통사고 사망에 영향을 미칠 수 있는 요인을 통제변수로 추가한다.
jaild : 사고를 내면 감옥에 가는지 여부의 더미(-)
vmiles : 운전자의 평균 주행거리(+)
unrate : 실업률(-)
perinc : 인구 1인당 소득(+)

교통사고 사망과 알코올세: 7년간의 패널분석(고정효과모형)




교통사고 사망과 알코올 세금: 시간 효과의 도입
- 연도 더미를 이용하여 시간효과 통제 : 어떤 해(1982년 등)에 1, 다른 해에 0을 부여하는 더미 변수
→ 특정 연도에 모든 경제주체에게 공통적으로 영향을 미치는 요인이 있을 경우, 이를 통제할 목적으로 도입
factor ( year )
→ 이것으로 연도 더미를 만들 수 있다.

교통사고 사망과 알코올 세금: 시간 효과의 도입
시간효과를 고려한 분석(OLS의 경우)은 다음과 같다: 결과는 동일하다.
panel_result4 = plm ( fatality ~ beertax + jaild + vmiles + unrate + perinc + factor ( year ) ,
data = fatalitydata2 ,
index = c ( " state " , " year " ) ,
model = " pooling " ) ← OLS
summary ( panel_result4 ) ← plm을 이용한 추정
panel_result5 = lm ( fatality ~ beertax + jaild + vmiles + unrate + perinc + factor ( year ) ,
data = fatalitydata2 )
summary ( panel_result5 ) ← lm을 이용한 추정

교통사고 사망과 알코올 세금: 시간 효과의 도입




교통사고 사망과 알코올 세금: 시간 효과의 도입





고정효과와 시간효과 모두 도입
- 1) 연도 더미 계수를 평가하지 않아도 되는 경우
panel_result6 = plm ( fatality ~ beertax + jaild + vmiles + unrate + perinc ,
data = fatalitydata2 ,
index = c ( " state " , " year " ) ,
model = " within " , ← 고정효과 모델
effect = " twoways " )
summary ( panel_result6 )
- 모델에 연도 더미를 추가하지 않는다.
effect = " twoways "
를 추가한다.

고정효과와 시간효과 모두 도입





고정효과와 시간효과 모두 도입
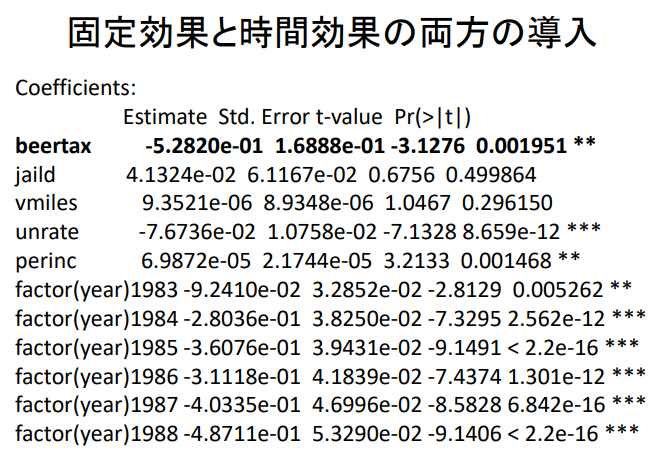
- 2) 연도 더미 계수를 평가하는 경우
panel_result7 = plm ( fatality ~ beertax + jaild + vmiles + unrate + perinc + factor(year) ,
data = fatalitydata2 ,
index = c ( " state " , " year " ) ,
model = " within " )
summary ( panel_result7 )
- 모델에 연도 더미 추가하기

고정효과와 시간효과 모두 도입

고정효과 모델의 특징
- 고정효과 모형은 시간에 따라 일정한 반면, 경제주체 간에는 변화하는 요인이 주는 편향성을 통제할 수 있다.
- 고정효과모형의 단점은 피설명변수(사망률)의 변화 요인 중
시간에 따라 변하지 않는 요인이 미치는 영향에 대해 검증할 수 없다는 점이다.

다음
- 인과관계를 추정하는 방법으로 차이의 차이 분석(Difference-in-Difference: DID)

'WBS - 2023 Fall > 기업경제학 연습' 카테고리의 다른 글
| (기업경제 #10) 성향 점수를 사용하지 않는 매칭 | 복원 매칭과 비복원 매칭 (0) | 2023.12.14 |
|---|---|
| (기업경제 #9) Matching (0) | 2023.12.06 |
| (기업경제 #8) 로지트 모델(Logit Model)과 프로빗 모델(Probit Model) (0) | 2023.11.29 |
| (기업경제 #7) DID | Difference-in-Difference (차이의 차이 분석) (0) | 2023.11.16 |
| (기업경제 #5) 더미 변수를 이용한 분석 (0) | 2023.11.02 |
| (기업경제 #4) 이상치 처리 | 선형 회귀 모델(2) (0) | 2023.10.26 |
| (기업경제 #3) 선형회귀 Model (0) | 2023.10.19 |
| (기업경제 #2) (0) | 2023.10.12 |



