기업경제학 실습: 제10회
蟻川靖浩

오늘의 일정
- 성향 점수를 사용하지 않는 매칭
- 복원 매칭과 비복원 매칭
참고 문헌:
- 커닝햄, S. 2021. 인과 관계 추론. 예일 대학 출판부.
- Ho,D., Imai,K., King,G., E. A. Stuart.2011. MatchIt: 파라메트릭 인과 추론을 위한 비모수적 전처리.
- 야스이 쇼타・주식회사 헉소엠『효과검증입문』기술평론사, 2020년
- 다카하시 마사무네, 『통계적 인과추론의 이론과 구현 잠재적 결과변수와 결측 데이터』공립출판사, 2022년
- 호시노 타다노, 다나카 히사미노 『R로 하는 실증분석』오름사, 2016년

매칭
- 다음 절차를 매칭(Matching)이라고 한다.
1) 처리군에 사용할 샘플을 선택한다. (분석 타겟)
2) 처리군에 포함된 샘플 하나하나에 대해 각각 공변량(통제에 사용하는 변수)이 일치하는 샘플을
대조군으로부터 선택하여 이를 반사실로 채택한다.
3) 공변량이 정확히 일치하는 샘플을 선택하지 못할 가능성

매칭
4) 공변량이 정확히 일치하는 표본을 찾을 수 없는 경우, 공변량이 '가장 가까운' 단위를 반사실로서 채택
5) 치료군과 대조군 사이에 매칭에 사용한 공변량에 대해 균형이 맞아야 한다.
6) 매칭된 각 조합마다 두 개의 차이를 취한다.
7) 각 조합의 차이의 평균을 취하면 '치료받은 사람 중 평균 치료효과
( Average Treatment Effect on the Treated, ATT ) '를 계산할 수 있다.

인과추론의 추정 대상(estimand)
- 통계적 인과 추론의 추정 대상(estimand)은 크게 평균 치료 효과(ATE)와
치료를 받은 사람 중 평균 치료 효과(ATT) 의 두 가지가 있다.
An estimand is a quantity that is to be estimated in a statistical analysis.
𝜏ₐₜₑ = 𝐸 [ 𝑌₁ᵢ 𝐷ᵢ = 1 ] - 𝐸 [ 𝑌₀ᵢ 𝐷ᵢ = 0 ]
𝜏ₐₜₜ = 𝐸 [ 𝑌₁ᵢ 𝐷ᵢ = 1 ] - 𝐸 [ 𝑌₀ᵢ 𝐷ᵢ = 1 ] - 매칭에서 추정 대상은 ATT : 치료군 표본에 대해 대조군에서 매칭 상대를 선택하기 때문에
매칭 후의 데이터는 치료군 표본을 기준으로 구성되어 있다. - 어떤 정책을 취했을 때 그 정책의 대상에게 어느 정도 영향을 미쳤는지를 보는 경우 ATT를 사용하는 경우가 많다.
𝐷ᵢ = 1 : 치료를 받음
𝐷ᵢ = 0 : 치료를 받지 않음


매칭을 이용한 분석 사례: 자본 구성의 문제
- 무차입기업은 이자부채가 있는 기업과 비교했을 때 어떤 특징을 가지고 있을까?
- 처리군 : 이자부채가 0인 기업
- 대조군 : 이자부채가 플러스인 기업
- 두 그룹을 비교하기 위해 어떤 기업을 대조군으로 선택해야 하는가?
Agrawal, A. and Nagarajan,N.J. 1990. 기업 자본 구조, 대리인 비용, 소유권 통제: 전액출자기업의 사례, 금융학회지 45: 1325-1331.

샘플 선택
- 표본 기간 : 1979년 - 1983년
- 처리군인 무이자 부채 제로 기업 : 5년간 장기부채가 제로인 기업
→ 표본 수는 104개 - 대조군 선정 방법: 이자부채가 0인 기업 1곳에 대해 최소 1곳의 대조군 기업을 찾아야 한다.
→ 기준은?

샘플 선택
- 대조군 선정 기준
1) 이자부채가 플러스인 기업을 찾는다.
2) 처리군 기업과 동일한 업종 코드
3) 총자산 규모가 비슷함
※ 이자부채 플러스 기업의 정의: 기업가치(시가총액+부채 장부가액) 대비 장기부채의 비율이
1979년부터 1983년 동안 지속적으로 5% 이상을 유지한 기업 - 82개 기업이 대조군으로 남는다.

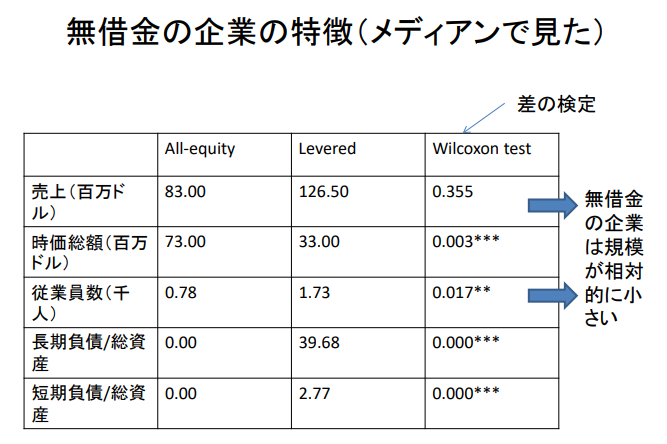
무차입 기업의 특징(미디어에서 본)
| All-equity (무차입) |
Levered (차입) |
Wilcoxon test (차이 검증) |
||
| 매출($ mil.) | 83.00 | 126.50 | 0.355 → | 무차입 기업은 상대적으로 규모가 작다. |
| 시가총액($ mil.) | 73.00 | 33.00 | 0.003*** | |
| 종업원수(천명) | 0.78 | 1.73 | 0.017** → | |
| 장기부채/총자산 | 0.00 | 39.68 | 0.000*** | |
| 단기부채/총자산 | 0.00 | 2.77 | 0.000*** |
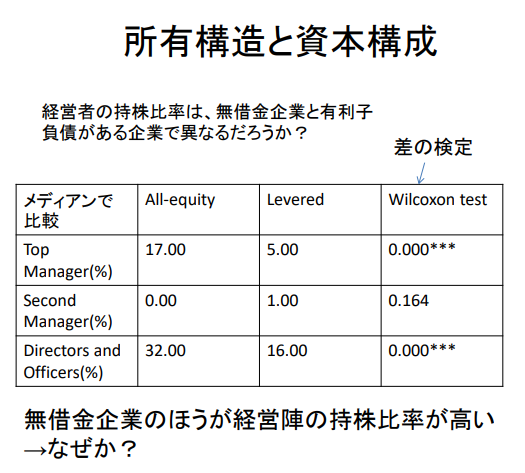
소유구조와 자본구조
무차입 기업과 유이자 부채가 있는 기업에서 경영자의 지분율이 다를까?
| Median 비교 | All-equity | Levered | Wilcoxon test (차이 검증) |
| Top Manager(%) | 17.00 | 5.00 | 0.000*** |
| Second Manager(%) | 0.00 | 1.00 | 0.164 |
| Directors and Officers(%) | 32.00 | 16.00 | 0.000*** |
무차입 기업에서 경영진의 지분율이 더 높다.
→ 왜?
지분율 비교
- 경영진(이사+집행임원)의 주식보유 비율 비교
- 처리군 : 무이자 부채 기업이자 경영진이 친인척인 경우
- All-equity : 48.00%
- Levered : 20.00%.
- 처리군 : 무이자 부채 기업이자 경영진이 서로 친족이 아닌 경우
- All-equity : 21.00%
- Levered : 12.00%
- 처리군 : 무이자 부채 기업이자 경영진이 친인척인 경우

자본 구성의 문제: 결론
- 무차입 기업의 특징은 통제군 기업과 비교했을 때
1) 경영진의 지분율이 높다.
2) 동족기업(family firm)인 경향이 강하다.
→ 동족기업이 '파산비용'이 더 크기 때문에 부채를 회피하는 경향 - 일본에서도 비슷한 경향이 관찰됨
Saito, T. 2008. 가족 기업과 기업 성과: 일본에서의 증거, 일본 국제 경제 저널 22, 620-646.

R을 이용한 성향 점수를 사용하지 않는 매칭
- 예시 : 한 기업에서 직원들의 역량 향상을 위한 교육 프로그램 실시
- 교육 참여는 임의적이다.
- 교육 참여가 임금에 미치는 인과관계를 알고 싶다.


R을 이용한 성향점수를 사용하지 않는 매칭
- 데이터는
data_wage <- read.csv ( " wage_training.csv " , header = TRUE )
wagea : 교육 참여 후 임금(만엔)
T : 교육 참여 여부 ( 참여 = 1 , 불참 = 0 )
years : 경력연수
wageb : 연수 전 임금(만엔)

R을 이용한 경향점수를 사용하지 않는 매칭
- 각 데이터 항목에 이름 붙이기
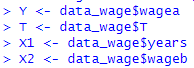
Y <- data_wage $ wagea # 연수기간 후 임금
T <- data_wage $ T # 교육훈련 참여 여부
X1 <- data_wage $ years # 경력연수
X2 <- data_wage $ wageb # 연수 이전 임금

R을 이용한 경향성 점수를 사용하지 않는 매칭
- 매칭을 하기 전에 치료군과 대조군의 단순 평균 임금 비교를 위해 다음과 같이 계산한다.
{ sum ( T * Y ) / sum ( T ) } - { sum ( ( 1 - T ) * Y / sum ( 1 - T ) ) }
sum ( T ) : T = 1 의 수
sum ( 1 - T ) : T = 0 의 수
sum ( T * Y ) : T = 1 의 임금의 합계
[1] -1.128488

평균 임금의 차이는 -1.13만엔
→ 교육과 임금의 차이는 음의 상관관계
→ 만약 훈련 참여와 잠재적 임금이 완전히 무작위로 결정된다면, 이 차이는 인과효과로 이해할 수 있다.

R을 이용한 경향점수를 사용하지 않는 매칭
- 연수 참여와 경력기간, 연수 전 임금의 상관관계 계수 계산
cor ( T , X1 )
[1] -0.1908208
cor ( T , X2 )
[1] -0.1839177

- 상관계수는 음수
→ 경력이 짧고 임금이 낮은 직원일수록 더 적극적으로 교육에 참여한다.
→ '교육 참여와 잠재적 임금이 완전히 무작위적'이라는 가정은 성립하지 않는다. - 인과적 효과로 볼 수 없으므로 매칭을 수행한다.
- 여기서는 '경력년수', '교육훈련 이전 임금' 두 가지 임금으로 매칭

R을 이용한 경향성 점수를 사용하지 않는 매칭
- 매칭의 구체적인 방법 : Matching 패키지 사용
library ( Matching )
- Match라는 함수를 이용하여 최근접 매칭에 의한 '치료군의 평균 치료 효과(ATT)'를 추정할 수 있습니다.

R을 이용한 경향성 점수를 사용하지 않는 매칭
- Match 함수
Match ( 성과 변수 , 치료 변수 , 매칭에 사용할 공변량 , 거리 척도 선택 )
(1) 치료 변수: 치료를 받고 있는 경우 1, 그렇지 않은 경우 0을 취하는 2값 치료 변수를 지정 ( T = 1 or 0 )
(2) 매칭에 사용할 공변량: 여러 개일 경우, cbind ( X1 , X2 , ... ) 로 변수를 묶는다.
NN.Euclid <- Match ( Y , T , cbind ( X1 , X2 ) , Weight = 1 )

R을 이용한 경향점수를 사용하지 않는 매칭
(3) 거리 척도 선택 : X₁, X₂의 값이 가장 가까운 샘플끼리 매칭하는 방법
= '최근접 매칭(nearest-neighbor matching)'이라고 한다.
- 최근접 매칭을 하기 위해서는 샘플 간의 '근접성'을 정의할 필요가 있다.
- 여기서 X₁ 은 경험연수, X₂ 는 연수 이전 임금

R을 이용한 성향 점수를 사용하지 않는 매칭
- 샘플 간의 근접성을 측정하는 방법으로 대표적인 방법은 다음 두 가지가 있습니다.
1 : 표준화 유클리드 거리 d ( i , j ) = √ ∆²₁ᵢⱼ + ∆²₂ᵢⱼ
2 : 마하라노비스 거리 d ( i , j ) = √ { 1 / ( 1 - ρ² ) } [ ∆²₁ᵢⱼ + ∆²₂ᵢⱼ - 2 ρ ∆²₁ᵢⱼ ∆²₂ᵢⱼ ]
∆₁ᵢⱼ = ( X₁ᵢ - X₁ⱼ ) / σ₁ , ∆₂ᵢⱼ = X₂ᵢ - X₂ⱼ / σ₂
※ σ₁과 σ₂는 X₁과 X₂의 표준편차, ρ는 X₁과 X₂의 상관관계 계수

R을 이용한 성향 점수를 사용하지 않는 매칭
(3) 거리 척도 선택 :
- 표준화 유클리드 거리를 사용하는 경우 ' weight = 1 '
- 마하라노비스 거리를 사용하는 경우 ' weight = 2 '

R을 이용한 경향성 점수를 사용하지 않는 매칭
(4) ATT 추정
- 교육 참여 : 치료군, 교육 불참 : 대조군
- 대조군 중 거리 d ( i , j ) 의 값이 j 중 가장 작은 샘플을 샘플 i 의 매칭 상대로 선택
- 처리군과 대조군의 성과변수(교육기간 후 임금)의 차이를 각 조합별로 계산하여 그 평균을 구한다.

R을 이용한 경향성 점수를 사용하지 않는 매칭
- Match 함수
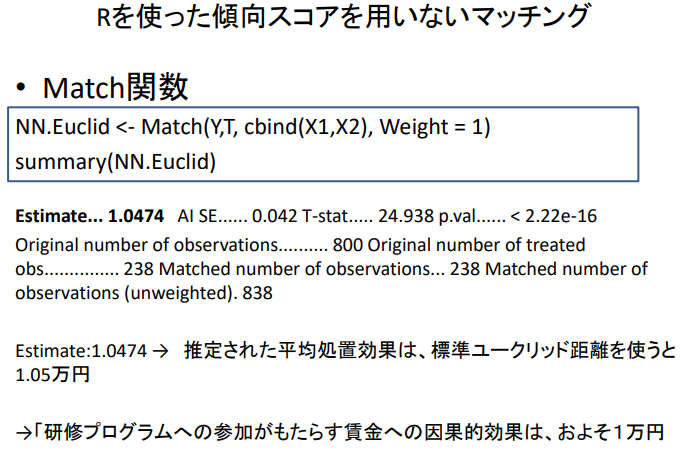
NN.Euclid <- Match ( Y , T , cbind ( X1 , X2 ) , Weight = 1 )
summary ( NN.Euclid )
T = 1 or 0
Estimate ... 1.0474
AI SE........... 0.042
T-stat........... 24.938
p.val............. < 2.22e-16
원래 관측 횟수............................... 800
처리된 관측의 원래 수.................... 238
일치하는 관측 수............................ 238
일치하는 관측치 수(가중치 없음)... 838
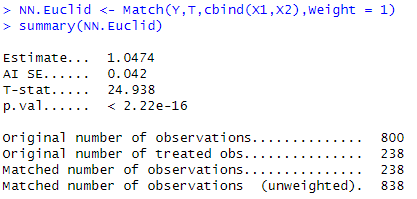
Estimate : 1.0474 → 추정된 평균 처리 효과는 표준 유클리드 거리를 사용하면 1.05만 엔
→ 연수 프로그램 참여가 가져오는 임금에 대한 인과적 효과는 대략 1만 엔이다.

R을 이용한 성향 점수를 사용하지 않는 매칭
- Match 함수
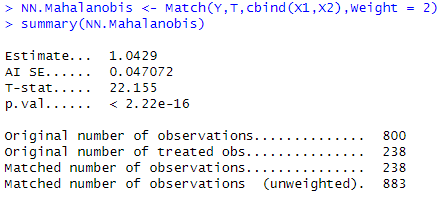
NN.Mahalanobis <- Match ( Y , T , cbind ( X1 , X2 ) , Weight = 2 )
summary ( NN.Mahalanobis )
- Estimate... 1.0429
AI SE......... 0.047072
T-stat......... 22.155
p.val........... < 2.22e-16
→ 추정된 평균 처리효과는 1.05만 엔
→ "연수 프로그램 참여가 임금에 미치는 인과적 효과는 대략 1만 엔이다.

성향 점수 매칭(Propensity Score Matching)
- 여러 공변량에서 '성향 점수(propensity score)'를 생성하고, 그 값을 이용하여 매칭을 수행한다.
→ 성향 점수는 하나의 수치이므로 여러 공변량을 사용하여 매칭하는 것보다 간편함 - 성향 점수를 계산하는 데 있어 로짓/프로빗 모델을 이용한다.
- 성향점수 매칭으로 매칭 샘플을 생성, 이를 이용하여 회귀분석 등 수행

성향 점수 매칭
- '개입'을 받은 그룹 = 치료군
- '개입'을 받지 않은 그룹 = 대조군
- 치료군과 비슷한 성향점수를 가진 표본을 대조군에서 찾아 짝을 짓는다.
- 성향점수란 '치료군에 들어갈 확률' 혹은 '개입'이 이루어질 확률을 의미한다.

R을 이용한 성향 점수 매칭
- MatchIt 패키지를 사용하여 경향성 점수 매칭을 수행하는 방법을 소개합니다.
library ( MatchIt )
- 특히 '최근접 매칭'을 통해 '치료받은 사람 중 평균 치료효과(Average Treatment Effect on the Treated, ATT)' 를 추정하는 방법을 소개합니다.

R을 이용한 경향성 점수 매칭
- 데이터는
data ( lalonde )
- 이는 Dehejia and Wahba (1999)에서 사용된 직업훈련과 이후 임금의 관계를
성향 점수 매칭을 검증하기 위한 데이터입니다.
데헤지아, 라지브, 사덱 와바. 1999. 비실험적 연구의 인과적 효과: 교육 평가에 대한 재평가 프로그램.
미국 통계 협회 저널 94 (448): 1053-1062.

Dehejia and Wahba (1999)
- 각 데이터 항목은
표본 수는 445개, 변수는 12개이다.
age : 나이
educ : 교육연수
race : 인종
nodegree : 샘플의 고졸 여부
married : 샘플이 기혼자

Dehejia and Wahba (1999)
- 각 데이터 항목은
re74: 1974년 실질소득
re75: 1975년 실질소득
re78: 1978년 실질소득
u74: 1974년 실질소득이면 1, 그렇지 않으면 0을 부여하는 더미변수
u75: 1975년 실질소득이면 1, 그렇지 않으면 0을 부여하는 더미변수
treat: 치료군이면 1을 부여하는 더미변수
→ 교육훈련을 받고 있는 표본이 처리군 ( 1 or 0 )

최근접 매칭
- 성향 점수의 차이가 가장 작은 샘플끼리 매칭하는 방법은
'최근접 매칭 ( Nearest-Neighbor Matching ) ' - 차이가 0인 경우에만 일치하는 것은 ' Exact Matching '

최근점 매칭
Nearest Neighbor Matching
m.out_1 <- matchit ( treat ~ re74 + re75 + educ + race + age + nodegree + married ,
data = lalonde ,
method = " nearest " )


일치하는 샘플을 꺼내기
일치하는 샘플을 추출하려면
m.data_1 <- match.data ( m.out_1 )
match.data 함수를 사용하면 된다

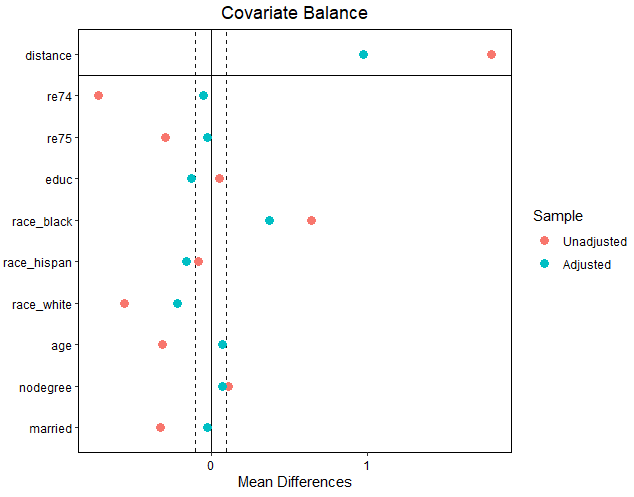
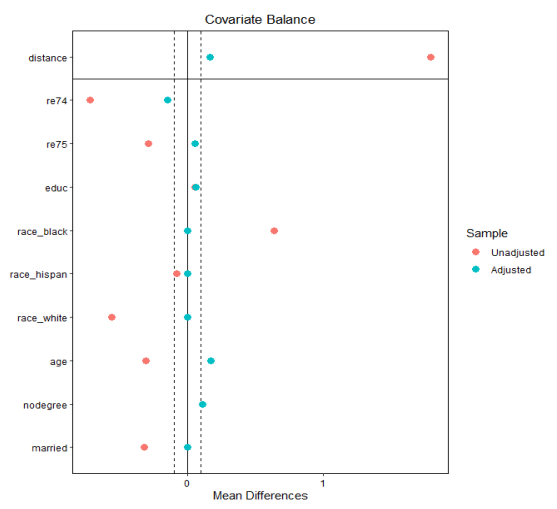
공변량 균형 시각화
# install.packages ( " cobalt " )
library ( cobalt )
love.plot ( m.out_1 , threshold = .1 )


Covariate Balance
가로축은 표준화 평균차(Average Standardized Absolute Mean Distance:ASAM)
평균의 차이를 그 표준오차로 나눈 것
매칭 전 샘플을 사용하여 회귀분석을 수행합니다.
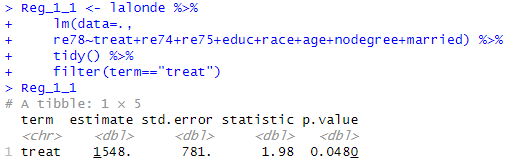
Reg_1_1 <- lalonde % > %
lm ( data =. ,
re78 ~ treat + re74 + re75 + educ + race + age + nodegr + married ) % > %
tidy ( ) % > %
filter ( term == " treat " )
Reg_1_1

매칭 후 샘플을 사용하여 회귀분석을 수행합니다.
- 이미 매칭이 끝났기 때문에 통제변수는 필요 없다.
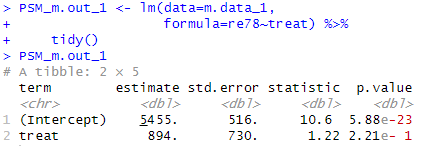
PSM_m.out_1 <- lm ( data = m.data_1 ,
formula = re78 ~ treat ) % > %
tidy ( )
PSM_m.out_1

두 결과를 비교하면
- 매칭 전:
term estimate std.error statistic p.value
treat 1548. 781. 1.98 0.0480 - 매칭 후:
term estimate std.error statistic p.value
treat 894. 730. 1.22 2.21e- 1

매칭에 사용된 성향 점수 도출
- 성향 점수를 보고 싶다면 먼저 로짓 모델(또는 프로빗)을 추정한다.
Logit_m.out_1 <- glm ( treat ~ re74 + re75 + educ + race + age + nodegree + married ,
family = binomial ,
data = lalonde )
treat ( Y ) = 1 or 0

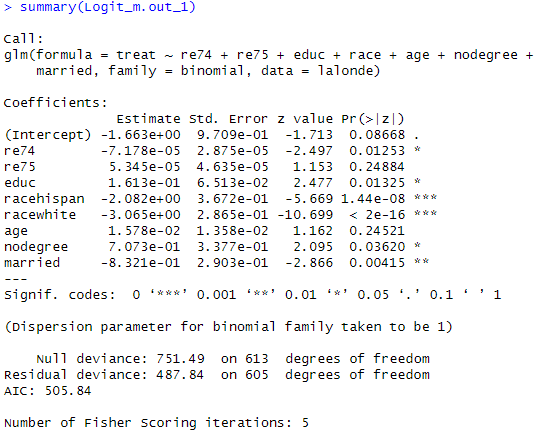
summary ( Logit _m.out_1 )
로지트 모델 추정 결과


매칭에 사용된 성향 점수 도출
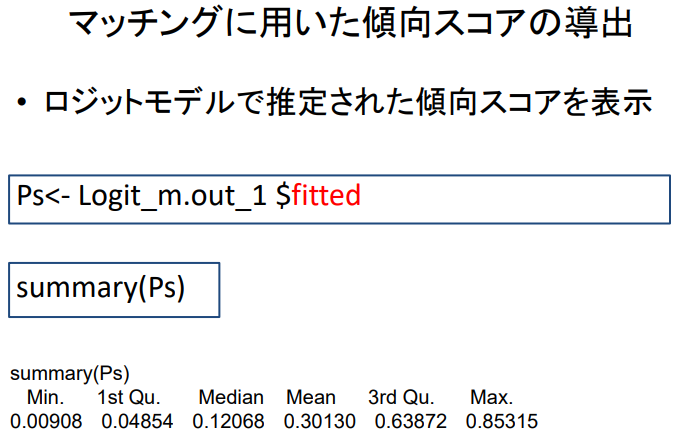
- 로지트 모형으로 추정된 성향 점수를 표시합니다. (직업훈련을 받을 확률, 예측 모델)
Ps <- Logit_m.out_1 $fitted
summary ( Ps )
summary(Ps)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00908 0.04854 0.12068 0.30130 0.63872 0.85315
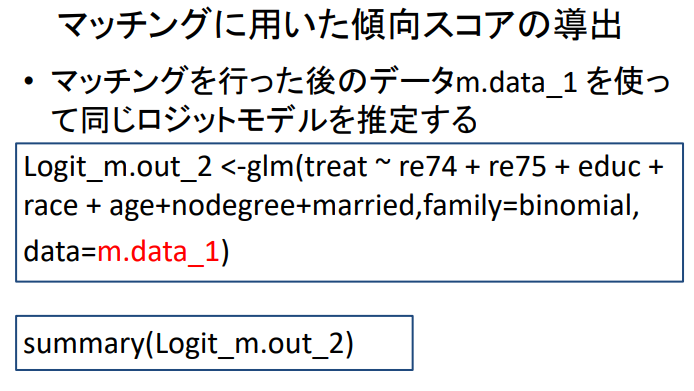
매칭에 사용된 경향성 점수 도출
- 매칭을 수행한 후의 데이터 m.data_1을 사용하여 동일한 로짓 모델을 추정한다.
Logit_m.out_2 <- glm ( treat ~ re74 + re75 + educ + race + age + nodegree + married ,
family = binomial ,
data = m.data_1 )
treat = y = 1 or 0
summary ( Logit_m.out_2 )
로지트 모델 추정 결과
유의미한 계수 수 감소
***이 있는게 매칭이 안됐다는 것, ***가 없어지면 매칭이 됐다는 뜻
***는 두개의 차이가 있다는 뜻

최근접 매칭
- '최근접 매칭'의 경우, 두 샘플 간의 거리에 제한이 없다.
- 그래서 추가 조건으로 거리가 일정 범위 내에 있어야 한다는 것을 요구한다.
- 이 ε ( 범위 ) 를 caliper라고 한다.

최근접 매칭
- Caliper 설정 예시: caliper =.25
- 성향점수(PS)에 대해 완전히 일치하거나 0.25 표준편차 이내로 일치할 수 있다.
- 샘플이 없는 경우, 대조군 샘플에서 떨어뜨림

최근접 매칭
- 두 샘플 사이의 거리에 일정한 제한을 추가합니다.
→ caliper = 0.25의 조건에서 최근접 매칭을 수행한다.
m.out_2 <- matchit ( treat ~ re74 + re75 + educ + race + age + nodegr + married ,
data = lalonde ,
method = " nearest " ,
caliper = 0.25 )

두 결과를 비교하면
- 매칭 전:
term estimate std.error statistic p.value
treat 1548. 781. 1.98 0.0480 - 매칭 후:
term estimate std.error statistic p.value
treat 2029. 945. 2.15 3.28e- 2

최근접 매칭을 수행한다.
- 두 샘플 사이의 거리에 일정한 제한을 추가합니다.
→ caliper = 0.25 및 exact = " married " 조건에서 최근접 매칭을 수행한다.
m.out_3 <- matchit ( treat ~ re74 + re75 + educ + race + age + nodegree + married ,
data = lalonde ,
method = " nearest " ,
caliper = 0.25 ,
exact = " married " )

두 결과를 비교하면
- 매칭 전:
term estimate std.error statistic p.value
treat 1548. 781. 1.98 0.0480 - 매칭 후:
term estimate std.error statistic p.value
treat 2238. 983. 2.28 2.38e- 2

Covariate Balance
복원 매칭에 대한 고찰
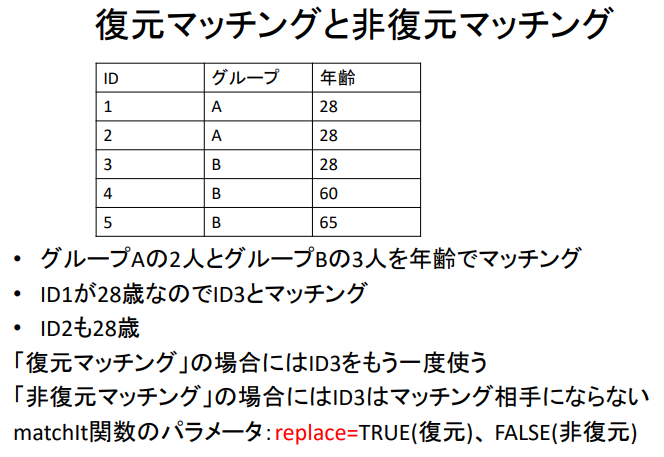
- 복원 매칭은 한 번 매칭 쌍에 사용된 샘플을 다시 대조군으로 되돌리는 방법입니다.

복원 매칭과 비복원 매칭
| ID | Group | 연령 |
| 1 | A | 28 |
| 2 | A | 28 |
| 3 | B | 28 |
| 4 | B | 60 |
| 5 | B | 65 |
- 그룹 A의 2명과 그룹 B의 3명을 연령으로 매칭
- ID1이 28세이므로 ID3과 매칭
- ID2도 28세
'복원 매칭'의 경우에는 ID3를 다시 한번 사용
'비복원 매칭'의 경우 ID3는 매칭 대상이 아님
matchIt 함수의 파라미터 : replace = TRUE ( 복원 ) , FALSE ( 비복원 )
최근접 매칭하기
- 비복원에 의한 매칭
m.out_1_no_replace <- matchit ( treat ~ re74 + re75 + educ + race + age + nodegree + married ,
data = lalonde ,
replace = FALSE ,
distance = " glm " ,
method = " nearest " )
- 복원을 통한 매칭
m.out_1_replace <- matchit ( treat ~ re74 + re75 + educ + race + age + nodegree + married ,
data = lalonde,
replace = TRUE ,
distance = " glm " ,
method = " nearest " )
distance = " glm " : 기본 설정("distance="glm"을 생략한 경우와 동일)으로 로짓 모델을 사용하여 성향 점수를 계산

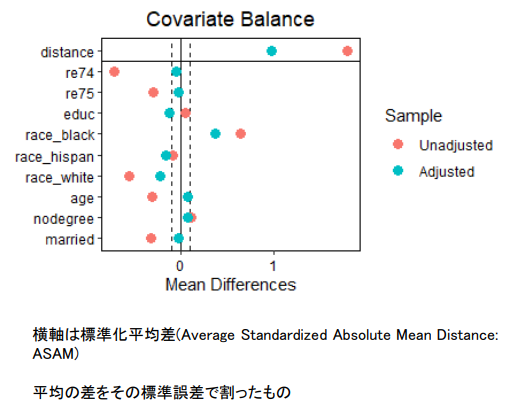
공변량 균형 시각화
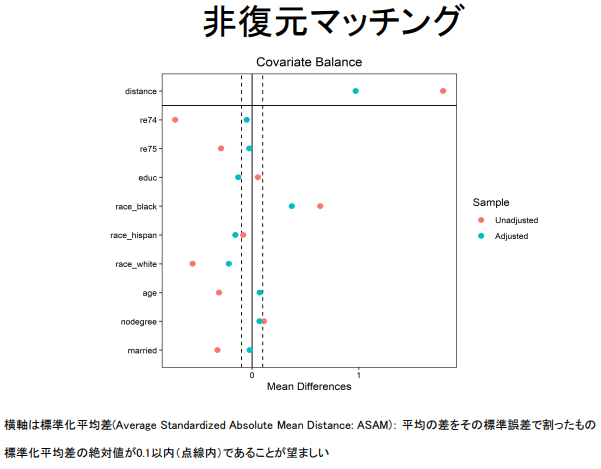
비복원
love.plot ( m.out_1_no_replace , threshold = .1 )
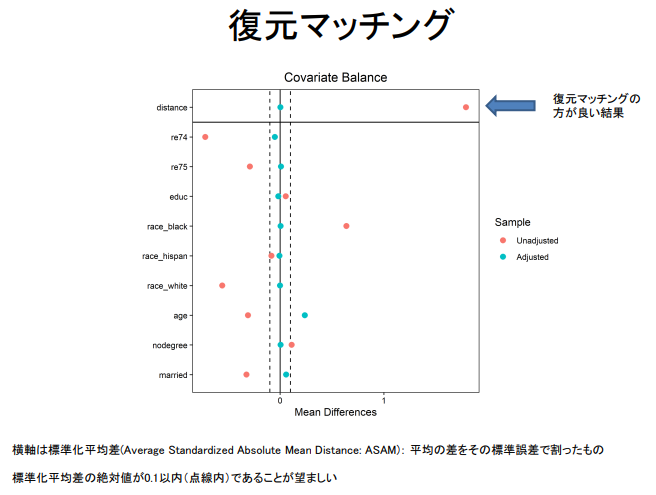
복원
love.plot ( m.out_1_replace , threshold = .1 )

비복원 매칭
가로축은 표준화 평균차(Average Standardized Absolute Mean Distance: ASAM) : 평균의 차이를 그 표준오차로 나눈 것
표준화 평균차이의 절대값이 0.1 이내(점선 내)인 것이 바람직하다.
복원 매칭
복원 매칭이 더 나은 결과
복원 매칭과 비복원 매칭
각 수치는 개체 간 거리
| 대조군 | ||||
| ID4 | ID5 | ID6 | ||
| 치료군 | ID1 | 0.4 | 0.1 | 10.0 |
| ID2 | 100.0 | 0.2 | 4.0 | |
| ID3 | 5.0 | 3.0 | 0.3 | |
- 최근접 매칭(탐욕 매칭, greedy matching)은 개별 거리의 최소화를 목표로 하기 때문에
비복원의 경우, 부적절한 매칭이 이루어질 위험이 있다. - ID1과 ID5 사이의 거리가 최소(0.1)이므로 양자가 매칭된다.
→ 다음은 ID2와 ID5의 조합인데 이는 비복원의 경우 사용할 수 없다.
→ ID4와 ID6의 조합이 다음으로 거리가 짧다(0.3).
→ 반드시 매칭 상대를 찾는다면, ID2는 ID4와 매칭이 된다.

복원 매칭과 비복원 매칭
- 복원을 통한 매칭은 데이터에 포함된 정보가 낭비되지 않는다는 장점이 있다.
- 반면 복원의 경우 동일한 샘플이 여러 번 등장하기 때문에 매칭된 대조군 샘플의 데이터 독립성이 떨어진다.
→ 이 점을 조정하기 위해 매칭의 '가중치', 즉 같은 샘플이 몇 번이나 사용되었는지를 추정할 때 고려해야 하며, 이후 분석이 복잡해진다. - Caliper를 사용하여 거리를 일정 범위로 제한하면서 비복원 매칭을 사용하는 경우도 많다.
- 비복원과 복원은 장단점이 있다.

복원 추출을 통한 경향성 점수 매칭
- 1단계 : 복원 매칭
m.out_1_replace <- matchit ( treat ~ re74 + re75 + educ + race + age + nodegree + married ,
data = lalonde ,
replace = TRUE ,
distance = " glm " ,
method = " nearest " )
- 2단계: 치료군 및 일치하는 대조군만 추출한다.
m.data_1_replace <- match.data ( m.out_1_replace )

복원 추출을 통한 경향성 점수 매칭
- 3단계: 성향 점수 매칭 후 데이터를 이용한 회귀분석, 치료 효과 평가
- 앞서 언급했듯이, 복원 매칭에서는 동일한 샘플이 여러 번 등장하기 때문에
매칭된 대조군 샘플의 데이터 독립성을 잃게 되므로 회귀분석에서도 이 점을 조정해야 한다.
→ 가중최소제곱법(WLS: Weighted Least Squares)을 이용하여
매칭의 가중치로 인한 오차항의 불균등 분산 문제를 수정한다.

복원 추출을 통한 경향성 점수 매칭
- 3단계 : 성향 점수 매칭 후 데이터를 이용하여 회귀분석, 치료 효과 평가
PSM_m.out_replace_1 <- lm ( data = m.data_1_replace ,
formula = re78 ~ treat ,
weights = weights )
weights = : WLS를 이용하여 오차항을 수정하도록 지시
= weights : '매칭의 가중치'를 조정하기 위해 매칭에서 얻은 파라미터 weights를 사용한다. (우연히 파라미터 명이 같음)
※ weights는 복원 매칭에서 동일한 샘플이 사용된 빈도에 관한 값

복원 추출을 통한 경향성 점수 매칭
- 4단계: 성향점수로 매칭을 수행해도 여전히 공변량의 균형이 맞지 않을 가능성이 있으므로
회귀분석 모델에 공변량을 포함한다.
PSM_m.out_replace_2 <- lm ( data = m.data_1_replace ,
formula = re78 ~ treat + re74 + re75 + educ + race + age + nodegree + married ,
weights = weights )

비복원 + Caliper + 설명변수에 공변량을 추가한 경우
- 비복원 매칭에 Capliper를 추가한 경우
매칭
m.out_caliper <- matchit ( treat ~ re74 + re75 + educ + race + age + nodegree + married ,
data = lalonde ,
method = " nearest " ,
caliper = 0.25 )
- 일반 OLS를 사용하는
OLS
PSM_m.out_caliper <- lm ( data = m.data_caliper ,
formula = re78 ~ treat + re74 + re75 + educ + race + age + nodegree + married )
treat = 1 or 0

비복원 매칭 + Caliper

복원 추출을 통한 경향성 점수 매칭
- 치료 효과의 계수( treat 의 계수 )
모델 1 : 복원 없음 : 894
모델 2 : 복원 없음 + 설명변수에 공변량 포함 : 1,345
모델 3 : 복원 있음 : 1,992
모델 4 : 복원 있음 + 설명변수에 공변량 포함 : 1,926
모델 5 : 복원 없음 + Caliper + 설명변수에 공변량 : 1,887
| 복원 | Caliper | 공변량 | 계수 | |
| 모델1 | X | X | X | 894 |
| 모델2 | X | X | O | 1,345 |
| 모델3 | O | X | X | 1,992 |
| 모델4 | O | X | O | 1,926 |
| 모델5 | X | O | O | 1,887 |

다음회
- 불연속회귀

'WBS - 2023 Fall > 기업경제학 연습' 카테고리의 다른 글
| (기업경제 #11) 불연속 회귀의 개념 (0) | 2023.12.21 |
|---|---|
| (기업경제 #9) Matching (0) | 2023.12.06 |
| (기업경제 #8) 로지트 모델(Logit Model)과 프로빗 모델(Probit Model) (0) | 2023.11.29 |
| (기업경제 #7) DID | Difference-in-Difference (차이의 차이 분석) (0) | 2023.11.16 |
| (기업경제 #6) 패널 분석 (Panel data analysis) (0) | 2023.11.09 |
| (기업경제 #5) 더미 변수를 이용한 분석 (0) | 2023.11.02 |
| (기업경제 #4) 이상치 처리 | 선형 회귀 모델(2) (0) | 2023.10.26 |
| (기업경제 #3) 선형회귀 Model (0) | 2023.10.19 |



