기업경제학 실습: 제11회
蟻川靖浩

참고 문헌
- 야스이 쇼타, 『효과 검증 입문』기술평론사, 2019년
- Angrist, J. D., and J. Pischke. 2009. 대부분 무해한 계량경제학. 프린스턴 대학 출판부.
- Angrist, J. D., and J. Pischke. 2015. 메트릭 마스터하기: 원인에서 결과로 가는 길. 프린스턴 대학 출판부.
- Boone, A. L. and J.T. White. 2015.
기관 소유가 기업의 투명성과 정보 생산에 미치는 영향. 금융 경제학 저널, 117:508-533. - Cunningham, S. 2021. 인과적 추론. 예일 대학 출판부.
- Imbens,G. and T.Lemieux.2008. 회귀 불연속성 설계: 실무 가이드. 계량경제학 저널 62: 615-635.

오늘의 일정
- 불연속 회귀의 개념

불연속 회귀(Regression Discontinuity Design:RDD)
- 임의의 규칙에 따른 변수의 불연속성을 이용하여 변수들 간의 인과관계를 분석하는 방법
- 임의의 기준에 의한 불연속성이 있는 경우, 그 불연속성 근처에 분포하는 표본은 '대략' 비슷하다고 가정할 수 있다.
- 이 기준의 양쪽에서 규칙의 적용 여부가 다르다면, 불연속점 근처에서 비교하면 해당 규칙의 효과를 측정할 수 있다.

RDD의 예
- 미국에서 술을 마실 수 있는 연령은 21세부터: MLDA(the Minimum Legal Drinking Age)
- 다음 페이지의 그림은 인구 10만 명당 연령별 사망률과 생일의 관계를 나타낸 것이다.
- 21세부터 생일 사망률이 불연속적으로 증가

생일과 사망률의 관계
생일부터 몇일인지
21세 생일

생일과 사망률의 관계
- MLDA(the Minimum Legal Drinking Age)와 사망률 사이에 인과관계가 있을까?
- 더미 변수 Dₐ 는
Dₐ = 1 : 연령이 21세 이상일 경우 → 치료군
Dₐ = 0 : 연령이 21세 미만인 경우 → 대조군

생일과 사망률의 관계
- 더미 변수 Dₐ는 샘플이 치료군에 들어가는지 여부를 나타내는 변수이다,
1) 치료군에 들어가는지 여부에 대한 불확실성이 없다.
→ 나이와 음주 가능 여부의 관계에는 불확실성이 없다.
2) 21세 시점에서 "불연속적"으로 표본이 대조군에서 처리군으로 진입: Sharp RDD라고 한다.

Sharp RDD
- 샘플이 처리군에 들어갈지 여부를 결정하는 변수를 강제변수(Forced Variable) (또는 실행변수(Running Variable)) 라고 한다.
- Sharp RDD에서는 강제변수가 경계선(Cut-Off Point)을 넘으면 샘플이 확실히 처리군으로 전환된다.
- 음주 가능 연령의 예에서 21세가 경계선이며, 불확실성은 없다.
- 경계선 결정은 샘플의 외생적 결정이다.

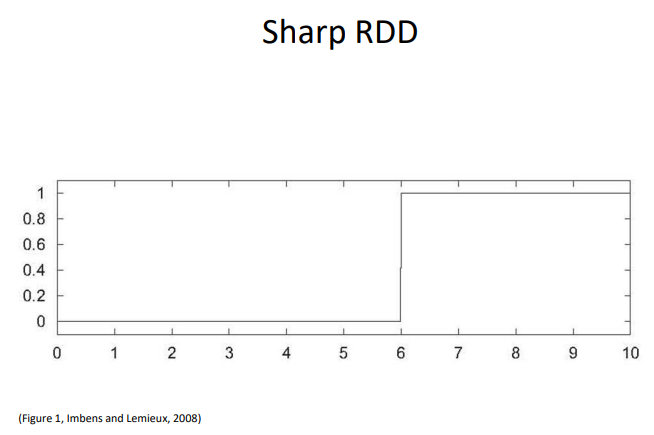
Sharp RDD
- 세로축은 치료군에 들어갈 확률
- 가로축은 강제 변수
- 경계선이 x = 6
- Sharp RDD의 경우, 강제변수가 6을 넘어서는 순간, 처리군에 들어갈 확률이 0에서 1로 상승한다.
→ 처리군에 들어갈 확률은 경계선에서 불연속적으로 변화

Sharp RDD
Sharp RDD의 중요한 가정
- 표본의 '국소적 연속성' : 경계선 부근에 위치한 표본은 비슷하다.
예: 20세와 22세의 표본은 술을 마실 수 있는지 여부를 제외하고는 차이가 없다. - 경계선 결정은 표본의 외생적 결정이다.
예: '21세'라는 규칙을 결정하는 데 당사자가 관여하지 않는다.

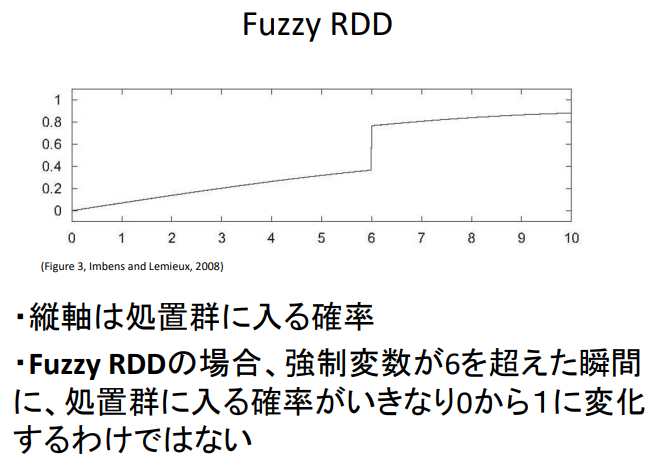
Fuzzy RDD
- 세로축은 처리군에 들어갈 확률
- Fuzzy RDD의 경우, 강제변수가 6을 초과하는 순간 처리군에 들어갈 확률이 갑자기 0에서 1로 바뀌는 것은 아니다.
불연속 회귀분석의 장점
- 가정이 성립되면 경계선 부근에서 마치 RCT(무작위 비교 실험)가 진행되는 것과 같은 상황을 이용할 수 있다.

생일과 사망률의 관계
- 다음 모델을 생각해보자.
𝑌ᵢ = 𝛼 + 𝜌 𝐷ₐᵢ + 𝛽 𝑎ᵢ + 𝑢ᵢ
𝑌ᵢ = 𝛼 + 𝜌 𝐷ₐᵢ + 𝛽₁ 𝑎ᵢ + 𝛽₂ 𝑎ᵢ² + 𝑢ᵢ
𝑌 : 사망률
𝐷ₐ : 21세 이상 여부(더미 변수) 1 or 0
𝑎ᵢ : 연령 - 계수 ρ는 21세가 됨으로써 사망률이 점프하는지 여부를 파악한다.

생일과 사망률의 관계
- 통계패키지 STATA에서 작성된 데이터는 확장자가 .dta
→ 이를 R에서 사용하기 위해 다음 패키지를 다운로드한다.
#install.packages ( " haven " ) # to use stata dta file
library ( haven )
- 그리고 데이터를 임포트한다.
AEJfigs <- read_dta ( file = " AEJfigs.dta " )

생일과 사망률의 관계
- 변수의 정의:
agecell = 나이
all = 모든 사망 사례를 포함한 사망률 - 데이터 프레임 내 변수 이름은
names ( AEJfigs )
- 결손값 삭제
AEJfigs2 <- AEJfigs %>%
filter ( !is.na ( all ) )
na가 결손치이며, 결손치가 없는 것만 가져오라는 뜻

생일과 사망률의 관계
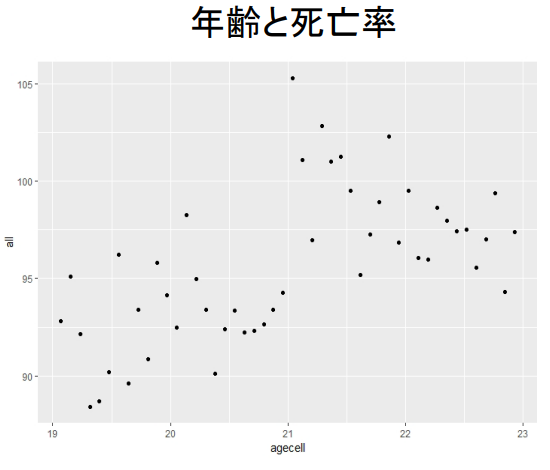
- 연령과 사망률의 관계를 도식화
age1 <- ggplot ( data = AEJfigs2 , aes ( x = agecell , y = all ) )
+ geom_point ( data = AEJfigs2 , aes ( x = agecell , y = all ) )

연령과 사망률
생일과 사망률의 관계
- 21세 이전 여부를 나타내는 변수 생성
AEJfigs2 $ over21 <- AEJfigs2 $ agecell >= 21

생일과 사망률의 관계
summary ( AEJfigs2 $ over21 )
Mode FALSE TRUE
logical 24 24
class ( AEJfigs2 $ over21 )
[1] "logical"

생일과 사망률의 관계
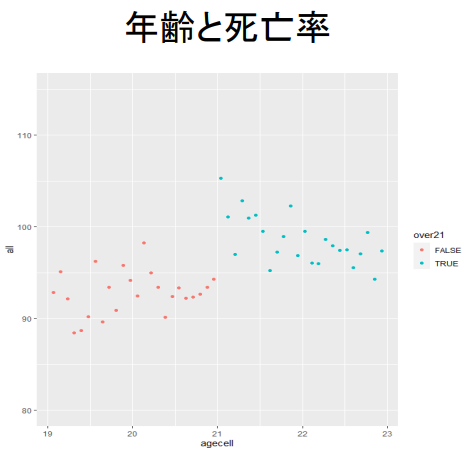
Age2 <- ggplot ( AEJfigs2 , aes ( x = agecell , y = all , colour = over21 ) )
+ geom_point ( )
+ ylim ( 80 , 115 )

연령과 사망률
생일과 사망률의 관계
- 앞의 두 가지 모델을 OLS로 추정
mlda1 <- lm ( all ~ agecell + over21 , data = AEJfigs2 )
summary ( mlda1 )
mlda2 <- lm ( all ~ agecell + I ( agecell^2 ) + over21 , data = AEJfigs2 )

생일과 사망률의 관계

불연속회귀분석 사례
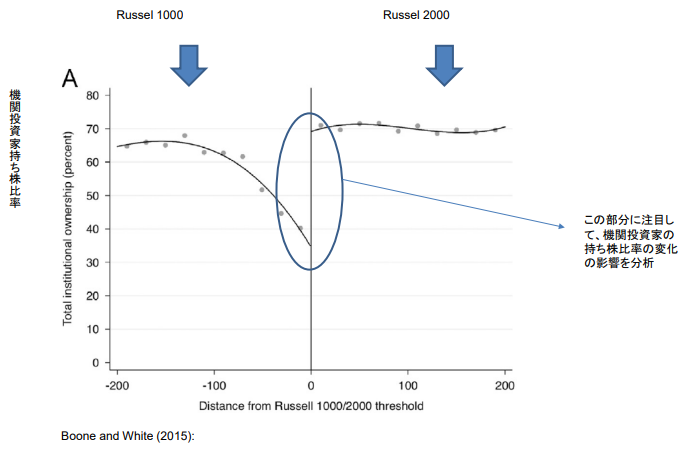
- Boone and White (2015):
기관투자자의 지분율 변화가 기업의 정보공개 태도에 영향을 미치는지 불연속회귀를 통해 분석 - 주가 지수 중 하나인 Russell1000과 2000의 구축방식의 특징에 주목하여
기관투자자 지분율과 관련하여 불연속성을 발견 - 불연속적 변화 전후의 기관투자자 지분율의 상승이 기업의 정보공개 정도 등의 상승을 가져온다는 것을 보여줌

Russell 1000/2000
- Russell1000과 Russell2000은 매년 일정 시점에 구성 종목을 교체한다.
- 어떤 종목이 Russell 1000에 들어갈지 Russell 2000에 들어갈지는 매년 5월 말 기준 시가총액에 따라 결정됨
- 시가총액이 큰 1000개 종목이 Russell1000에 편입된다.
- Russell1000과 Russell2000의 경계선에 있는 기업은
- 시가총액은 거의 동일
- Russell1000에 들어가면 시가총액이 가장 낮은 기업군에 들어가는 반면,
Russell2000에 들어가면 시가총액이 가장 높은 기업군에 들어간다.

이 부분에 주목하여 기관투자자 지분율 변화의 영향 분석
Y : 기관투자자 지분율(퍼센트)
X : 러셀 1000/2000 임계값과의 거리
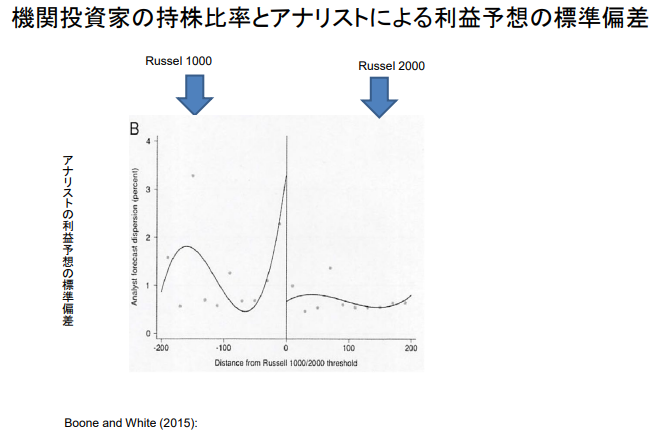
기관투자자 지분율과 애널리스트의 이익 예상치 표준편차 비교
Y : 애널리스트 이익 예상치의 표준편차
X : 러셀 1000/2000 임계값과의 거리
'WBS - 2023 Fall > 기업경제학 연습' 카테고리의 다른 글
| (기업경제 #10) 성향 점수를 사용하지 않는 매칭 | 복원 매칭과 비복원 매칭 (0) | 2023.12.14 |
|---|---|
| (기업경제 #9) Matching (0) | 2023.12.06 |
| (기업경제 #8) 로지트 모델(Logit Model)과 프로빗 모델(Probit Model) (0) | 2023.11.29 |
| (기업경제 #7) DID | Difference-in-Difference (차이의 차이 분석) (0) | 2023.11.16 |
| (기업경제 #6) 패널 분석 (Panel data analysis) (0) | 2023.11.09 |
| (기업경제 #5) 더미 변수를 이용한 분석 (0) | 2023.11.02 |
| (기업경제 #4) 이상치 처리 | 선형 회귀 모델(2) (0) | 2023.10.26 |
| (기업경제 #3) 선형회귀 Model (0) | 2023.10.19 |



