주식과 채권 수익률의 공통 위험 요인
유진 F. 파마와 케네스 R. 프렌치
시카고 대학교, 시카고, IL 60637, 미국
1992년 7월 접수, 1992년 9월 최종 버전 접수
이 논문은 주식과 채권 수익률에서 다섯 가지 공통 위험 요인을 식별합니다.
주식 시장 요인은 세 가지로, 전체 시장 요인과 기업 규모 및 장부가 대비 시장가치와 관련된 요인이 있습니다.
채권 시장 요인은 두 가지로, 만기와 디폴트 위험과 관련이 있습니다.
주식 수익률은 주식 시장 요인으로 인한 공통 변동성을 가지며, 채권 수익률과는 채권 시장 요인의 공통 변동성을 통해 연결됩니다.
저등급 회사채를 제외하고, 채권 시장 요인은 채권 수익률의 공통 변동성을 포착합니다.
가장 중요한 것은 이 다섯 가지 요인이 주식과 채권의 평균 수익률을 설명하는 것처럼 보인다는 것입니다.
1. 서론
미국 보통주 평균 수익률의 단면은 Sharpe(1964) 및 Lintner(1965)의 자산 가격 모델의 시장 베타 또는 Breeden(1979) 등의 시간 간 자산 가격 모델의 소비 베타와 거의 관련이 없습니다.
[예를 들어, Reinganum(1981) 및 Breeden, Gibbons, and Litzenberger(1989)를 참조하십시오.]
반면에, 자산 가격 이론에서 특별한 지위를 갖지 않는 변수들은 평균 수익률의 단면을 설명하는 신뢰할 수 있는 힘을 보여줍니다.
실증적으로 결정된 평균 수익률 변수 목록에는 규모(ME, 주가 곱하기 주식 수), 레버리지, 이익/주가(E/P), 장부가 대비 시장가치(기업의 보통주 장부가 BE와 시장가치 ME의 비율)가 포함됩니다.
[Banz(1981), Bhandari(1988), Basu(1983), Rosenberg, Reid, and Lanstein(1985)를 참조하십시오.]
파마와 프렌치(1992a)는 평균 주식 수익률의 단면에서 시장 베타, 규모, E/P, 레버리지, 장부가 대비 시장가치의 공동 역할을 연구합니다.
그들은 단독으로 사용하거나 다른 변수와 결합하여 사용하더라도, 시장 수익률에 대한 주식 수익률의 회귀의 기울기인 베타는 평균 수익률에 대한 정보를 거의 제공하지 않는다는 것을 발견했습니다.
단독으로 사용하면, 규모, E/P, 레버리지, 장부가 대비 시장가치는 설명력을 가집니다.
조합할 경우, 규모(ME)와 장부가 대비 시장가치(BE/ME)는 평균 수익률에서 레버리지와 E/P의 명백한 역할을 흡수하는 것으로 보입니다.
최종 결과는 두 개의 실증적으로 결정된 변수, 즉 규모와 장부가 대비 시장가치가 1963-1990년 기간 동안 NYSE, Amex, NASDAQ 주식의 평균 수익률의 단면을 잘 설명한다는 것입니다.
이 논문은 파마와 프렌치(1992a)의 자산 가격 테스트를 세 가지 방식으로 확장합니다.
- (a) 설명할 자산 수익률의 집합을 확장합니다.
파마와 프렌치(1992a)에서 고려한 유일한 자산은 보통주입니다.
시장이 통합되어 있다면, 단일 모델이 채권 수익률도 설명해야 합니다.
여기의 테스트는 주식뿐만 아니라 미국 정부와 회사채도 포함합니다. - (b) 수익률을 설명하는 데 사용되는 변수의 집합도 확장합니다.
파마와 프렌치(1992a)의 규모와 장부가 대비 시장가치 변수는 주식에 초점을 맞추고 있습니다.
우리는 채권 수익률에서 역할을 할 가능성이 있는 기간 구조 변수를 목록에 추가합니다.
목표는 채권 수익률에서 중요한 변수가 주식 수익률을 설명하는 데 도움이 되는지, 반대의 경우도 마찬가지인지를 조사하는 것입니다.
시장이 통합되어 있다면, 채권과 주식의 수익률 과정 사이에 아마도 겹침이 있을 것입니다. - (c) 아마도 가장 중요한 것은 자산 가격 모델을 테스트하는 접근 방식이 다르다는 것입니다.
파마와 프렌치(1992a)는 Fama와 MacBeth(1973)의 단면 회귀를 사용합니다.
주식 수익률의 단면은 평균 수익률을 설명한다고 가정되는 변수에 회귀됩니다.
정부 및 회사채에 대해 크기와 장부가 대비 시장가치와 같은 설명 변수가 명확한 의미를 가지지 않기 때문에 채권을 단면 회귀에 추가하는 것은 어려울 것입니다.
이 논문은 Black, Jensen, and Scholes(1972)의 시계열 회귀 접근 방식을 사용합니다.
주식과 채권의 월간 수익률은 주식의 시장 포트폴리오 수익률과 크기, 장부가 대비 시장가치(BE/ME), 수익률의 기간 구조 위험 요인을 모방하는 포트폴리오 수익률에 회귀됩니다.
시계열 회귀의 기울기는 크기나 BE/ME와 달리 주식뿐만 아니라 채권에 대한 위험 요인 민감도로 명확한 해석을 가집니다.
시계열 회귀는 두 가지 중요한 자산 가격 문제를 연구하는 데도 편리합니다.
- (a) 우리의 중심 주제 중 하나는 자산이 합리적으로 가격이 매겨진다면, 크기 및 장부가 대비 시장가치와 같은 평균 수익률과 관련된 변수는 수익률의 공통(공유되고 따라서 분산 불가능한) 위험 요인에 대한 민감도를 대리해야 한다는 것입니다.
시계열 회귀는 이 문제에 대한 직접적인 증거를 제공합니다.
특히, 기울기와 R² 값은 크기 및 BE/ME와 관련된 위험 요인의 모방 포트폴리오가 다른 요인으로 설명되지 않는 주식 및 채권 수익률의 공유 변동성을 포착하는지를 보여줍니다. - (b) 시계열 회귀는 초과 수익률(월간 주식 또는 채권 수익률에서 1개월 국채 수익률을 뺀 값)을 종속 변수로 사용하고, 초과 수익률 또는 무투자 포트폴리오의 수익률을 설명 변수로 사용합니다.
이러한 회귀에서 잘 명시된 자산 가격 모델은 0과 구별할 수 없는 절편을 생성합니다 [Merton(1973)].
추정된 절편은 간단한 수익률 측정치와 다양한 공통 요인의 조합이 평균 수익률의 단면을 얼마나 잘 포착하는지를 검증하는 공식적인 테스트를 제공합니다.
더욱이, 초과 수익률 회귀의 절편을 기준으로 자산 가격 모델을 평가하는 것은 엄격한 기준을 부과합니다.
경쟁 모델은 1개월 국채 수익률뿐만 아니라 장기 채권 및 주식의 수익률도 설명해야 합니다.
우리의 주요 결과는 요약하기 쉽습니다.
주식의 경우, 크기 및 BE/ME와 관련된 위험 요인을 모방하는 포트폴리오로 구성된 포트폴리오는 시계열 회귀에 무엇이 포함되든 관계없이 강한 공통 변동성을 포착합니다.
이는 크기와 장부가 대비 시장가치가 실제로 주식 수익률의 공통 위험 요인에 대한 민감도를 대리한다는 증거입니다.
또한, 우리가 조사한 주식 포트폴리오의 경우, 초과 시장 수익률과 크기 및 BE/ME 요인에 대한 모방 수익률을 포함하는 세 가지 요인 회귀의 절편은 거의 0에 가깝습니다.
따라서 시장 요인과 크기 및 장부가 대비 시장가치 관련 위험 요인의 대리변수는 평균 주식 수익률의 단면을 잘 설명하는 것처럼 보입니다.
주식에 대한 시계열 회귀의 해석은 흥미롭습니다.
Fama와 French(1992a)의 단면 회귀와 마찬가지로, 시계열 회귀는 크기 및 장부가 대비 시장가치 요인이 주식 간 평균 수익률의 차이를 설명할 수 있다고 말합니다.
그러나 이 요인들만으로는 주식과 1개월 국채 간 평균 수익률의 큰 차이를 설명할 수 없습니다.
이 작업은 시장 요인에 남겨져 있습니다.
크기 및 장부가 대비 시장가치 요인을 포함하는 회귀에서, 모든 주식 포트폴리오는 시장 요인에 대한 기울기가 거의 1에 가깝습니다.
그런 다음 시장 요인의 위험 프리미엄은 주식과 국채 간 평균 수익률을 연결합니다.
채권의 경우, 두 가지 기간 구조 요인(기간 프리미엄 및 디폴트 프리미엄)에 대한 모방 포트폴리오는 정부 및 회사채 포트폴리오의 수익률 변동성 대부분을 포착합니다.
기간 구조 요인은 채권의 평균 수익률도 '설명'하지만, 기간 구조 요인의 평균 프리미엄은 평균 초과 채권 수익률과 마찬가지로 0에 가깝습니다.
따라서 모든 회사채 및 정부채 포트폴리오가 동일한 장기 기대 수익률을 가진다는 가설도 기각할 수 없습니다.
주식 수익률의 공통 변동성은 주식 포트폴리오 수익률 세 가지에 의해 대부분 포착되며, 채권 수익률의 공통 변동성은 채권 포트폴리오 수익률 두 가지에 의해 대부분 설명됩니다.
그러나 주식 및 채권 시장은 확률적으로 분리되지 않습니다.
시계열 회귀에서 단독으로 사용될 때, 기간 구조 요인은 주식 수익률의 강한 변동성을 포착합니다;
실제로 주식에 대한 회귀에서의 기간 구조 요인에 대한 기울기는 채권과 매우 유사합니다.
하지만 흥미롭게도 주식 시장 요인도 회귀에 포함되면, 모든 주식 포트폴리오는 수익률의 두 가지 기간 구조 요인과 시장 요인에 대해 거의 동일한 방식으로 로딩됩니다.
결과적으로, 주식의 시장 포트폴리오는 시장 요인 및 두 가지 기간 구조 요인과 관련된 주식 수익률의 공통 변동성을 포착합니다.
채권과 주식 시장 간의 확률적 연결은 주로 기간 구조 요인에서 비롯되는 것처럼 보입니다.
단독으로 사용될 때, 초과 시장 수익률 및 크기 및 장부가 대비 시장가치 요인에 대한 모방 수익률은 채권 수익률의 공통 변동성을 포착하는 것처럼 보입니다.
그러나 두 가지 기간 구조 요인이 채권 회귀에 포함되면, 저등급 회사채를 제외한 모든 채권에 대해 주식 시장 요인의 설명력이 사라집니다.
한마디로, 우리의 결과는 수익률에 적어도 세 가지 주식 시장 요인과 두 가지 기간 구조 요인이 있다는 것을 시사합니다.
주식 수익률은 세 가지 주식 시장 요인으로 인한 공통 변동성을 가지며, 두 가지 기간 구조 요인의 공통 변동성을 통해 채권 수익률과 연결됩니다.
저등급 회사채를 제외하고는, 두 가지 기간 구조 요인만이 정부 및 회사채 수익률의 공통 변동성을 생성하는 것처럼 보입니다.
이야기는 다음과 같이 진행됩니다.
우리는 먼저 시계열 회귀의 입력을 소개합니다:
설명 변수와 설명할 수익률(섹션 2 및 3).
그런 다음 우리는 두 가지 주요 자산 가격 문제를 해결하기 위해 회귀를 사용합니다:
다양한 변수 조합이 (a) 채권 및 주식 수익률의 시간에 따른 공통 변동성을 어떻게 포착하는지(섹션 4) 및 (b) 평균 수익률의 단면을 어떻게 포착하는지(섹션 5).
2. 시계열 회귀의 입력
시계열 회귀의 설명 변수에는 주식의 시장 포트폴리오 수익률과 수익률에서 크기, 장부가 대비 시장가치, 기간 구조 요인을 모방하는 포트폴리오가 포함됩니다.
설명할 수익률은 두 가지 만기 범위의 정부채 포트폴리오, 다섯 가지 등급 그룹의 회사채 포트폴리오, 그리고 크기와 장부가 대비 시장가치를 기준으로 형성된 25개의 주식 포트폴리오입니다.
2.1 설명 수익률
설명 변수는 채권 수익률 변동성을 포착하는 데 중요한 것으로 예상되는 것들과 주식에 중요한 것으로 예상되는 것으로 두 세트로 나뉩니다.
이와 같은 방식으로 설명 변수를 구분하면 주식 수익률에 중요한 요인이 채권 수익률을 설명하는 데 도움이 되는지, 그 반대의 경우도 테스트할 수 있습니다.
2.1.1 채권 시장 요인
채권 수익률의 공통 위험 중 하나는 예상치 못한 금리 변동에서 발생합니다.
이 요인에 대한 우리의 대리 변수, TERM은 매월 장기 정부채 수익률(Ibbotson Associates에서 제공)과 이전 달 말에 측정된 1개월 국채 수익률(CRSP에서 제공)의 차이입니다.
국채 수익률은 채권의 예상 수익률의 일반적인 수준을 대리하기 위한 것이며, 따라서 TERM은 금리 변동으로 인한 장기 채권 수익률의 예상 수익률에서의 편차를 대리합니다.
회사채의 경우, 디폴트 가능성을 변화시키는 경제 조건의 변화는 수익률에 또 다른 공통 요인을 제공합니다.
이 디폴트 요인에 대한 우리의 대리 변수, DEF는 장기 회사채의 시장 포트폴리오 수익률(Ibbotson Associates의 회사채 모듈의 Composite 포트폴리오)과 장기 정부채 수익률의 차이입니다.
Chen, Roll, and Ross(1986)는 TERM과 DEF와 유사한 변수를 사용하여 NYSE 주식의 평균 수익률의 단면을 설명합니다.
그들은 Fama와 MacBeth(1973)의 단면 회귀 접근 방식을 사용합니다:
평균 주식 수익률의 단면은 TERM, 디폴트 요인 및 기타 요인의 시계열 회귀의 기울기의 단면으로 설명됩니다.
그들의 테스트에서 디폴트 요인은 평균 주식 수익률에서 가장 강력한 요인이며, TERM도 때때로 힘을 발휘합니다.
우리는 TERM과 DEF의 궤적이 주식 수익률의 시계열 변동에서 명확하게 나타난다는 것을 확인합니다.
우리는 또한 두 변수가 정부 및 회사채 수익률의 공통 변동성을 지배한다는 것을 발견합니다.
그러나 Chen, Roll, and Ross의 단면 회귀와는 대조적으로, 우리의 시계열 회귀는 DEF와 TERM 위험의 평균 프리미엄이 평균 주식 수익률의 단면에서의 변동을 설명하기에는 너무 작다고 말합니다.
[Shanken과 Weinstein(1990)도 유사한 점을 지적합니다.]
2.1.2 주식 시장 요인
동기 - 비록 크기와 장부가 대비 시장가치가 평균 주식 수익률을 설명하기 위한 임시변통 변수처럼 보일지라도, 우리는 그것들이 수익률의 공통 위험 요인을 대리할 것이라고 기대할 이유가 있습니다.
Fama와 French(1992b)에서 우리는 크기와 장부가 대비 시장가치가 경제적 기초와 관련이 있음을 문서화합니다.
놀랍지 않게도, 높은 BE/ME(장부가 대비 낮은 주가)를 가진 기업은 자산에 대한 낮은 수익을 가지는 경향이 있으며, 낮은 수익은 장부가 대비 시장가치가 측정되기 전과 후 최소 5년 동안 지속됩니다.
반대로, 낮은 BE/ME(장부가 대비 높은 주가)는 지속적으로 높은 수익과 관련이 있습니다.
크기는 또한 수익성과 관련이 있습니다.
장부가 대비 시장가치를 통제하면, 작은 기업은 큰 기업보다 자산에 대한 수익이 낮은 경향이 있습니다.
그러나 수익에서의 크기 효과는 주로 1980년대에 기인합니다.
1981년까지 BE/ME를 통제하면, 작은 기업은 큰 기업보다 약간 덜 수익성이 있습니다.
그러나 작은 기업의 경우, 1980-1982년의 경기 침체는 장기적인 수익 침체로 이어집니다.
어떤 이유에서인지, 작은 기업은 1980년대 중후반의 경제 호황에 참여하지 않습니다.
작은 기업이 큰 기업을 우회하는 장기 수익 침체를 겪을 수 있다는 사실은 크기가 크기와 평균 수익률 간의 부정적인 관계를 설명할 수 있는 공통 위험 요인과 관련이 있음을 시사합니다.
유사하게, 장부가 대비 시장가치와 수익 간의 관계는 상대적 수익성이 BE/ME와 평균 수익률 간의 긍정적인 관계를 설명할 수 있는 수익률의 공통 위험 요인의 출처임을 시사합니다.
크기 및 BE/ME와 관련된 수익률의 공통 변동성을 측정하는 것은 이 논문의 주요 과제입니다.
기초 블록 - 경제적 기초를 연구하기 위해, Fama와 French(1992b)는 ME와 BE/ME 정렬에서 주식을 정렬하여 형성된 여섯 개의 포트폴리오를 사용합니다.
우리는 여기서도 동일한 여섯 개의 포트폴리오를 사용하여 크기와 장부가 대비 시장가치와 관련된 수익률의 기초 위험 요인을 모방하기 위한 포트폴리오를 형성합니다.
이는 여기서 수행된 수익률의 공통 위험 요인 연구와 우리의 경제적 기초 연구 간의 일관성을 보장합니다.
1963년부터 1991년까지 매년 6월, CRSP의 모든 NYSE 주식은 크기(주가 곱하기 주식 수)로 정렬됩니다.
그런 다음 NYSE 중간 크기를 사용하여 NYSE, Amex, (1972년 이후) NASDAQ 주식을 두 그룹, 작은 그룹과 큰 그룹(S와 B)으로 나눕니다.
대부분의 Amex 및 NASDAQ 주식은 NYSE 중간값보다 작기 때문에 작은 그룹에는 비율적으로 많은 주식이 포함됩니다(1991년에는 13,616개 중 4,797개).
많은 수의 주식을 포함하고 있음에도 불구하고, 작은 그룹은 두 크기 그룹의 결합 가치의 절반보다 훨씬 적은 부분(1991년에는 약 8%)을 포함합니다.
우리는 또한 NYSE, Amex, NASDAQ 주식을 BE/ME의 순위 값의 하위 30%(낮음), 중간 40%(중간), 상위 30%(높음)에 대한 기준점을 기반으로 세 가지 장부가 대비 시장가치 그룹으로 나눕니다.
우리는 장부 보통주, BE를 주주의 장부 가치, 이연 법인세 및 투자 세액 공제(사용 가능한 경우)를 더하고, 우선주 장부 가치를 뺀 것으로 정의합니다.
사용 가능 여부에 따라, 우리는 상환, 청산, 액면가(이 순서로)를 사용하여 우선주의 가치를 추정합니다.
장부가 대비 시장가치, BE/ME는 회계 연도 t - 1에 끝나는 회계 연도의 장부 보통주를 t - 1년 12월 말의 시장가치로 나눈 것입니다.
우리는 BE가 음수인 기업을 사용하지 않으며, 이는 1980년 이전에는 드물며, BE/ME의 기준점을 계산하거나 크기-BE/ME 포트폴리오를 형성할 때 사용하지 않습니다.
또한, 일반 보통주(CRSP에 의해 분류된)를 가진 기업만 테스트에 포함됩니다.
이는 ADR, REIT 및 수익권 단위가 제외됨을 의미합니다.
기업을 BE/ME의 세 그룹과 ME의 두 그룹으로 정렬하기로 한 우리의 결정은 장부가 대비 시장가치가 평균 주식 수익률에서 크기보다 더 강한 역할을 한다는 Fama와 French(1992a)의 증거를 따릅니다.
분할은 임의적이지만, 우리는 대안을 탐색하지 않았습니다.
여기와 Fama와 French(1992b)에서의 테스트가 이러한 선택에 민감하지 않기를 바랍니다.
우리는 그것들이 그렇지 않다고 주장할 이유가 없습니다.
우리는 두 ME와 세 BE/ME 그룹의 교차점에서 여섯 개의 포트폴리오(S/L, S/M, S/H, B/L, B/M, B/H)를 구성합니다.
예를 들어, S/L 포트폴리오는 작은 ME 그룹에 있는 주식 중 낮은 BE/ME 그룹에 속하는 주식을 포함하며, B/H 포트폴리오는 큰 ME 주식 중 높은 BE/ME를 가진 주식을 포함합니다.
여섯 개 포트폴리오의 월간 가치 가중 수익률은 해마다 7월부터 다음 해 6월까지 계산되며, 포트폴리오는 t + 1년 6월에 다시 형성됩니다.
우리는 t - 1년의 장부 주식이 알려져 있는지 확인하기 위해 t년 7월에 수익률 계산을 시작합니다.
테스트에 포함되려면, 기업은 t - 1년 12월과 t년 6월의 CRSP 주가와 t - 1년의 COMPUSTAT 장부 보통주를 가져야 합니다.
더욱이, COMPUSTAT이 기업을 테이프에 추가하는 방식에 내재된 생존 편향을 피하기 위해 [Banz와 Breen(1986)], 우리는 기업이 COMPUSTAT에 2년 동안 나타날 때까지 포함하지 않습니다.
(COMPUSTAT은 기업을 추가할 때 2년 이상의 과거 데이터를 거의 포함하지 않는다고 말합니다).
크기 - 수익률의 크기와 관련된 위험 요인을 모방하기 위한 포트폴리오 SMB(작은 것에서 큰 것 뺀 것)는 매월 세 개의 작은 주식 포트폴리오(S/L, S/M, S/H)의 단순 평균 수익률과 세 개의 큰 주식 포트폴리오(B/L, B/M, B/H)의 단순 평균 수익률 간의 차이입니다.
따라서 SMB는 대략 같은 가중 평균 장부가 대비 시장가치를 가진 작은 주식 포트폴리오와 큰 주식 포트폴리오의 수익률 간의 차이입니다.
이 차이는 주로 BE/ME의 영향을 받지 않으며, 대신 작은 주식과 큰 주식의 다른 수익률 행동에 초점을 맞춥니다.
BE/ME - 장부가 대비 시장가치와 관련된 수익률의 위험 요인을 모방하기 위한 포트폴리오 HML(높은 것에서 낮은 것 뺀 것)은 유사하게 정의됩니다.
HML은 매월 두 개의 높은 BE/ME 포트폴리오(S/H 및 B/H)의 단순 평균 수익률과 두 개의 낮은 BE/ME 포트폴리오(S/L 및 B/L)의 평균 수익률 간의 차이입니다.
HML의 두 구성 요소는 대략 같은 가중 평균 크기를 가진 높은 BE/ME와 낮은 BE/ME 포트폴리오의 수익률입니다.
따라서 두 수익률 간의 차이는 주로 수익률의 크기 요인에서 자유로우며, 대신 높은 BE/ME와 낮은 BE/ME 기업의 다른 수익률 행동에 초점을 맞춥니다.
이 간단한 절차의 성공을 증명하듯이, 크기 및 장부가 대비 시장가치 요인의 1963-1991년 월간 모방 수익률 간의 상관계수는 -0.08에 불과합니다.
수익률의 공통 위험 요인에 대한 진정한 모방 포트폴리오는 기업별 요인의 분산을 최소화합니다.
SMB 및 HML의 여섯 개의 크기-BE/ME 포트폴리오는 가치 가중입니다.
가치 가중 구성 요소를 사용하는 것은 분산을 최소화하는 정신에 부합하며, 수익률 분산은 크기와 음의 관련이 있기 때문입니다(아래 표 1).
더 중요한 것은, 가치 가중 구성 요소를 사용하면 작은 주식과 큰 주식, 또는 높은 BE/ME와 낮은 BE/ME 주식의 다른 수익률 행동을 현실적인 투자 기회에 맞게 포착하는 모방 포트폴리오가 생성됩니다.
시장 - 마지막으로, 주식 수익률의 시장 요인에 대한 우리의 대리 변수는 초과 시장 수익률, RM-RF입니다.
RM은 여섯 개의 크기-BE/ME 포트폴리오에 있는 주식의 가치 가중 포트폴리오 수익률과 포트폴리오에서 제외된 음의 BE 주식을 포함한 것입니다.
RF는 1개월 국채 수익률입니다.
2.2 설명할 수익률
채권 - 시계열 회귀에서 사용되는 종속 변수 집합에는 두 개의 정부채 및 다섯 개의 회사채 포트폴리오의 초과 수익률이 포함됩니다.
정부채 포트폴리오(CRSP에서 제공)는 1년에서 5년, 6년에서 10년의 만기를 다룹니다.
다섯 개의 회사채 포트폴리오는 Moody's 등급 그룹 Aaa, Aa, A, Baa 및 LG(저등급, 즉 Baa 이하)로, Ibbotson Associates의 회사채 모듈(우리에게는 Dimensional Fund Advisors에서 제공)에서 가져왔습니다.
주식 - 주식의 경우, 우리는 크기와 장부가 대비 시장가치로 형성된 25개의 포트폴리오의 초과 수익률을 시계열 회귀의 종속 변수로 사용합니다.
우리는 크기와 BE/ME로 형성된 포트폴리오를 사용하여 모방 포트폴리오 SMB와 HML이 크기 및 장부가 대비 시장가치와 관련된 주식 수익률의 공통 요인을 포착하는지 여부를 결정하려고 합니다.
크기와 BE/ME로 형성된 포트폴리오는 경쟁 자산 가격 방정식에 의해 설명될 평균 수익률의 넓은 범위를 생성할 것입니다 [Fama와 French(1992a)].
그러나 나중에 우리는 E/P(이익/주가) 및 D/P(배당/주가)로 형성된 포트폴리오를 사용하여 우리의 설명 요인이 평균 수익률의 단면을 포착하는 능력에 대한 결과의 강건성을 확인합니다 [예: Keim(1988)].
25개의 크기 - BE/ME 포트폴리오는 앞서 논의된 여섯 개의 크기-BE/ME 포트폴리오와 유사하게 형성됩니다.
매년 6월, 우리는 NYSE 주식을 크기와 (독립적으로) 장부가 대비 시장가치로 정렬합니다.
크기 정렬의 경우, ME는 6월 말에 측정됩니다.
장부가 대비 시장가치 정렬의 경우, ME는 t - 1년 12월 말의 시장가치이며, BE는 t - 1년 회계 연도에 끝나는 장부 보통주입니다.
우리는 ME 및 BE/ME에 대한 NYSE 기준점을 사용하여 NYSE, Amex 및 (1972년 이후) NASDAQ 주식을 다섯 개의 크기 5분위와 다섯 개의 장부가 대비 시장가치 5분위로 할당합니다.
우리는 크기와 BE/ME 5분위의 교차점에서 25개의 포트폴리오를 구성하고 t년 7월부터 t + 1년 6월까지 포트폴리오의 가치 가중 월간 수익률을 계산합니다.
1963년 7월부터 1991년 12월까지 이 25개의 포트폴리오의 초과 수익률은 시계열 회귀에서 주식의 종속 변수입니다.
표 1은 25개의 크기-BE/ME 포트폴리오를 형성하기 위해 NYSE 기준점을 사용하기 때문에 가장 작은 크기 5분위의 포트폴리오에 가장 많은 주식(대부분 작은 Amex 및 NASDAQ 주식)이 포함되어 있음을 보여줍니다.
많은 주식을 포함하고 있음에도 불구하고, 가장 작은 크기 5분위의 다섯 개 포트폴리오 각각은 평균적으로 25개의 포트폴리오의 결합 주식 가치의 0.70% 미만입니다.
대조적으로, 가장 큰 크기 5분위의 포트폴리오는 가장 적은 주식을 가지고 있지만 가장 큰 가치 비율을 가지고 있습니다.
함께, 가장 큰 ME 5분위의 다섯 개 포트폴리오는 총 가치의 약 74%를 차지합니다.
가장 큰 크기 및 가장 낮은 BE/ME 5분위(성공적인 대기업)의 주식 포트폴리오는 25개의 포트폴리오의 결합 가치의 30% 이상을 차지합니다.
그리고 크기 5분위를 정의하기 위해 NYSE 주식만 사용하는 대신 모든 주식을 사용하는 것은 가장 큰 크기 5분위로의 가치 분포를 더욱 왜곡시킬 것입니다.
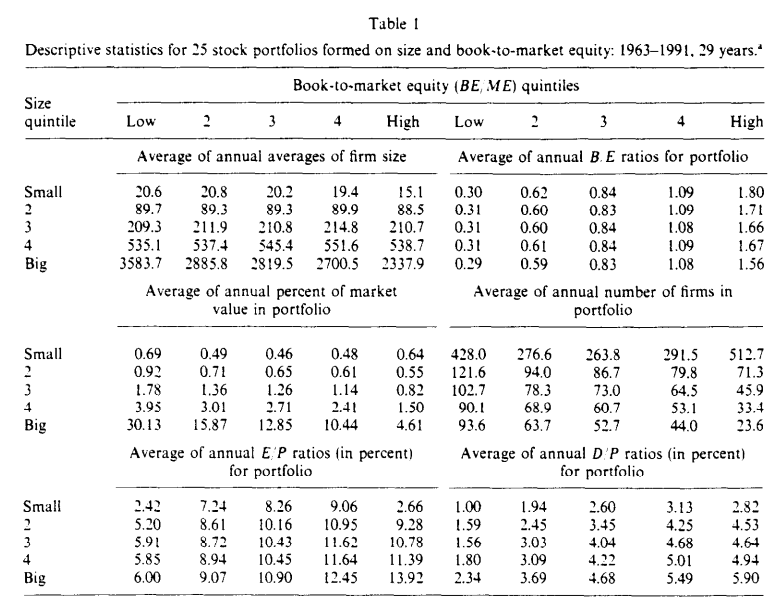
25개의 크기-BE/ME 주식 포트폴리오는 다음과 같이 형성됩니다.
1963년부터 1991년까지 매년 t마다, 6월 말에 측정된 크기(ME, 주가 곱하기 발행 주식 수)에 대한 NYSE 5분위 기준점을 사용하여 NYSE, Amex, NASDAQ 주식을 다섯 개의 크기 5분위로 할당합니다.
유사하게, BE/ME에 대한 NYSE 5분위 기준점을 사용하여 NYSE, Amex, NASDAQ 주식을 다섯 개의 장부가 대비 시장가치 5분위로 할당합니다. 25개의 크기-BE/ME 포트폴리오는 다섯 개의 크기 그룹과 다섯 개의 BE/ME 그룹의 교차점으로 형성됩니다.
장부 주식, BE는 주주의 장부 가치(COMPUSTAT), 대차대조표 이연 법인세 및 투자 세액 공제(사용 가능한 경우)를 더한 값에서 우선주 장부 가치를 뺀 것입니다.
사용 가능 여부에 따라, 우리는 상환, 청산, 액면가(이 순서로)를 사용하여 우선주의 장부 가치를 추정합니다.
주식의 장부가 대비 시장가치, BE/ME는 회계 연도 t - 1에 끝나는 회계 연도의 BE를 t - 1년 12월 말의 ME로 나눈 것입니다.
포트폴리오 형성 연도 t의 포트폴리오의 장부가 대비 시장가치, BE/ME는 회계 연도 t - 1에 끝나는 포트폴리오 내 기업의 장부 주식(BE)의 합을 t - 1년 12월의 시장가치(ME)의 합으로 나눈 것입니다.
포트폴리오의 이익/주가 비율(E/P) 연도 t는 회계 연도 t - 1에 끝나는 포트폴리오 내 기업의 주식 소득의 합을 t - 1년 12월의 시장가치의 합으로 나눈 것입니다.
주식 소득은 특별 항목 전 소득에 손익계산서 이연 법인세를 더하고 우선주 배당금을 뺀 것입니다.
포트폴리오의 배당 수익률(D/P) 연도 t는 t - 1년 7월부터 t년 6월까지 지급된 배당금의 합(포트폴리오 내 기업 간)을 t - 1년 6월의 시장가치의 합으로 나눈 것입니다.
우리는 배당금을 추정하기 위해 Fama와 French(1988)에서 설명한 절차를 사용합니다.
기술 통계는 1963년부터 1991년까지 매년 6월에 포트폴리오가 형성될 때 계산되며, 29년 동안 평균화됩니다.
표 1은 또한 가장 작은 크기 5분위를 제외한 모든 크기 5분위에서, 포트폴리오에 의해 차지하는 주식 수와 총 가치 비율이 낮은 BE/ME 포트폴리오에서 높은 BE/ME 포트폴리오로 감소함을 보여줍니다.
이 패턴에는 두 가지 원인이 있습니다.
첫째, 포트폴리오를 형성하기 위해 NYSE 주식의 독립적인 크기 및 장부가 대비 시장가치 정렬을 사용하는 것은 가장 높은 BE/ME 5분위가 가장 작은 주식으로 기울어져 있음을 의미합니다.
둘째, 대부분 작은 Amex 및 NASDAQ 주식은 유사한 크기의 NYSE 주식보다 낮은 장부가 대비 시장가치 비율을 가지는 경향이 있습니다.
즉, ME 측면에서 작은 NYSE 주식은 작은 Amex 및 NASDAQ 주식보다 타락한 천사(낮은 주가를 가진 대기업)일 가능성이 더 큽니다.
3. 경기장
표 2는 시계열 회귀에서의 종속 및 설명 수익률을 요약합니다.
종속 변수로 사용되는 포트폴리오의 평균 초과 수익률은 경쟁하는 위험 요인 세트가 설명해야 할 평균 수익률의 범위를 보여줍니다.
설명 포트폴리오의 평균 수익률은 수익률의 후보 공통 위험 요인에 대한 단위 위험당 평균 프리미엄(회귀 기울기)입니다.
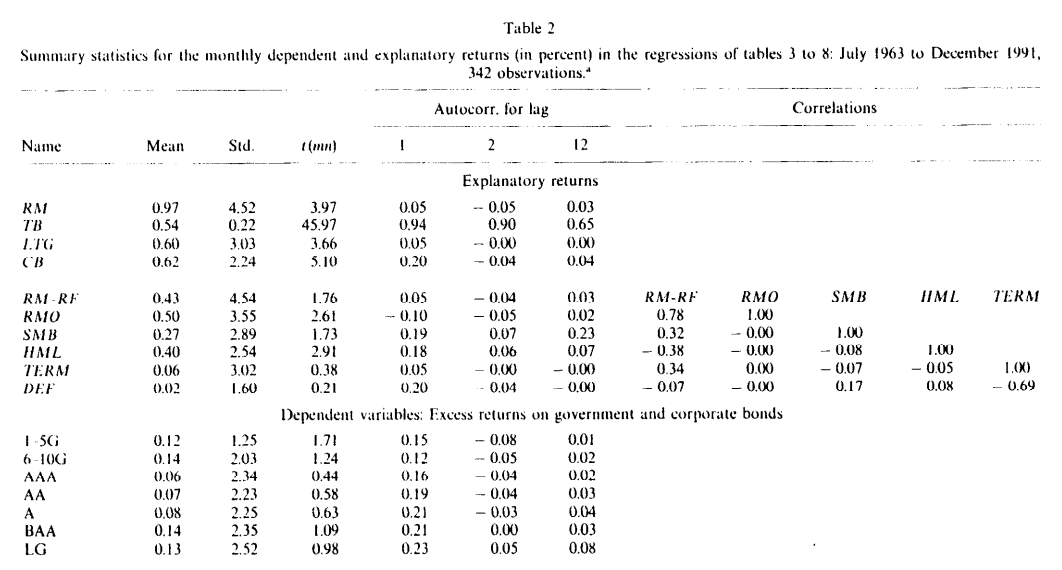
'RM'은 25개의 크기-BE/ME 포트폴리오에 포함된 주식의 가치 가중 월간 수익률에, 포트폴리오에서 제외된 음의 BE 주식을 더한 것입니다.
'RF'는 월 초에 관찰된 1개월 국채 수익률입니다.
'LTG'는 장기 정부채 수익률입니다.
'CB'는 장기 회사채의 시장 포트폴리오에 대한 대리 수익률입니다.
'TERM'은 LTG에서 RF를 뺀 값입니다.
'DEF'는 CB에서 LTG를 뺀 값입니다.
'SMB'(작은 것에서 큰 것 뺀 것)는 대략 같은 가중 평균 장부가 대비 시장가치를 가진 작은 주식 포트폴리오와 큰 주식 포트폴리오의 수익률 차이입니다.
'HML'(높은 것에서 낮은 것 뺀 것)은 대략 같은 가중 평균 크기를 가진 높은 장부가 대비 시장가치 포트폴리오와 낮은 장부가 대비 시장가치 포트폴리오의 수익률 차이입니다.
'RMO'는 RM - RF를 TERM, DEF, SMB, HML에 회귀한 회귀식 (1)의 절편과 잔차의 합입니다.
초과 수익률 회귀에서 종속 변수로 사용된 7개의 채권 포트폴리오는 1-5년 및 6-10년 정부채(1-5G 및 6-10G)와 Moody's에 의해 Aaa, Aa, A, Baa 및 Baa 이하(LG)로 평가된 회사채입니다.
25개의 크기-BE/ME 주식 포트폴리오는 다음과 같이 형성됩니다.
1963년부터 1991년까지 매년 t마다, 6월 말에 측정된 크기(ME, 주가 곱하기 발행 주식 수)에 대한 NYSE 5분위 기준점을 사용하여 NYSE, Amex, NASDAQ 주식을 다섯 개의 크기 5분위로 할당합니다.
유사하게, BE/ME에 대한 NYSE 5분위 기준점을 사용하여 NYSE, Amex, NASDAQ 주식을 다섯 개의 장부가 대비 시장가치 5분위로 할당합니다.
BE/ME에서, BE는 회계 연도 t - 1에 끝나는 장부 보통주이며, ME는 t - 1년 12월 말의 시장가치입니다.
25개의 크기-BE/ME 포트폴리오는 다섯 개의 크기 그룹과 다섯 개의 BE/ME 그룹의 교차점으로 형성됩니다.
포트폴리오의 가치 가중 월간 수익률은 매년 t의 7월부터 t + 1년의 6월까지 계산됩니다.
3.1 종속 수익률
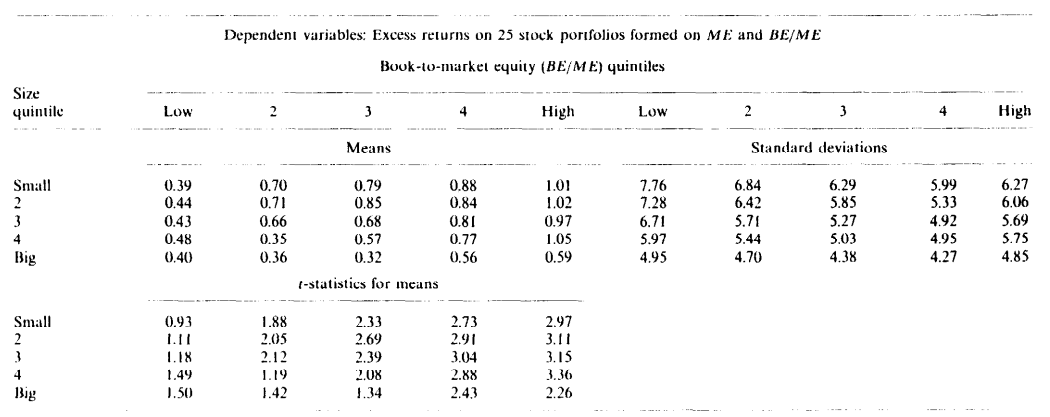
주식 - 크기와 장부가 대비 시장가치로 형성된 25개의 주식 포트폴리오는 월 0.32%에서 1.05%까지의 넓은 범위의 평균 초과 수익률을 생성합니다.
이 포트폴리오는 또한 크기와 평균 수익률 간의 부정적인 관계와 평균 수익률과 장부가 대비 시장가치 간의 더 강한 긍정적인 관계가 있음을 Fama-French(1992a) 증거로 확인합니다.
가장 낮은 BE/ME 5분위를 제외하고, 평균 수익률은 작은 크기 포트폴리오에서 큰 크기 포트폴리오로 갈수록 감소하는 경향이 있습니다.
평균 수익률과 장부가 대비 시장가치 간의 관계는 더 일관성이 있습니다.
모든 크기 5분위에서 평균 수익률은 BE/ME와 함께 증가하는 경향이 있으며, 가장 높은 BE/ME 포트폴리오와 가장 낮은 BE/ME 포트폴리오 간의 평균 수익률 차이는 월 0.19%에서 0.62%까지입니다.
우리의 시계열 회귀는 수익률의 공통 위험 요인에 대한 프리미엄으로 평균 수익률의 단면을 설명하려고 합니다.
25개의 주식 포트폴리오의 넓은 범위의 평균 수익률과 평균 수익률의 크기 및 장부가 대비 시장가치 효과는 경쟁하는 위험 요인 세트에 흥미로운 도전을 제공합니다.
하위 두 BE/ME 5분위의 10개 포트폴리오 중 대부분은 평균 초과 수익률이 0에서 두 표준 오차 이내입니다.
이는 잘 알려진 문제의 예입니다 [Merton(1980)]:
주식 수익률은 높은 표준 편차(크기-BE/ME 포트폴리오의 경우 월 약 6%)를 가지기 때문에, 큰 평균 수익률이 종종 0과 신뢰할 수 있게 다르지 않습니다.
그러나 주식 수익률의 높은 변동성은 우리의 자산 가격 테스트가 힘이 부족하다는 것을 의미하지 않습니다.
수익률의 공통 요인은 주식 수익률의 대부분의 변동성을 흡수하여 시계열 회귀의 절편에서 자산 가격 테스트를 매우 정밀하게 만듭니다.
채권 - 주식 포트폴리오와 대조적으로, 표 2의 정부 및 회사채 포트폴리오의 평균 초과 수익률은 미미합니다.
모든 평균 초과 채권 수익률은 월 0.15% 미만이며, 7개 중 하나만이 0에서 1.5 표준 오차 이상입니다.
표 2에는 (a) 정부채의 평균 수익률이 만기와 함께 증가한다는 증거가 거의 없으며, (b) 장기 회사채가 정부채보다 평균 수익률이 높다는 증거가 없으며, (c) 회사채의 평균 수익률이 낮은 등급 그룹에서 더 높다는 증거가 없습니다.
평균 채권 수익률의 평탄한 단면은 자산 가격 테스트에서 채권이 흥미롭지 않은 종속 변수라는 것을 의미하지 않습니다.
반대로, 채권은 수익률의 공통 위험 요인에 대한 다른 기울기에 기반한 평균 수익률의 단면에서 패턴을 예측하는 자산 가격 방정식을 기각하는 데 좋은 후보입니다.
3.2 설명 수익률
자산 가격 테스트에 대한 시계열 회귀 접근 방식에서, 수익률의 공통 요인에 대한 평균 위험 프리미엄은 설명 변수의 평균 값입니다.
RM-RF의 평균 값(시장 베타 당 평균 프리미엄)은 월 0.43%입니다.
이는 투자 관점에서 큰 값(연간 약 5%)이지만, 0에서 1.76 표준 오차의 경계에 있습니다.
크기와 관련된 요인에 대한 평균 SMB 수익률은 월 0.27%에 불과합니다(t = 1.73).
그러나 25개 주식 포트폴리오에 대한 SMB의 기울기는 1.7을 초과하는 범위를 포괄하므로, 크기 요인으로 인한 예상 수익률의 추정 차이는 월 약 0.46%로 큽니다.
장부가 대비 시장가치 요인 HML은 월 0.40%의 평균 프리미엄을 생성하며(t = 2.91), 이는 실용적 및 통계적 측면에서 모두 큽니다.
기간 구조 요인의 평균 위험 프리미엄은 주식 시장 요인에 비해 사소합니다.
TERM(기간 프리미엄)과 DEF(디폴트 프리미엄)는 평균적으로 월 0.06%, 0.02%이며, 둘 다 0에서 0.3 표준 오차 이내입니다.
그러나 TERM과 DEF는 주식 시장 수익률 SMB 및 HML만큼 변동성이 큽니다.
낮은 평균 프리미엄은 TERM과 DEF가 평균 수익률의 단면에서 많은 변동성을 설명하지 못하게 하지만, 높은 변동성은 두 요인이 수익률의 상당한 공통 변동성을 포착할 수 있음을 의미합니다.
실제로, TERM과 DEF의 낮은 평균과 높은 변동성은 채권 수익률을 설명하는 데 유리할 것입니다.
그러나 평균 주식 수익률의 강한 단면 변동성을 설명하는 작업은 더 높은 평균 프리미엄을 생성하는 주식 시장 요인 RM-RF, SMB, HML에 맡겨집니다.
이제 자산 가격 테스트로 넘어갑니다.
시계열 회귀 접근 방식에서, 테스트는 두 부분으로 구성됩니다.
4절에서는 두 채권 시장 수익률 TERM과 DEF, 그리고 세 주식 시장 수익률 RM-RF, SMB, HML이 주식 및 채권 수익률에서 공통(공유되고 따라서 분산 불가능한) 변동성을 포착하는 위험 요인임을 확립합니다.
5절에서는 시계열 회귀의 절편을 사용하여 수익률의 공통 위험 요인에 대한 평균 프리미엄이 채권과 주식의 평균 수익률의 단면을 설명하는지 테스트합니다.
4. 수익률의 공통 변동성
시계열 회귀에서 기울기와 R² 값은 다양한 위험 요인이 채권과 주식 수익률의 공통 변동성을 포착하는지에 대한 직접적인 증거입니다.
우리는 먼저 채권 시장과 주식 시장 요인의 설명력을 개별적으로 조사합니다.
이는 주식과 채권 수익률의 확률적 과정 간의 겹침을 테스트하는 목적을 가집니다.
채권 수익률에서 중요한 채권 시장 요인이 주식 수익률의 공통 변동성을 포착하는지, 그 반대의 경우도 마찬가지인지 확인합니다.
그런 다음 채권 및 주식 시장 요인의 공동 설명력을 조사하여 수익률의 공통 변동성에 대한 전반적인 이야기를 발전시킵니다.
4.1. 채권 시장 요인
표 3은 시계열 회귀에서 설명 변수로 단독 사용될 때, TERM과 DEF가 주식과 채권 수익률의 공통 변동성을 포착한다는 것을 보여줍니다.
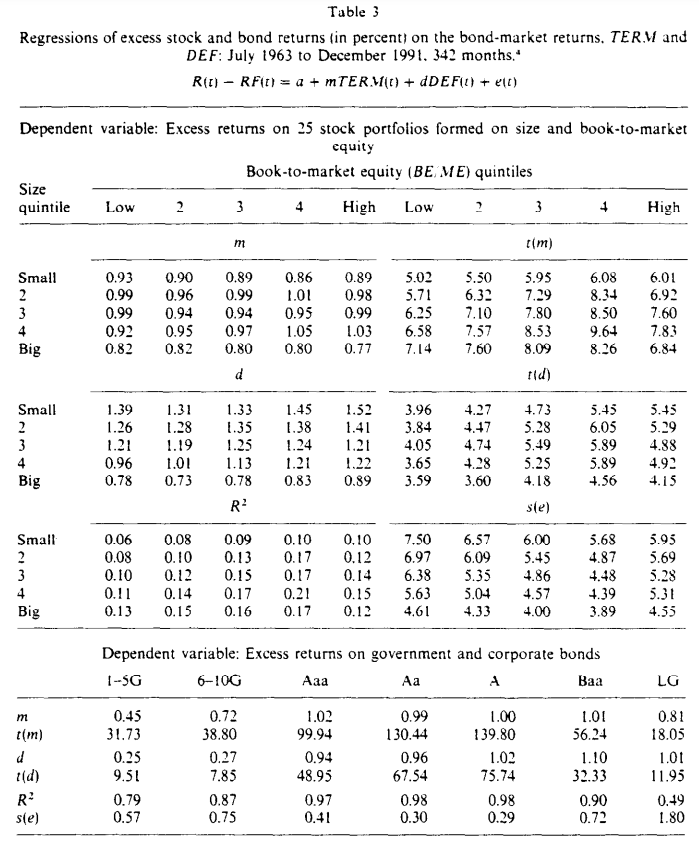
TERM은 LTG-RF로, LTG는 월간 장기 정부채 수익률이고 RF는 월 초에 관찰된 1개월 국채 수익률입니다.
DEF는 CB-LTG로, CB는 회사채의 시장 포트폴리오에 대한 대리 수익률입니다.
초과 수익률 회귀에서 종속 변수로 사용된 7개의 채권 포트폴리오는 1-5년 및 6-10년 정부채(I-5G 및 6-10G)와 Moody's에 의해 Aaa, Aa, A, Baa 및 Baa 이하(LG)로 평가된 회사채입니다.
25개의 크기-BE/ME 주식 포트폴리오는 다음과 같이 형성됩니다.
1963년부터 1991년까지 매년 t마다, 6월 말에 측정된 크기(ME, 주가 곱하기 발행 주식 수)에 대한 NYSE 5분위 기준점을 사용하여 NYSE, Amex, NASDAQ 주식을 다섯 개의 크기 5분위로 할당합니다.
유사하게, BE/ME에 대한 NYSE 5분위 기준점을 사용하여 NYSE, Amex, NASDAQ 주식을 다섯 개의 장부가 대비 시장가치 5분위로 할당합니다.
BE/ME에서, BE는 회계 연도 t - 1에 끝나는 장부 보통주이며, ME는 t - 1년 12월 말의 시장가치입니다.
25개의 크기-BE/ME 포트폴리오는 다섯 개의 크기 그룹과 다섯 개의 BE/ME 그룹의 교차점으로 형성됩니다.
포트폴리오의 가치 가중 월간 수익률은 매년 t의 7월부터 t + 1년의 6월까지 계산됩니다.
R² 및 잔차 표준 오차 s(e)는 자유도를 조정하여 계산됩니다.
25개의 주식 포트폴리오는 TERM에 대해 모두 0보다 5 표준 오차 이상 큰 기울기를 생성하며, 7개의 채권 포트폴리오 중 가장 작은 TERM 기울기도 0에서 18 표준 오차입니다.
DEF에 대한 기울기는 채권의 경우 모두 7.8 표준 오차 이상이며, 주식의 경우 3.5 표준 오차 이상입니다.
TERM과 DEF의 기울기는 기간 구조 변수를 통해 주식과 채권 수익률의 공통 변동성을 직접 비교할 수 있게 합니다.
흥미롭게도, TERM과 DEF가 포착한 공통 변동성은 주식에서 채권보다 더 강합니다.
주식의 대부분의 DEF 기울기는 채권의 그것보다 큽니다.
주식의 TERM 기울기(모두 1에 가까움)는 채권이 생성한 가장 큰 기울기와 유사합니다.
예상대로 TERM과 DEF가 설명하는 수익률 분산의 비율은 채권에서 더 높습니다.
채권 회귀에서 R²는 저등급 회사채의 경우 0.49에서 고등급 회사채의 경우 0.97 및 0.98까지 범위입니다.
대조적으로, 주식의 R²는 0.06에서 0.21까지 범위입니다.
따라서 TERM과 DEF는 주식과 채권 수익률의 공유 변동성을 명확히 식별하지만, 주식과 저등급 채권의 경우 주식 시장 요인으로 설명해야 할 변동성이 많이 남아 있습니다.
TERM의 기울기에는 흥미로운 패턴이 있습니다. 기울기는 1-5년 및 6-10년 정부채에서 0.45에서 0.72로 증가하고, 그 후 5개의 장기 회사채 포트폴리오 중 4개에서 1에 가까운 값에 정착합니다.
(기울기가 0.81인 저등급 포트폴리오 LG는 예외입니다.)
예상대로, 장기 채권은 TERM으로 측정된 금리 변동에 단기 채권보다 더 민감합니다.
그러나 놀라운 점은 25개의 주식 포트폴리오가 장기 채권과 유사한 TERM 기울기를 가진다는 것입니다.
이는 TERM이 포착한 위험이 장기 증권, 채권 및 주식에 대해 비슷한 방식으로 영향을 미치는 할인율 충격에서 비롯된다는 것을 시사합니다.
여기서 관찰된 TERM 기울기와 채권 및 주식 수익률을 예측하는 수익률 스프레드에 대한 우리의 이전 증거 사이에는 흥미로운 유사성이 있습니다.
Fama와 French(1989)에서, 우리는 장기 채권 수익률에서 단기 채권 수익률을 뺀 스프레드(TERM의 사전 버전)가 주식과 채권 수익률을 예측하고, 장기 채권과 주식의 예상 수익률에서 시간 경과에 따른 변동성을 거의 동일하게 포착한다는 것을 발견했습니다.
우리는 수익률 스프레드가 모든 장기 증권에 비슷한 방식으로 영향을 미치는 할인율 변화에 대한 기간 프리미엄의 변동성을 포착한다고 추측했습니다.
여기서 관찰된 장기 채권과 주식의 TERM 기울기는 그 추측과 일치하는 것 같습니다.
우리의 이전 연구는 또한 장기 채권 수익률에서 단기 채권 수익률을 뺀 스프레드로 예측된 수익률 프리미엄이 양수와 음수 값을 오가며 평균적으로 0에 가깝다는 것을 발견했습니다.
이는 여기서의 증거(표 2)와 유사하게, 금리 변동과 관련된 공통 위험에 대한 평균 프리미엄(TERM의 평균 값)이 0에 가깝다는 것을 보여줍니다.
표 3의 DEF 기울기 패턴도 흥미롭습니다.
작은 주식의 수익률은 큰 주식의 수익률보다 DEF가 포착한 위험에 더 민감합니다.
주식의 DEF 기울기는 회사채보다 크고, 회사채의 DEF 기울기는 정부채보다 큽니다.
따라서 DEF는 정부채에서 회사채로, 채권에서 주식으로, 큰 주식에서 작은 주식으로 증가하는 공통 '디폴트' 위험을 수익률에서 포착하는 것으로 보입니다.
다시 말해, 이 DEF 기울기 패턴과 Fama와 French(1989)에서 관찰된 유사한 패턴 사이에는 흥미로운 유사성이 있습니다.
Fama-Macbeth(1973) 단면 회귀 접근 방식을 사용하고 크기 순위 값으로 형성된 주식 포트폴리오를 사용하여, Chan, Chen, Hsieh(1985) 및 Chen, Roll, Ross(1986)는 DEF와 같은 변수의 단면 기울기가 크기와 평균 주식 수익률 간의 부정적인 관계를 설명하는 데 큰 역할을 한다는 것을 발견했습니다.
표 3에서 크기와 DEF 기울기 간의 부정적인 관계를 감안할 때, DEF 기울기가 크기 포트폴리오에 대한 단면 수익률 회귀에서 잘 작동하는 이유를 쉽게 알 수 있습니다.
그러나 우리의 시계열 회귀는 DEF가 평균 주식 수익률에서 크기 효과를 설명할 수 없음을 시사합니다.
시계열 회귀에서 DEF 기울기 단위당 평균 프리미엄은 DEF의 평균인 월 0.02%에 불과합니다.
마찬가지로, TERM의 평균 수익률은 월 0.06%에 불과합니다.
결과적으로, TERM 및 DEF에 대한 주식 수익률 회귀의 절편은 평균 수익률에서 강력한 크기 및 장부가 대비 시장가치 효과를 남깁니다.
또한 주식 시장 요인을 회귀에 추가하면 표 3의 크기와 DEF 기울기 간의 부정적인 관계가 사라진다는 것을 발견할 것입니다.
4.2. 주식 시장 요인
수익률에서 주식 시장 요인의 역할은 세 단계로 개발됩니다.
우리는 (a) 초과 시장 수익률 RM-RF를 사용하여 초과 채권 및 주식 수익률을 설명하는 회귀, (b) 크기 및 장부가 대비 시장가치 요인에 대한 모방 수익률인 SMB 및 HML을 설명 변수로 사용하는 회귀, (c) RM-RF, SMB, HML을 사용하는 회귀를 조사합니다.
세 가지 요인 회귀는 주식에 대해 잘 작동하지만, 하나 및 두 가지 요인 회귀는 그 이유를 설명하는 데 도움이 됩니다.
시장 - 표 4는 놀랍지 않게도 주식의 시장 포트폴리오의 초과 수익률 RM-RF가 표 3의 기간 구조 요인보다 주식 수익률의 공통 변동성을 더 많이 포착한다는 것을 보여줍니다.
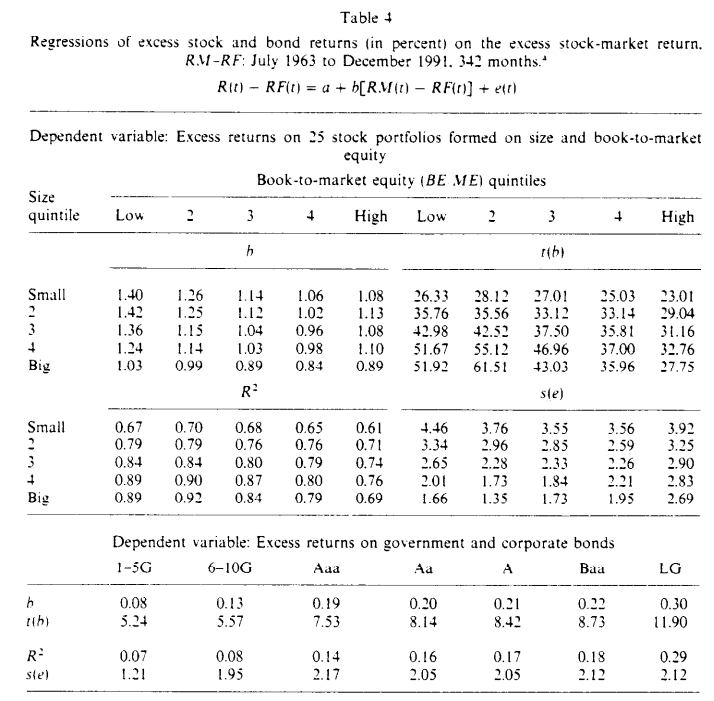
'RM'은 25개의 크기-BE/ME 포트폴리오에 포함된 모든 주식의 가치 가중 월간 수익률에, 25개 포트폴리오에서 제외된 음의 BE 주식을 더한 것입니다. 'RF'는 월 초에 관찰된 1개월 국채 수익률입니다.
초과 수익률 회귀에서 종속 변수로 사용된 7개의 채권 포트폴리오는 1-5년 및 6-10년 정부채(I-5G 및 6-10G)와 Moody's에 의해 Aaa, Aa, A, Baa 및 Baa 이하(LG)로 평가된 회사채입니다.
25개의 크기-BE/ME 주식 포트폴리오는 다음과 같이 형성됩니다. 1963년부터 1991년까지 매년 t마다, 6월 말에 측정된 크기(ME, 주가 곱하기 발행 주식 수)에 대한 NYSE 5분위 기준점을 사용하여 NYSE, Amex, NASDAQ 주식을 다섯 개의 크기 5분위로 할당합니다.
유사하게, BE/ME에 대한 NYSE 5분위 기준점을 사용하여 NYSE, Amex, NASDAQ 주식을 다섯 개의 장부가 대비 시장가치 5분위로 할당합니다.
BE/ME에서, BE는 회계 연도 t - 1에 끝나는 장부 보통주이며, ME는 t - 1년 12월 말의 시장가치입니다.
25개의 크기-BE/ME 포트폴리오는 다섯 개의 크기 그룹과 다섯 개의 BE/ME 그룹의 교차점으로 형성됩니다.
포트폴리오의 가치 가중 월간 수익률은 매년 t의 7월부터 t + 1년의 6월까지 계산됩니다.
R² 및 잔차 표준 오차 s(e)는 자유도를 조정하여 계산됩니다.
그러나 중요한 사실은 시장이 다른 요인으로 설명될 수 있는 주식 수익률에서 많은 변동성을 남긴다는 것입니다.
0.9에 가까운 유일한 R² 값은 큰 주식의 낮은 장부가 대비 시장가치 포트폴리오에 해당합니다.
작은 주식 및 높은 BE/ME 포트폴리오의 경우, R² 값이 0.8 또는 0.7 미만인 것이 일반적입니다.
이러한 주식 포트폴리오는 크기 및 장부가 대비 시장가치 요인인 SMB 및 HML이 한계 설명력을 보여줄 수 있는 최고의 기회를 가질 것입니다.
주식의 시장 포트폴리오는 또한 채권 수익률의 공통 변동성을 포착합니다.
시장 베타는 주식보다 채권에서 훨씬 작지만, 0에서 5에서 12 표준 오차입니다.
직관과 일치하게, 베타는 회사채가 정부채보다 높고, 저등급 채권이 고등급 채권보다 높습니다.
저등급 채권(LG)의 베타는 0.30이며, RM-RF는 LG 수익률의 분산의 19%를 깔끔하게 설명합니다.
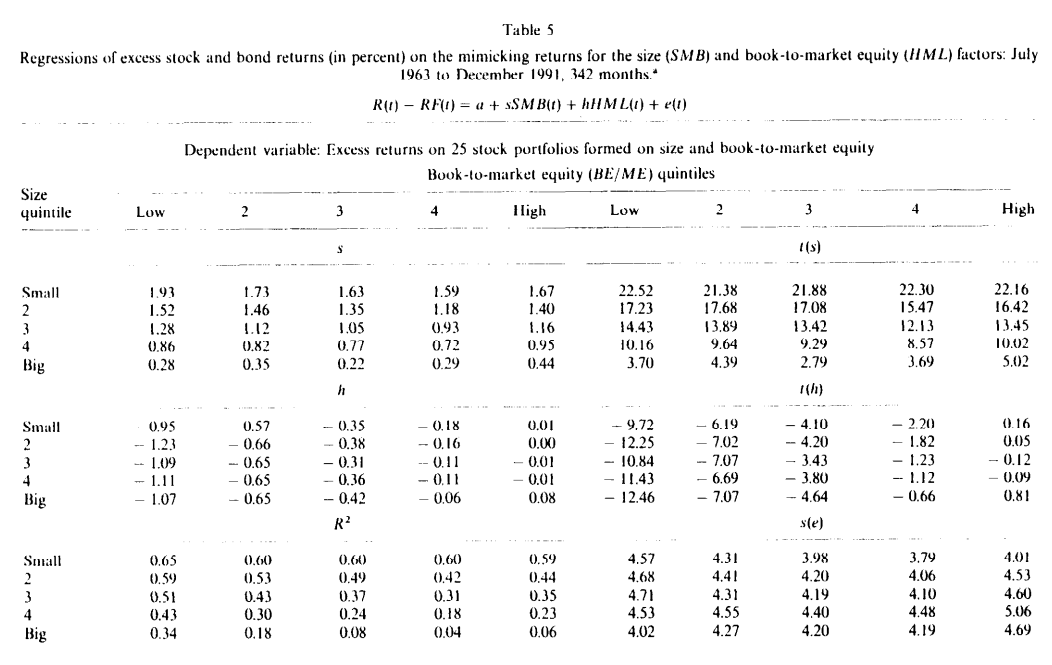
SMB 및 HML - 표 5는 시장 포트폴리오와의 경쟁이 없는 경우 SMB 및 HML이 주식 수익률에서 상당한 시계열 변동성을 포착한다는 것을 보여줍니다.
25개의 R² 값 중 20개가 0.2 이상이고 8개가 0.5 이상입니다.
그러나 특히 더 큰 크기 5분위의 포트폴리오의 경우, SMB 및 HML은 표 4의 시장 포트폴리오가 포착하는 주식 수익률의 공통 변동성을 남깁니다.
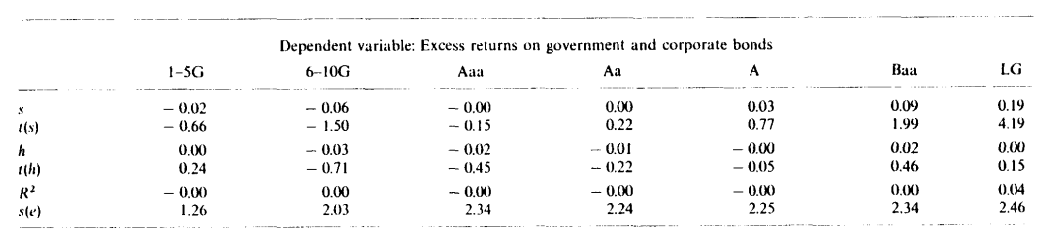
시장, SMB 및 HML - 표 5는 SMB 및 HML이 단독으로 사용될 때 채권 수익률을 설명할 힘이 거의 없음을 보여줍니다.
표 6은 초과 시장 수익률이 회귀에 포함될 때, 세 가지 주식 시장 요인 각각이 채권 수익률의 변동성을 포착한다는 것을 보여줍니다.
그러나 채권 회귀에 기간 구조 요인을 추가하면 주식 시장 요인의 설명력이 대부분 사라질 것입니다.
따라서 표 6에서 채권 수익률에서 주식 시장 요인의 명백한 역할은 아마도 기간 구조 요인과 주식 시장 요인 간의 공변동에서 비롯된 것일 것입니다.
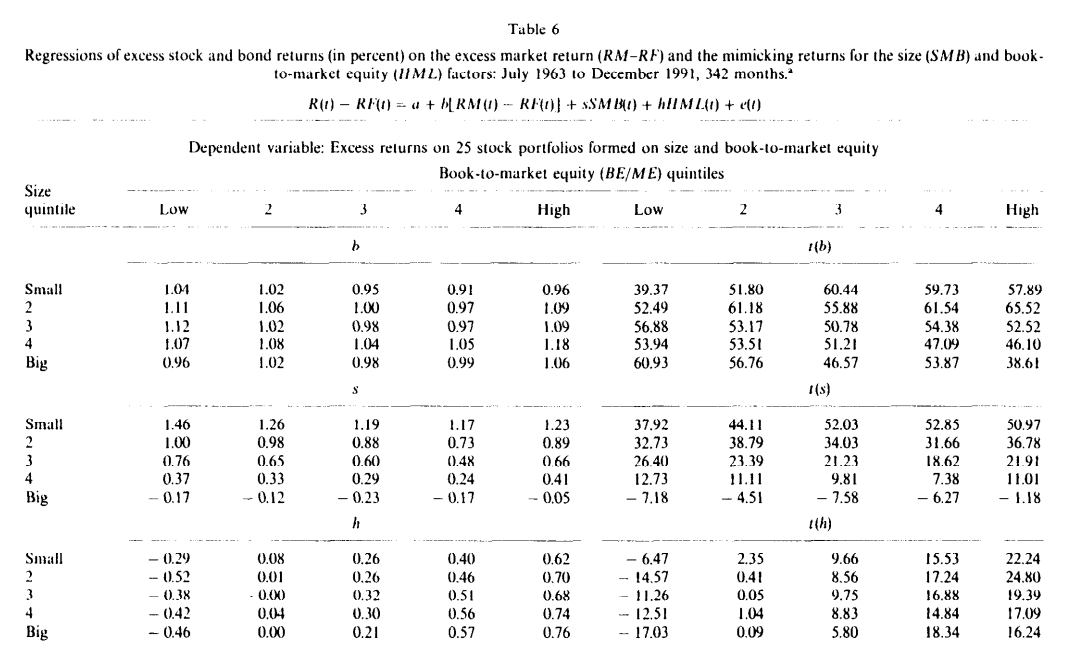
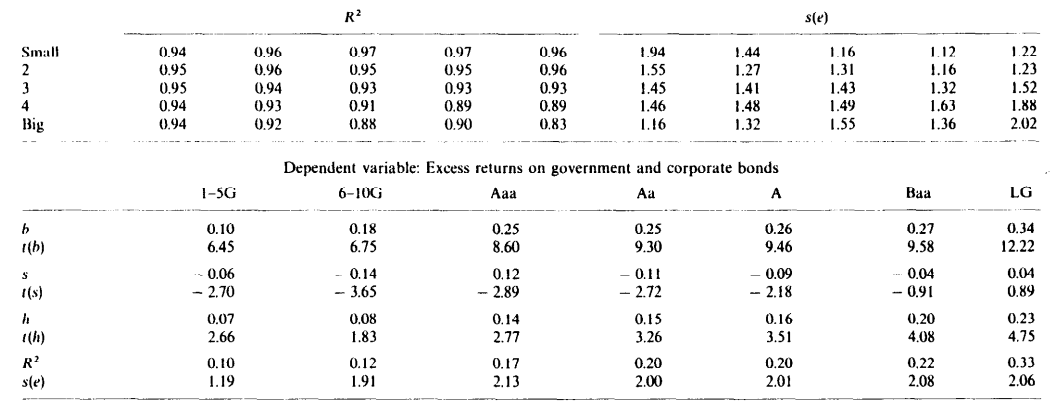
표 6에서 흥미로운 회귀는 주식에 대한 것입니다.
놀랍지 않게도, 세 가지 주식 시장 요인은 주식 수익률의 강력한 공통 변동성을 포착합니다.
주식의 시장 베타는 모두 0에서 38 표준 오차 이상입니다.
한 가지 예외를 제외하고, 주식의 SMB 기울기에 대한 t-통계는 4보다 크며, 대부분은 10보다 큽니다.
크기 요인에 대한 모방 수익률인 SMB는 시장과 HML이 놓친 주식 수익률의 공유 변동성을 명확하게 포착합니다.
더욱이, 주식의 SMB 기울기는 크기와 관련이 있습니다.
모든 장부가 대비 시장가치 5분위에서 SMB 기울기는 작은 크기 5분위에서 큰 크기 5분위로 단조롭게 감소합니다.
유사하게, 장부가 대비 시장가치 요인에 대한 모방 수익률인 HML의 기울기는 BE/ME와 체계적으로 관련이 있습니다.
주식의 모든 크기 5분위에서, HML 기울기는 가장 낮은 BE/ME 5분위의 강한 음수 값에서 가장 높은 BE/ME 5분위의 강한 양수 값으로 단조롭게 증가합니다.
두 번째 BE/ME 5분위(기울기가 음수에서 양수로 바뀌는 곳)를 제외하고, HML 기울기는 0에서 5 표준 오차 이상입니다.
HML은 장부가 대비 시장가치와 관련된 주식 수익률의 공유 변동성을 명확하게 포착하며, 이는 시장과 SMB가 놓친 것입니다.
주식의 SMB 및 HML에 대한 강력한 기울기를 감안할 때, 두 수익률을 회귀에 추가하면 R²가 크게 증가하는 것은 놀라운 일이 아닙니다.
주식의 경우, 시장만으로는 25개 중 두 개의 R² 값만이 0.9 이상을 생성합니다(표 4);
세 가지 요인 회귀(표 6)에서는 R² 값이 0.9 이상인 것이 일반적입니다(25개 중 21개).
가장 작은 크기 5분위의 다섯 개 포트폴리오의 경우, R²는 표 4에서 0.61에서 0.70 사이의 값에서 표 6에서 0.94에서 0.97 사이의 값으로 증가합니다.
가장 큰 크기 및 가장 높은 BE/ME 5분위의 포트폴리오에 대한 가장 낮은 세 가지 요인 R²인 0.83도 시장만으로 생성된 0.69보다 훨씬 큽니다.
회귀에 SMB 및 HML을 추가하면 주식의 시장 베타에 흥미로운 영향을 미칩니다.
표 4의 한 가지 요인 회귀에서, 가장 작은 크기 및 가장 낮은 BE/ME 5분위의 주식 포트폴리오의 베타는 1.40입니다.
다른 극단에서는, 가장 큰 크기 및 가장 높은 BE/ME 5분위의 주식 포트폴리오의 단변량 베타는 0.89입니다.
표 6의 세 가지 요인 회귀에서, 이 두 포트폴리오의 베타는 1.04와 1.06입니다.
일반적으로, 회귀에 SMB 및 HML을 추가하면 주식의 베타가 1.0으로 수렴됩니다:
낮은 베타는 1.0으로 올라가고 높은 베타는 내려갑니다.
이러한 행동은 물론 시장과 SMB 또는 HML 간의 상관관계 때문입니다.
SMB와 HML은 거의 상관관계가 없지만(-0.08), RM-RF와 SMB 및 HML 수익률 간의 상관관계는 0.32 및 -0.38입니다.
'WBS - 2024 Fall > 포트폴리오 매니지먼트' 카테고리의 다른 글
| (PF Mgmt #13) (13) 일별 데이터, 인트라데이(장중) 데이터의 분석 (0) | 2025.01.17 |
|---|---|
| (PF Mgmt#12) (12) 신용 리스크 지표 및 채무 불이행 확률의 추정 (0) | 2025.01.10 |
| (PF Mgmt #11) (11) 포트폴리오 스타일 분석 (0) | 2024.12.20 |
| (PF Mgmt #10) (10) 재무 회계의 의사결정 지원 기능과 주식 가치 평가 (0) | 2024.12.13 |
| (PF Mgmt #9) (9) 일반화된 모멘트 방법 (0) | 2024.12.06 |
| (PF Mgmt #8) (8) Fama-MacBeth형 회귀 분석 (0) | 2024.11.29 |
| (PF Mgmt #7) (7) 포트폴리오 방법을 이용한 정보 분석 (0) | 2024.11.22 |
| (PF Mgmt #6) (6) 제약 조건이 있는 포트폴리오 최적화 (0) | 2024.11.15 |



