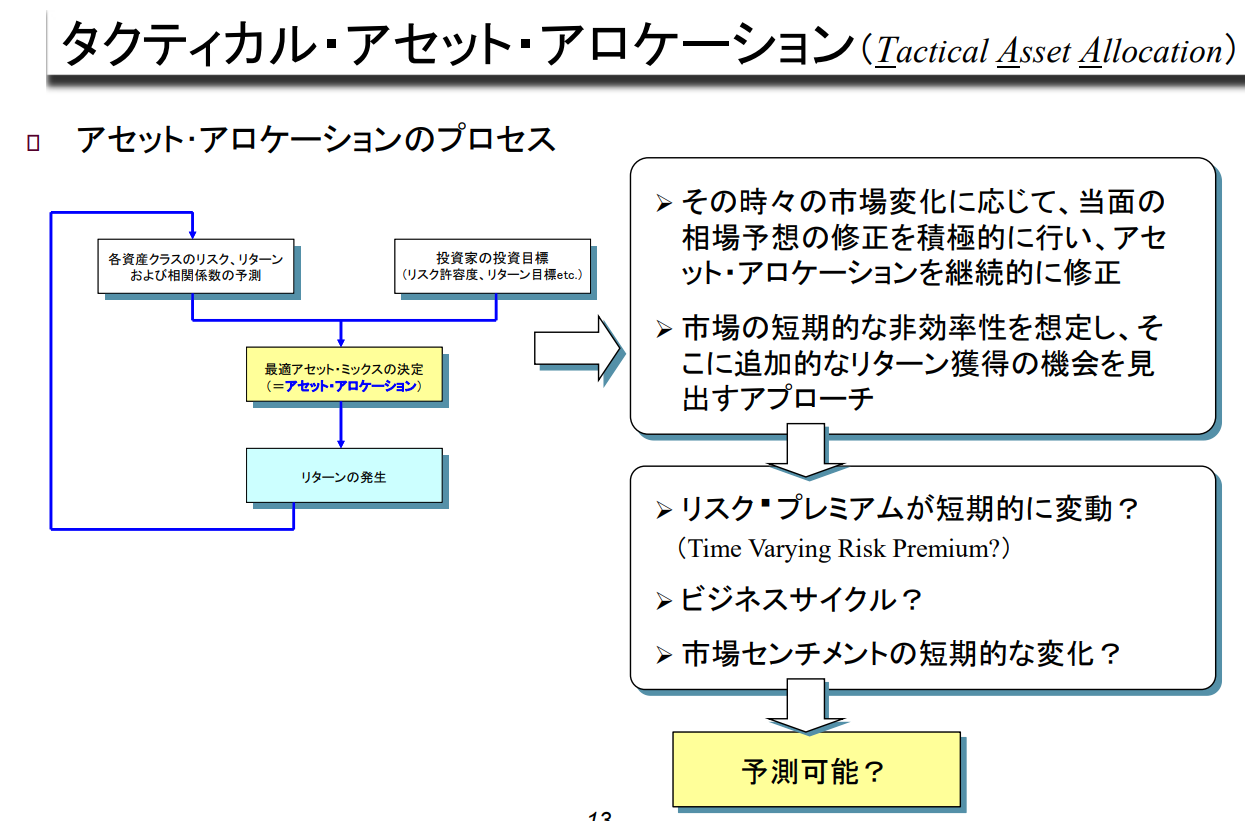
Tactical Asset Allocation

지난 번 복습 (제3회 수업)
Asset Allocation Process

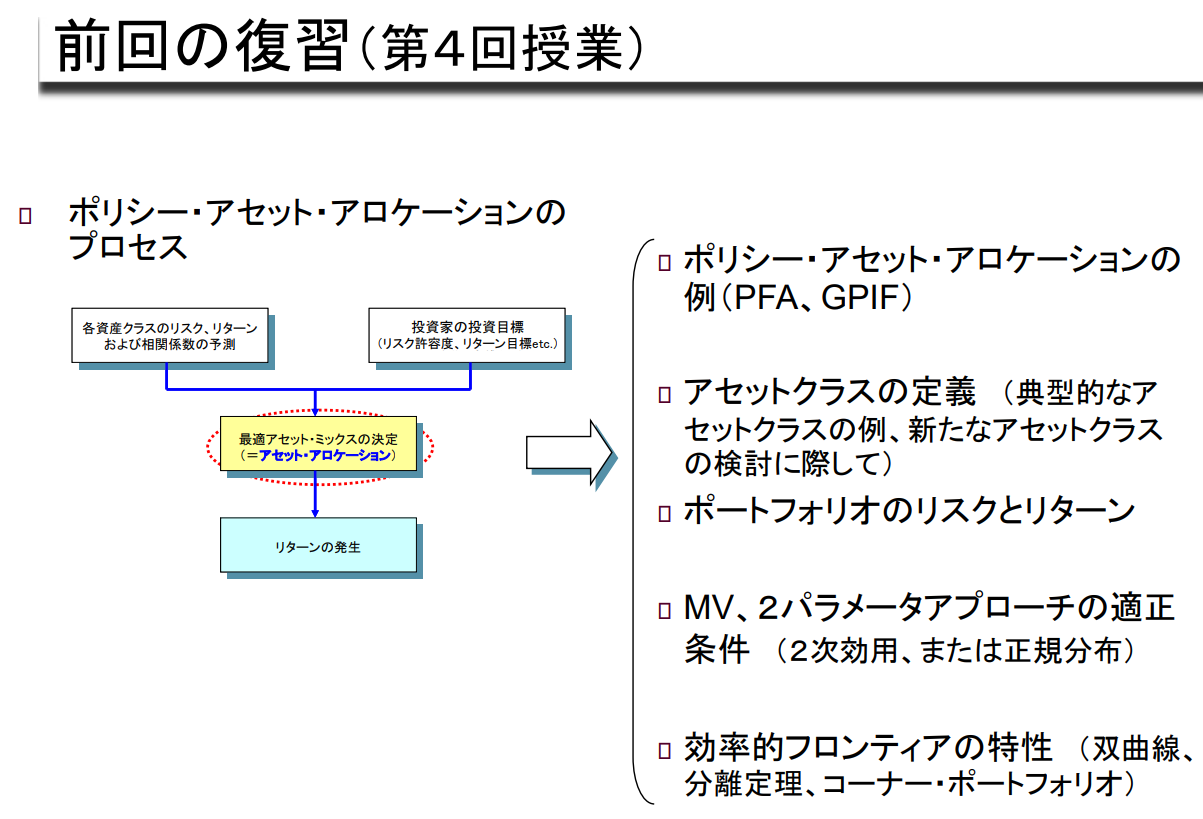
지난 번 복습 (제4회 수업)
Policy Asset Allocation Process
정책 자산배분 예시 (PFA, GPIF)
자산 클래스 정의 (전형적인 자산 클래스의 예시, 새로운 자산 클래스를 고려할 때)
포트폴리오의 위험과 수익률
MV, 2 Parameter Appoach의 적정 조건 (2차 효용, 또는 정규분포)
효율적 프런티어의 특성 (쌍곡선, 분리정리, 코너 포트폴리오)
| E(Rs) = 6% | E(Rb) = 1% |
| σs = 20% | σb = 4% |
| ρsb = 0.1 |
주식 0.4
채권 0.6
Rp = 0.4 Rs + 0.6 Rb
E(Rp) = E ( 0.4 Rs + 0.6 Rb )
= 0.4 E(Rs) + 0.6 E(Rb)
= 0.4 x 0.06 + 0.6 x 0.01 = 0.03 = 3%
| [ 0.4 0.6 ] | 6% 1% |
= 0.4 x 6% + 0.6 x 1% = 3%
| 1 x 3 | 3 x 2 |
| [ x1 x2 x3 ] | y11 y12 [ y21 y22 ] y31 y32 |
| 1 x 2 = [ x1 y11 + x2 y21 + x3 y31 x1 y12 + x2 y22 + x3 y32 ] |
|
| 3 x 1 x1 [ x2 ]T x3 |
= 전치 |
1 x 3 [ x1 x2 x3 ] |
| σs = 20% |
| σb = 4% |
| ρsb = 0.1 = cov ( Rs, Rb ) / σs σb |
| cov ( Rs, Rb ) σs σb |
| cov ( Rs, Rb ) = E [ { Rs - E(Rs) } { Rb - E(Rb) } ] |
| 분산공분산 Σ = |
σs^2 | ρsb σs σb |
| ρsb σs σb | σb^2 |
| 일본주식 | 엔화채권 | 외국주식 | 외국채권 | ||
| Σ = | 일본주식 | σ11 | σ12 | σ13 | σ14 |
| 엔화채권 | σ21 | σ22 | σ23 | σ24 | |
| 외국주식 | σ31 | σ32 | σ33 | σ34 | |
| 외국채권 | σ41 | σ42 | σ43 | σ44 |
σ외국주식 = √σ33
σ엔화채권 = √σ22
ρ외주엔채 = σ32 / √σ33 √σ22
분산
σx^2 = E [ { x - E(x) }^2 ]
표준편차
σx = √σx^2



2 자산 Portfolio의 기대 Return, Risk (1)
자산의 수익률 분포(R1, R2)가 다음과 같은 다차원 정규분포를 따른다고 가정한다.
R1
R2 ~ N( µ , Σ )
자산가격 w1, 자산가격 w2만 보유할 경우의 기대수익률 분포 Rp는 다음과 같다.



2 자산 포트폴리오의 기대수익률과 위험(2)
Rp = w1 Rs + w2 Rb
σp^2 = E { Rp - E(Rp) }^2
= E [ w1 Rs + w2 Rb - E { w1 Rs + w2 Rb } ]^2
= E [ w1 { Rs - E(Rs) } + w2 { Rs - E(Rb) } ] ^2
= w1^2 σ
s^2 + 2 w1 w2 σsb + w2^2 σb^2
Rp = w1 R1 + w2 R2 + w3 R3 + w4 R4
σp^2 = w1^2 σ1^2 + w2^2 σ2^2 + w3^2 σ3^2 + w4^2 σ4^2
= 2 w1 w2 σ12 + 2 w1 w3 σ13 + 2 w1 w4 σ14 + 2 w2 w3 σ23 + 2 w2 w4 σ24 + 2 w3 w4 σ34
| 1 x 2 | 2 x 2 | 2 x 1 | ||
| σp^2 | = | [ w1 w2 ] | σ11 σ12 σ21 σ22 |
w1 w2 |
| 1 x 2 | 2 x 1 | |||
| = | [ w1 σ11 + w2 σ21 w1 σ12 + w2 σ22 ] | w1 w2 |
||
| = | w1^2 σ11 + w1 w2 σ21 + w1 w2 σ12 + w2^2 σ22 | |||
| = | w1^2 σ11 + 2 w1 w2 σ21 + w2^2 σ22 | |||

2 자산 Portfolio의 기대 Return Risk (2)

σp^2 = w' Σ w
= sqrt ( σp^2 )
= mmult (transpose(w) , mmult ( Σ , w ) )
※ 엑셀에서 행렬 곱하기:
= mmult ( x 범위, y 범위 ) Ctrl+Shift+Enter
2 자산 Portfolio의 기대 Return Risk (3)

다자산 포트폴리오의 기대수익률과 리스크

다자산 포트폴리오의 기대수익률과 리스크(2)

연습04-1 : 최적 Portfolio의 산출

연습04-1 : 최적 Portfolio의 산출(계속)

2 Parameter Approach
2 Parameter Approach이란?
- 평균-분산 2 Parameter로 Portfolio를 선정하는 방법
- Markowitz(1952) 이후 학계 및 실무계에서 주류로
2 Parameter 접근법이 적합한 조건
- 투자자의 기대효용함수가 2차효용
또는
- 증권의 수익률 분포가 (다차원) 정규분포
특히 증권의 수익률 분포가 (다차원) 정규분포이고 투자자의 기대효용함수가 승수효용인 경우,
Max E [ U ( Wr ) ] 은 Max E [ ( µp - (r/2)σp^2 ) ] 와 같이 다시 쓸 수 있다.

효율적 Frontier 특성 (비부정적 제약이 없는 경우)
이상을 정리하면, 비부정 제약이 없는 경우 분산 최소 Frontier의 특성은 다음과 같다.
- Frontier 상의 임의의 Portfolio는 2개의 Portfolio g, h의 선형 합으로 표현 가능
→ Frontier 상의 임의의 2 Portfolio로 Frontier 상의 모든 Portfolio를 표현할 수 있다.
분리정리 (Two Fund Separation Theorem)
분산 최소 Frontier는 평균/표준편차 평면에서 쌍곡선을 그린다.


Tactical Asset Allocation
| 시장 변화에 따라 당장의 시장 전망을 적극적으로 수정하고, 자산 배분을 지속적으로 수정하는 접근 방식 시장의 단기적 비효율성을 가정하고, 이를 통해 추가 수익 창출의 기회를 찾는 접근 방식 ↓ |
| 리스크 프리미엄이 단기적으로 변동? (Time Varying Risk Premium?) 비즈니스 사이클? 시장 심리의 단기적 변화? ↓ |
| 예측가능? |
닛케이 평균 2023년 10월 말 예상?

2023년 10월말 환율(JPY/USD) 예상은?

완벽히 예측할 수 있는 경우의 TAA의 가능성

단기 수익률 예측 접근법 예시
- Fundamental Approach
- 거시경제지표(GDP 성장률, 산업생산지수, 통화량 등)와 시장 데이터(금리, 기간 스프레드, 수익률 스프레드, 디폴트 스프레드 등)를 이용하여 투자대상 자산의 미래 수익률 예측
- 예측 Horizon이 1~6개월 정도인 경우 폭넓게 활용
- Tactical Approach
- 투자 대상 자산의 과거 가격 변화에 주목하여 미래 수익률 예측
- 예측 호라이즌이 1일~1개월 등 비교적 단기간인 경우에 폭넓게 활용

회귀분석을 통한 수익률 예측
동시 결정형 vs. 예측형
- 동시 결정형:
미래 환율이나 금리 시나리오를 통해 미래 주식 수익률을 예측하는 경우.
- 예측형:
현재 관측 가능한 환율, 금리 등의 데이터로 미래 주식 수익률을 예측하는 경우.

단기 수익률의 예측 가능성

거시경제 변수와의 관계
Granger의 인과관계 분석 사례 (篠崎・岩澤(1994))
Granger의 인과관계 분석이란?
를 사용하여 다음과 같은 귀무가설을 F검정

자산운용 분야 기술의 진화
| 분석 기술 고도화 | 분석 데이터 다양화 |
| 고속 연산(클라우드 컴퓨팅, GPU 컴퓨팅) 머신러닝 딥러닝 자연어 학습 생성형 데이터(문서, 음성, 이미지, 영상 등) |
비구조화 데이터 (문서, 음성, 이미지 등) 비전통적 데이터 (시장 고빈도 거래 데이터, 인터넷 정보, 고객 행동 데이터, POS 데이터, 소셜 미디어 등) |

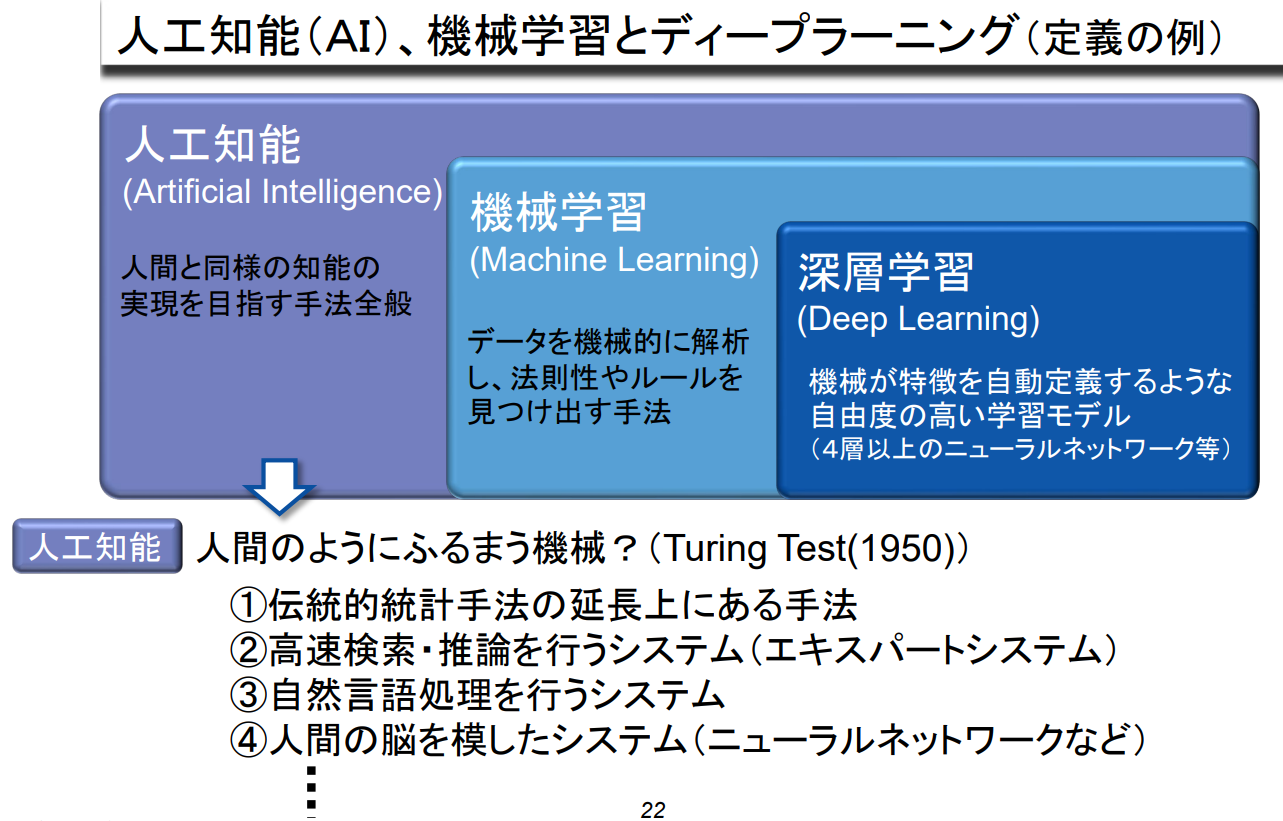
인공지능(검색엔진), 머신러닝과 딥러닝(정의 예시)
| 인공지능(Artificial Intelligence) 인간과 같은 지능을 구현하기 위한 기법 전반. |
| 머신러닝(Machine Learning) 데이터를 기계적으로 분석하여 법칙이나 규칙을 찾아내는 기법 |
| 딥 러닝(Deep Learning) 기계가 특징을 자동 정의하는 자유도가 높은 학습 모델(예: 5층 이상의 신경망 등) |
의사결정나무(Decision Tree)란?
의사결정나무는 나무 구조를 이용해 데이터를 분석하는 방법이다.
머신러닝 알고리즘 중 하나다.
의사결정나무를 시각화하여 모델의 판단 기준을 한눈에 파악할 수 있는 것이 특징.

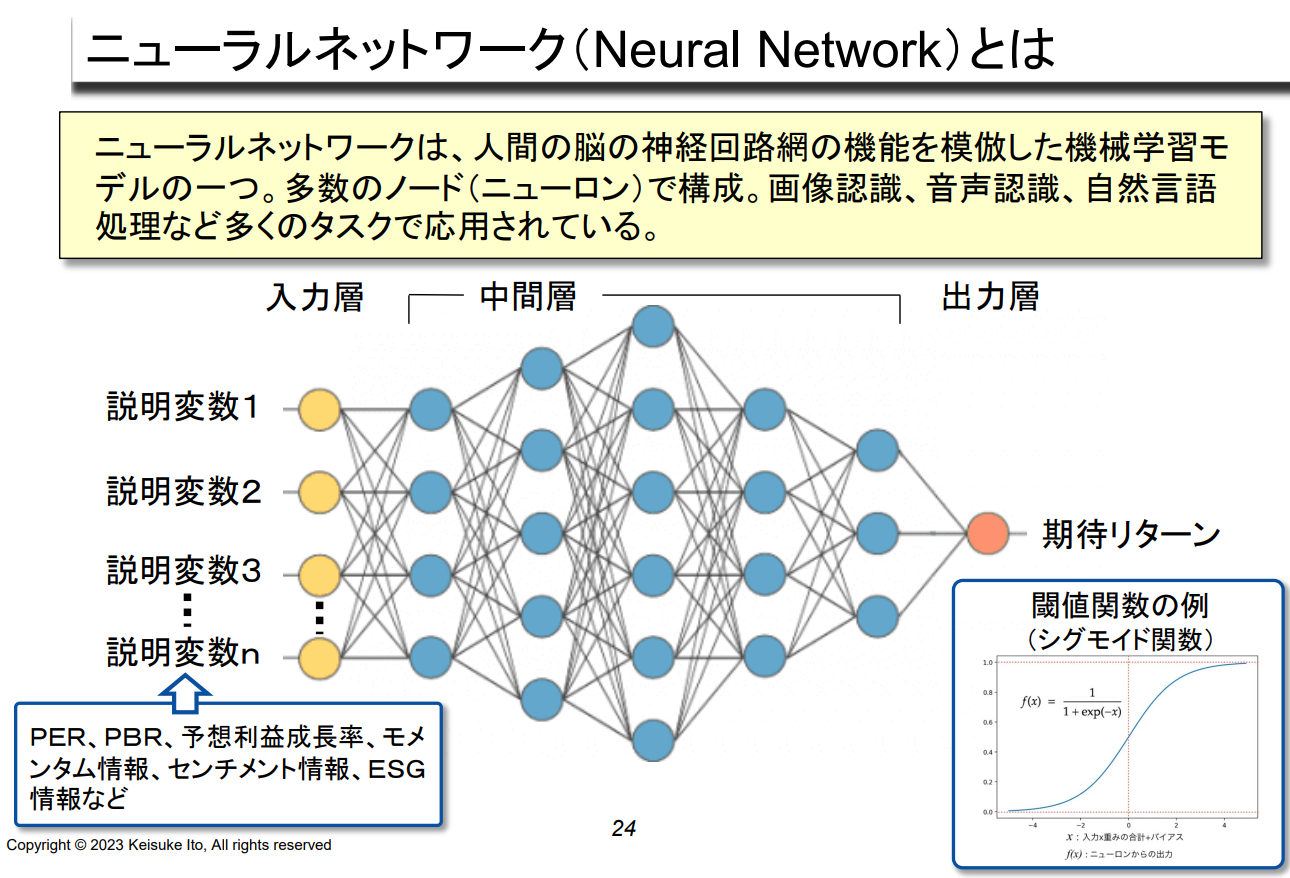
신경망(Neural Network)이란?
신경망은 인간 뇌의 신경망 기능을 모방한 기계학습 모델 중 하나다.
다수의 노드(뉴런)로 구성된다.
이미지 인식, 음성 인식, 자연어 처리 등 많은 작업에 적용되고 있다.
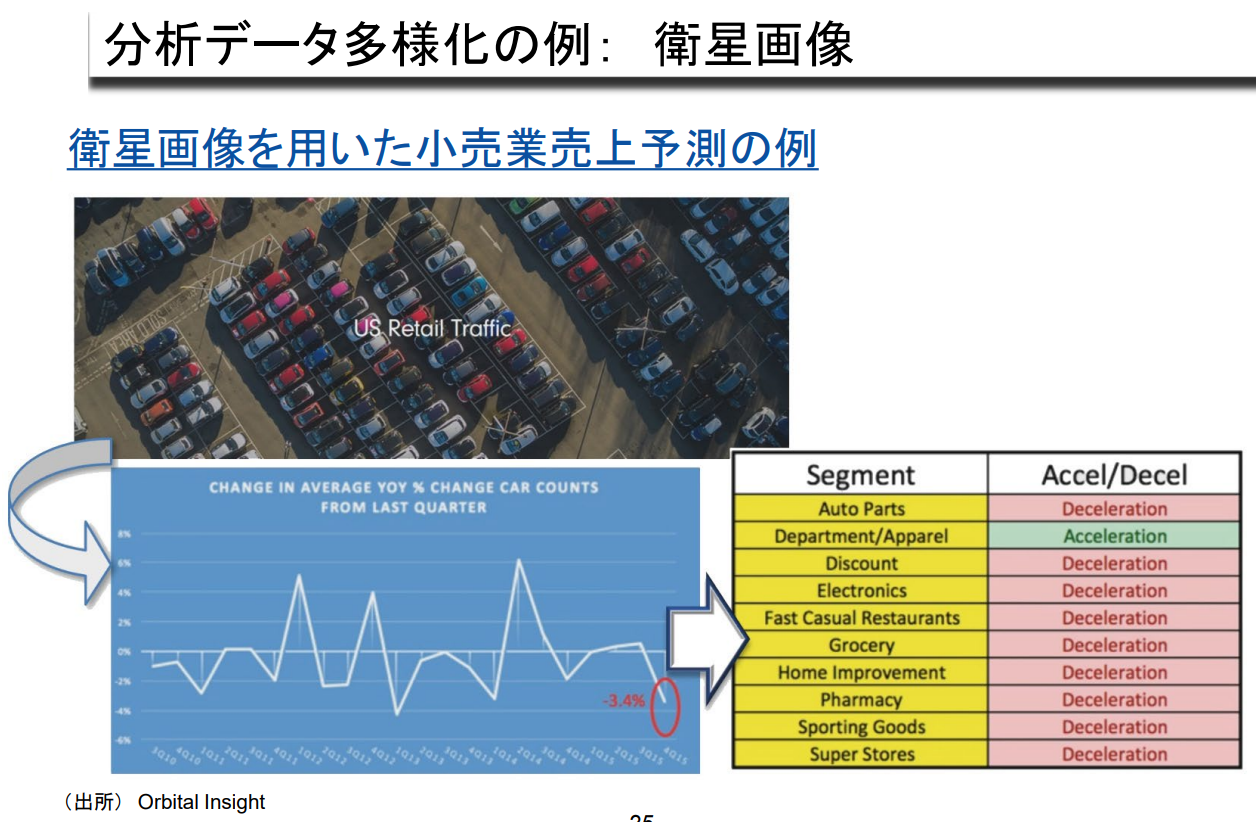
분석 데이터 다양화 사례: 위성 이미지
위성사진을 이용한 소매업 매출 예측의 예
2. 블랙리터만형 최적화

TAA에 대한 실무적 과제의 예시
기대수익률 설정에 따라 극단적인 배분이 쉽게 계산될 수 있다?

균형수익률이란?
- 모든 투자자는 다음과 같은 효용을 극대화하는 포트폴리오를 선택한다고 가정한다.
Max U = μp - (λ/2)σp^2 = w'pμ - (λ/2)w'pΣwp
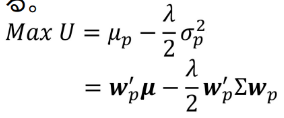
- 최적 포트폴리오 wp는 아래의 1층 조건(First Order Condition)을 만족해야 한다.
FOC: əU / əw = μ - λΣwp

- 이 결과, 모든 투자자가 보유한 포트폴리오가 시장 포트폴리오인 wp*라고 가정하면,
이 포트폴리오가 최적해가 되기 위한 기대수익률 벡터 μ*는 다음과 같이 역산된다.
이 μ*를 균형수익률이라고 한다.
μ* = λΣwp*







Black-Litterman 유형 최적화란 (혼합추정)


시나리오 표현 예시
시나리오 1: 국내 주식의 수익률은 5.0%이다.
시나리오 2: 국내 주식의 수익률은 해외 주식보다 1.0% 높다.
시나리오 3: 국내 채권 수익률은 해외 채권 수익률보다 0.5% 낮다.
| Scenario 행렬 [P] | Scenario Return [Q] | |||||
| 국내채권 | 국내주식 | 외국채권 | 외국주식 | |||
| 1 | 0 | 1 | 0 | 0 | 5.0% | |
| 2 | 0 | 1 | 0 | -1 | 1.0% | |
| 3 | 1 | 0 | -1 | - | -0.5% | |
| 국내채권 0 0 1 |
국내주식 1 1 0 |
외국채권 0 0 -1 |
외국주식 0 -1 0 |
E(R국내채권) E(R국내주식) E(R외국채권) E(R외국주식) |
5% 1% -0.5% |
E(R국내주식) = 5%
E(R국내주식) - E(R외국주식) = 1%
E(R국내채권) - E(R외국채권) = -0.5%


Black-Litterman형 최적화의 특징
기본 포트폴리오를 미리 설정
-- 시세를 입력하지 않는 경우 기본 포트폴리오가 최적.
자신 있는 시세관만 입력하면 된다.
자산 간 상대적 관계 입력 가능

3. 액티브 운영의 기본 법칙

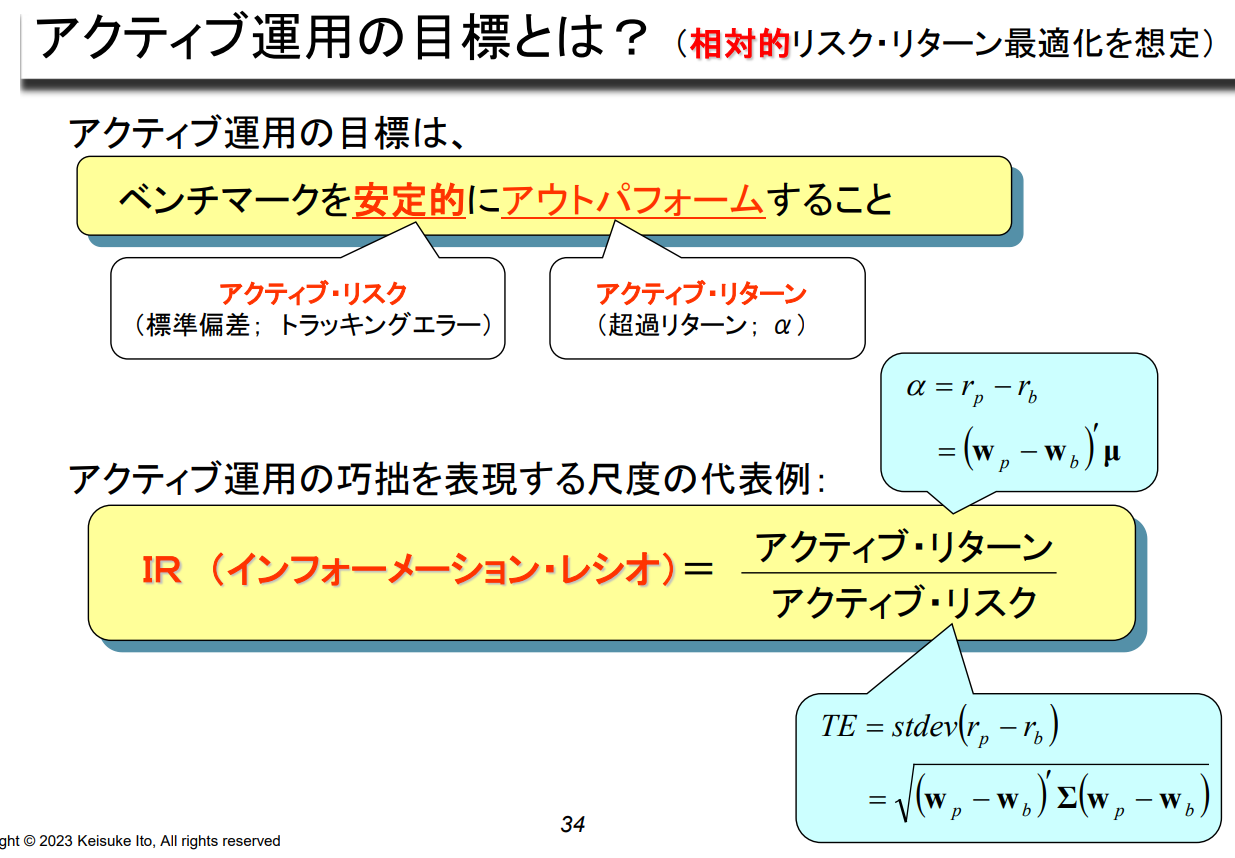
액티브 운용의 목표란? (상대적 위험-수익률 최적화를 가정)
액티브 운용의 목표,
벤치마크를 안정적으로 Out Perform하는 것입니다.
Active Risk (표준편차, 추적 오류)
Active Return (초과수익률, α)
액티브 운용의 숙련도를 표현하는 척도의 대표적인 예입니다:
IR (Information Ratio) = Active Return / Active Risk
액티브 운용의 기본 법칙이란?
정보 비율(Information Ratio)은 다음과 같은 요소에 의해 결정된다 (= Fundamental Law of Active Management).
① 개별 종목의 예측 정확도 (=IC; Information Coefficient; 정보계수)
② 포트폴리오의 효율성 (=TC; Transfer Coefficient; 전달계수)
③ 베팅 수 (=Breadth; 투자 대상 종목 수)
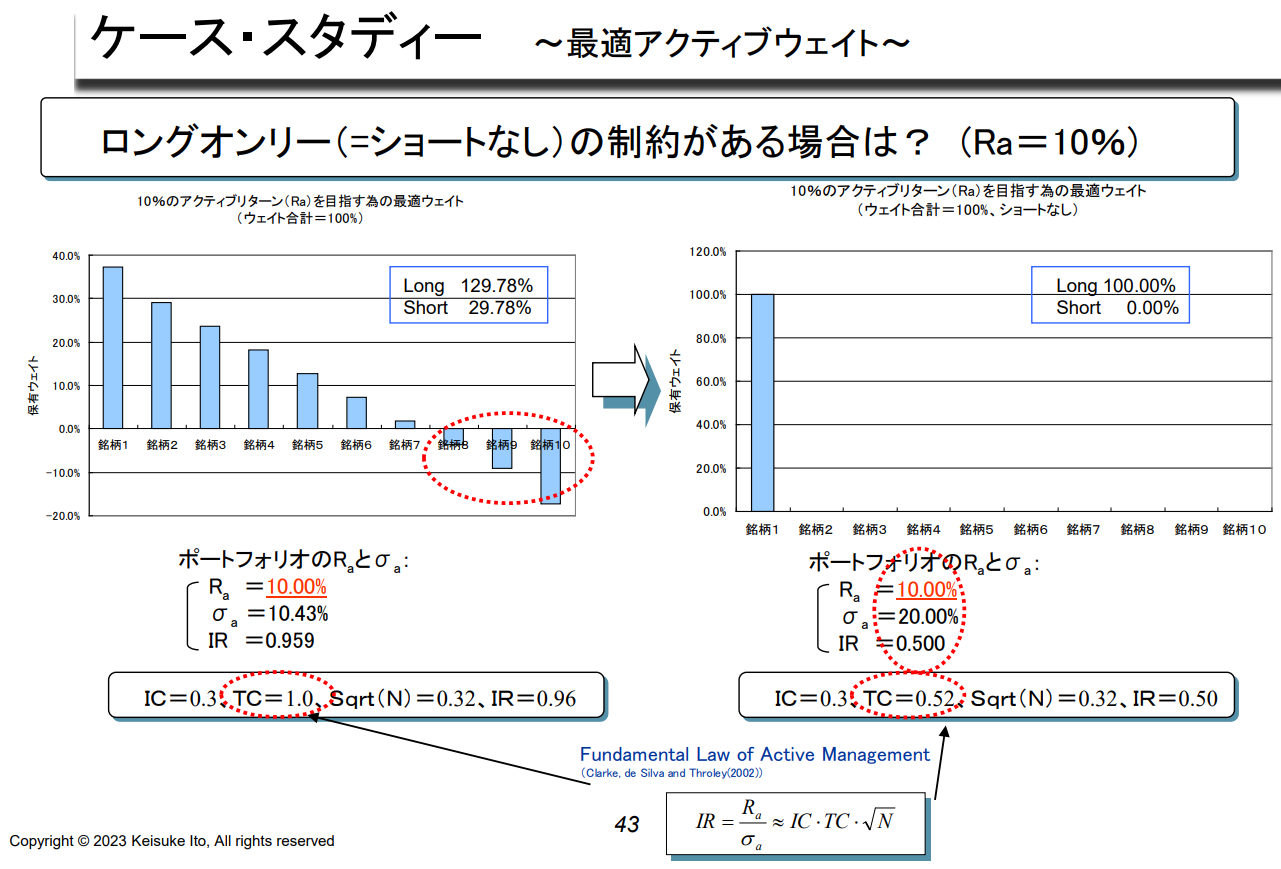
Fundamental Law of Active Management (Clarke, de Silva and Throley(2002))

| IC = 0.1 ~ 0.3 | 0.2 |
| TC = 0.2 ~ 0.4 | 0.3 |
| √N = √9 | 3 |
| IR = 0.18 | |

IC(Information Coefficient)란?
IC(Information Coefficient; 정보계수)는 개별 종목의 예측 정확도를 나타내는 척도이다.
- 개별 종목의 세계에서는 장기적으로 볼 때, 0.05~0.1이면 우수한 예측이라고 한다.

TC(Transfer Coefficient)란?
TC(Transfer Coefficient, 전달계수)는 포트폴리오의 효율성을 나타내는 척도이다.
- 전혀 제약이 없는 경우, 최적 포트폴리오는 0.5가 된다.
- 실제로는 비음의 제약, 회전율 제약 등으로 인해 전이계수는 0.1~0.5 정도로?

사례 연구 - 종목별 수익률 전망

사례 연구 - 최적 액티브 웨이트
앞의 가정 하에 가장 안정적으로 더 높은 액티브 수익률을 노릴 수 있는 방법은?
액티브 웨이트를 같은 비율로 부풀려 액티브 리턴-액티브 리스크 확대

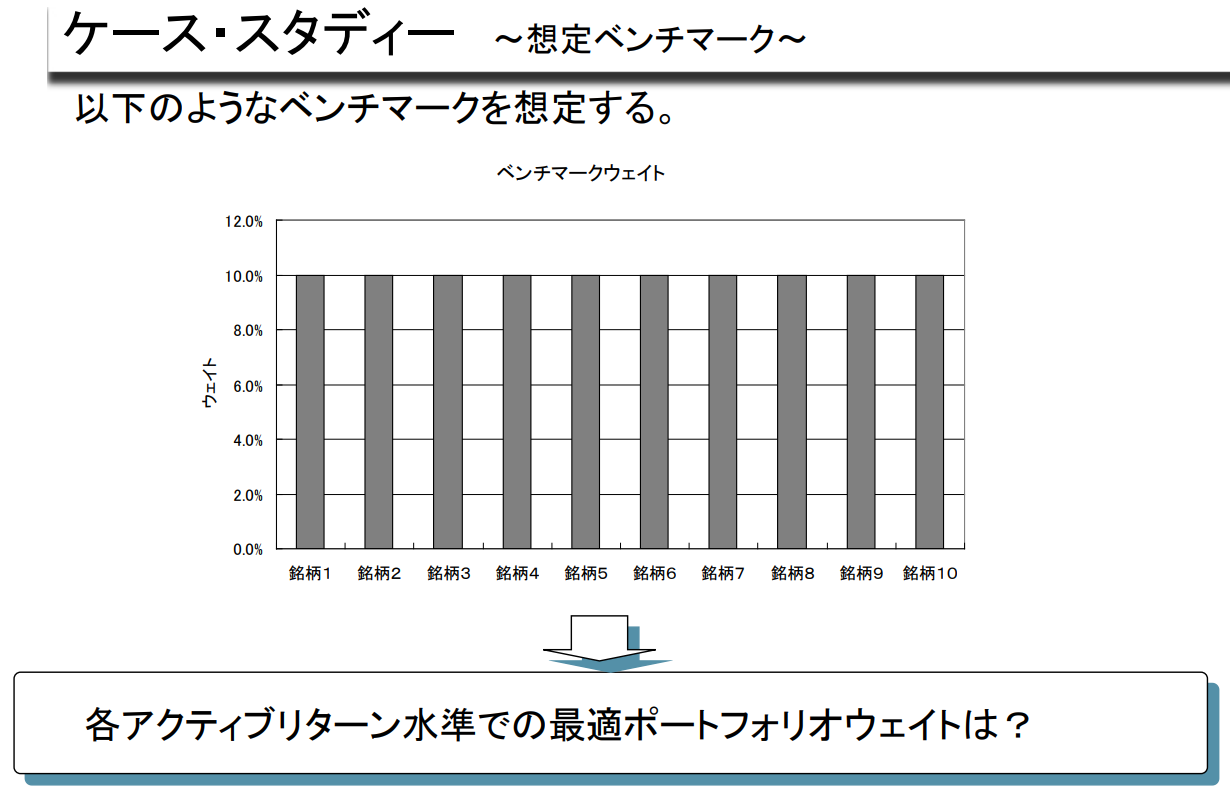
사례 연구 - 가정 벤치마킹
다음과 같은 벤치마크를 가정한다.
각 액티브 수익률 수준에서 최적의 포트폴리오 비중은?


'WBS - 2023 Fall > 자산배분' 카테고리의 다른 글
| [자산배분 #13-14] (0) | 2023.11.25 |
|---|---|
| (자산배분 #11-12) 대체투자 및 해외 분산투자 | 자산 배분에 대한 성과 평가 (0) | 2023.11.18 |
| (자산배분 #9-10) Strategic Asset Allocation | 개인 투자가의 Asset Allocation | 다기간 Asset Allocation의 실제 (0) | 2023.10.28 |
| (자산배분 #7-8) Dynamic Asset Allocation | Allocation 최적화를 위한 노력 (0) | 2023.10.28 |
| (자산배분 #3-4) 투자방침의 책정 | Policy Asset Allocation (0) | 2023.10.14 |
| (자산배분 #1-2) Asset Allocation의 중요성과 그 Framework (0) | 2023.10.07 |



