Dynamic Asset Allocation

Dynamic Asset Allocation
Asset Allocation의 Process
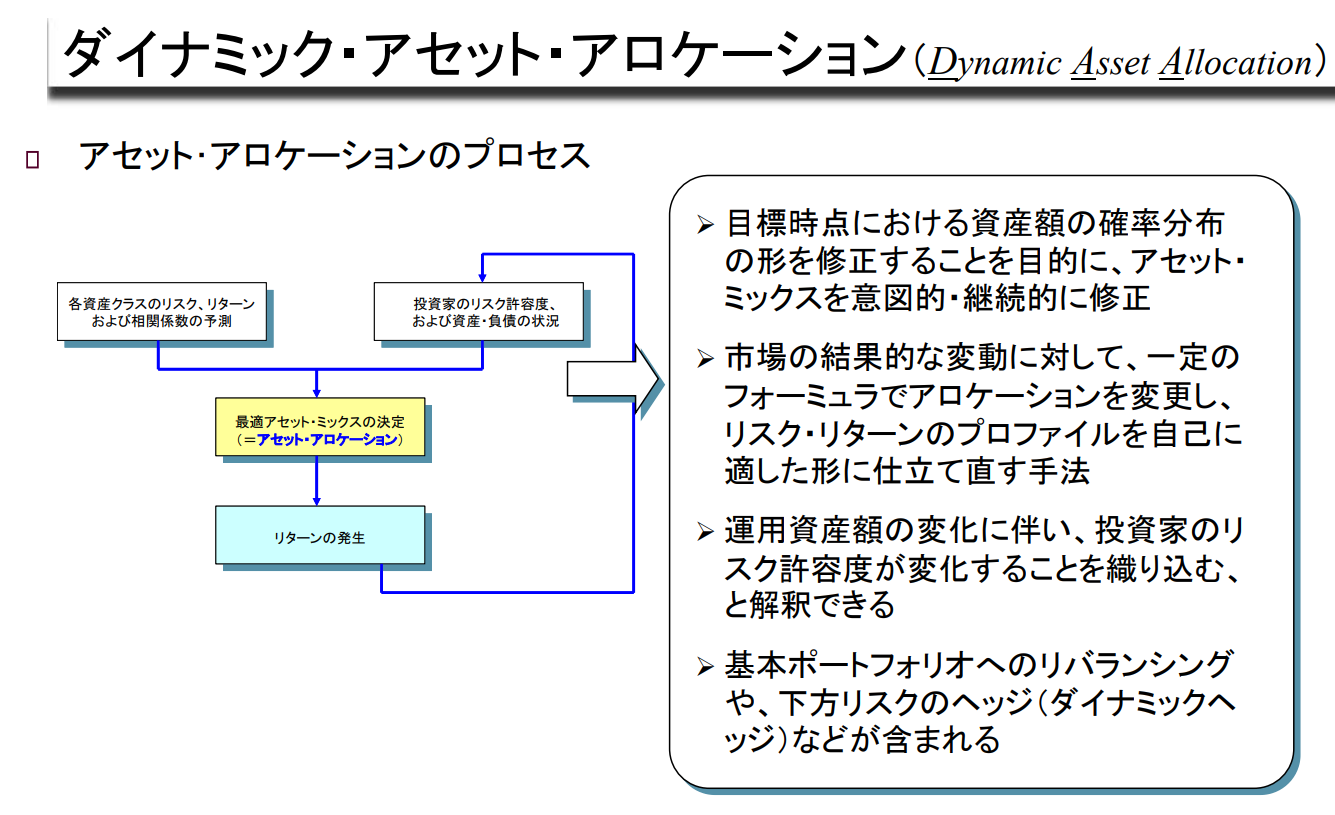
➢ 목표 시점의 자산 금액의 확률분포 형태를 수정하기 위해 의도적, 지속적으로 자산믹스를 수정하는 방법
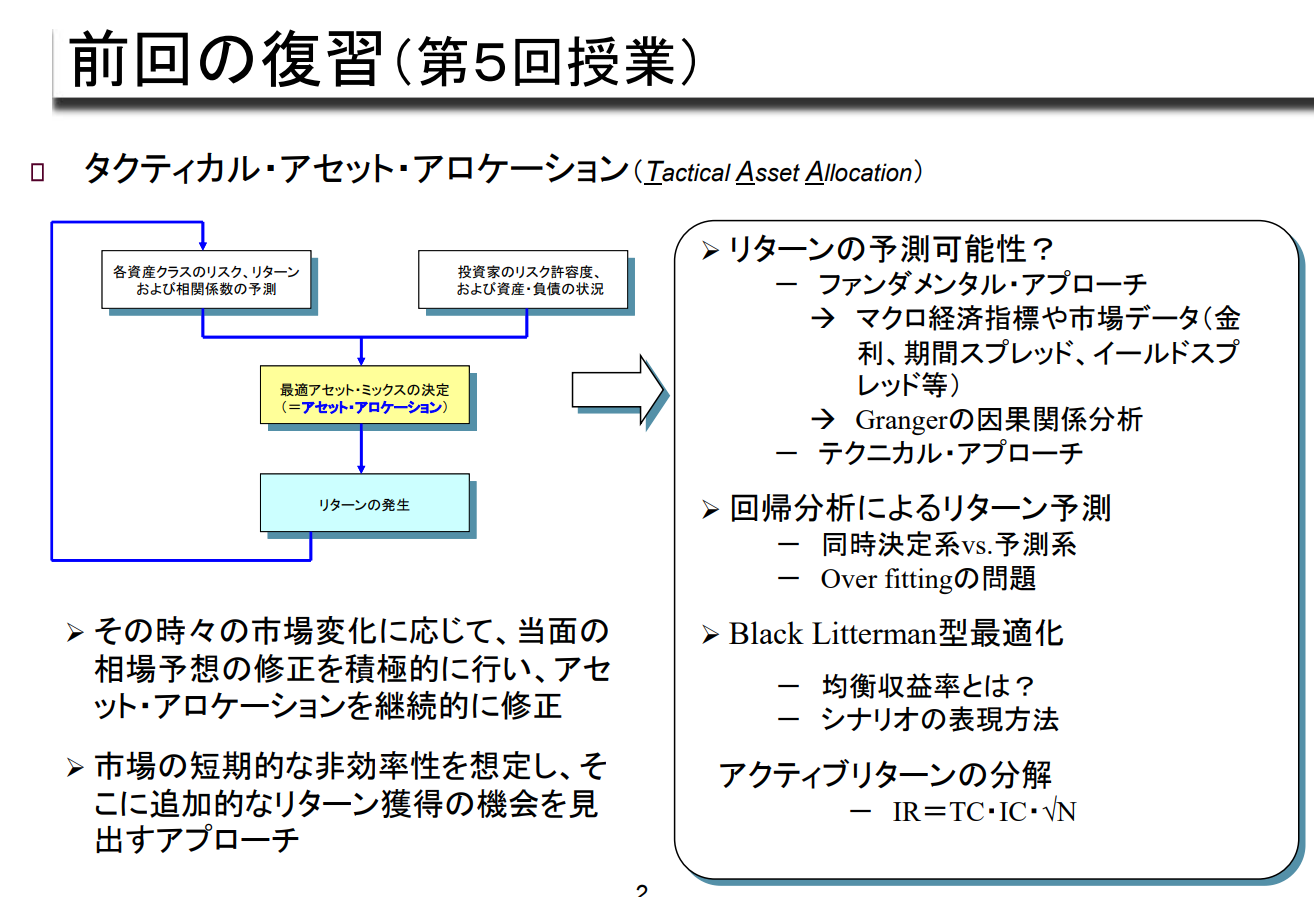
➢ 시장의 결과적 변동에 대해 일정한 공식에 따라 자산배분을 변경하여
위험- 수익률 프로파일을 자신에게 적합한 형태로 재구성하는 기법
➢ 운용자산 규모의 변화에 따라 투자자의 위험 허용 범위가 변화하는 것을 반영하는 것으로 해석할 수 있다.
➢ 기본 포트폴리오에 대한 리밸런싱, 하방위험 헤지(Dynamic Hedge) 등이 포함됨.
볼록 전략과 오목 전략
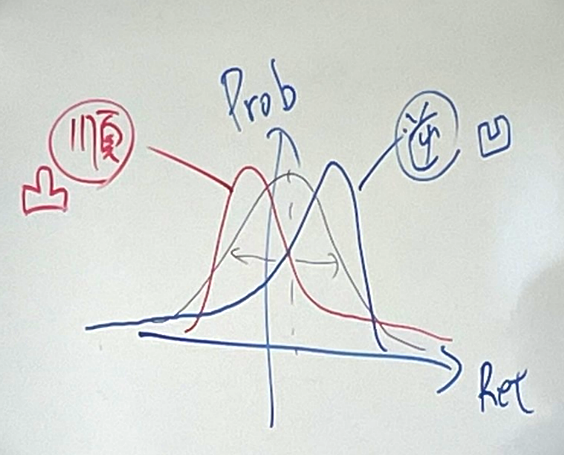
DAA 중 순방향적인 공식을 따르는 것을 볼록 전략, 역방향적인 공식을 따르는 것을 오목 전략이라고 한다.
X: 만기 T 시점의 위험자산 가격
Y: 각 전략으로 매매를 반복했을 때 T 시점의 포트폴리오 가치
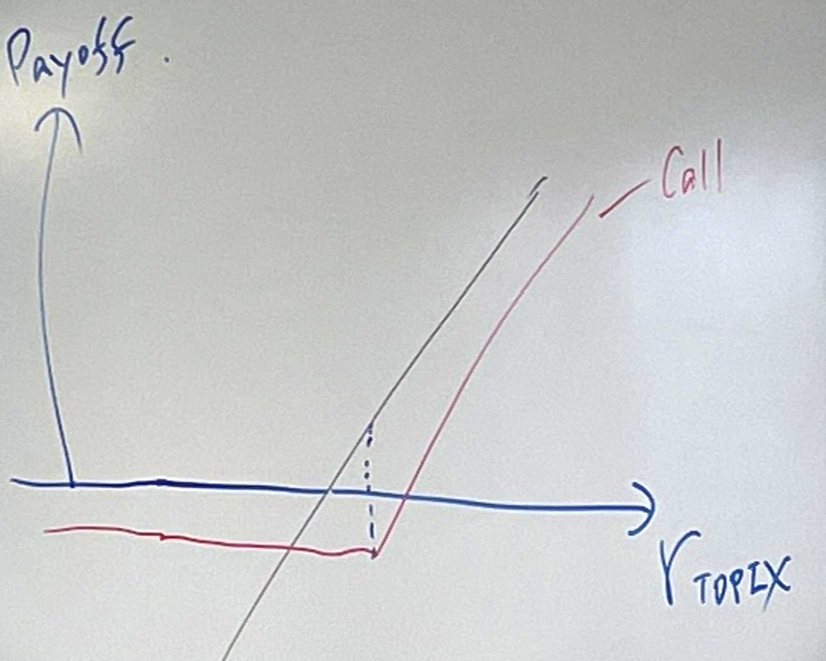
① Buy & Hold 전략
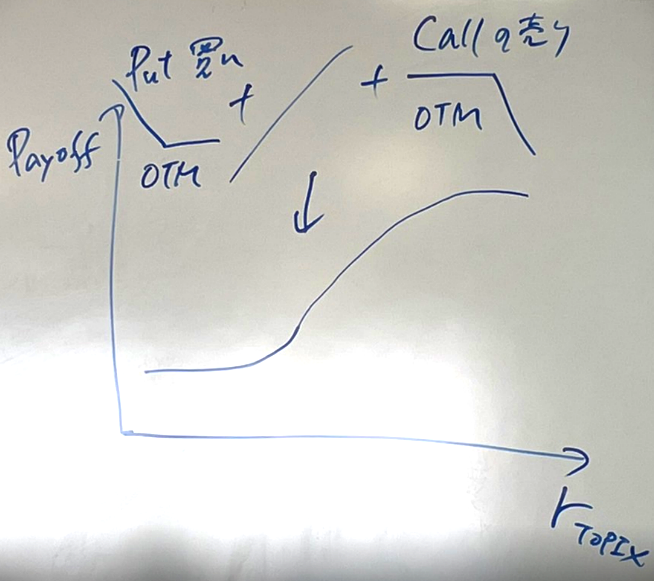
② 볼록 전략 (순매수 전략) (CPPI, OBPI 등 다이내믹 헤지 전략) - Call Option의 Buy
→ 트렌드 시세에서 유리
③ 오목한 전략 (역방향 전략) (정책적 자산믹스에 대한 정기적인 리밸런싱 등) - Put Option의 Sell
→ 박스권 장세에서 유리

볼록 전략의 종류(順張り戦略)
OBPI (Option Based Portfolio Insurance)
- 옵션의 보상을 동적으로 재현하는 방법. 델타 헤지가 기본
CPPI (Constant Proportion Portfolio Insurance)
- 바닥까지의 거리(여유도)의 일정 배만큼 위험자산을 보유하는 방법.
TIPP (Time Invariant Portfolio Protection)
- CPPI를 확장한 형태. 래칫업형 플로어도 포함된다.


옵션을 복제한다는 것은, 옵션 계약의 페이오프 구조를 다른 금융 상품을 이용하여 재현하는 것을 말합니다.
이는 주로 동적 헤징 또는 델타 헤징이라는 기법을 사용하여 이루어집니다.
예를 들어, OBPI (Option Based Portfolio Insurance) 전략에서는 콜 옵션의 페이오프를 동적으로 재현합니다.
이는 주식과 위험 없는 자산 (예: 국채)을 적절하게 조합하여,
주식 가격이 상승하면 이익을 얻고, 주식 가격이 하락하면 손실을 제한하는 페이오프 구조를 만드는 것입니다.
델타 헤징은 이 과정에서 중요한 역할을 합니다.
델타는 옵션 가격이 기초 자산 가격 변동에 얼마나 민감하게 반응하는지를 나타내는 값입니다.
델타 헤징은 이 델타를 이용하여,
옵션의 페이오프와 동일한 페이오프를 가지도록 주식의 매매를 조정하는 것입니다.
예를 들어, 델타가 0.5인 콜 옵션을 복제하려면, 주식을 0.5개 단위로 매매하면 됩니다.
즉, 주식 가격이 $1 상승하면 옵션 가격은 $0.5 상승하므로,
주식을 0.5개 매수하면 옵션의 페이오프를 복제할 수 있습니다.
이렇게 옵션을 복제하면, 옵션의 페이오프 구조를 이용하여 포트폴리오를 보호하면서도,
주식 시장의 상승 트렌드에서 이익을 얻을 수 있습니다. 이는 볼록 전략의 핵심 원리입니다.
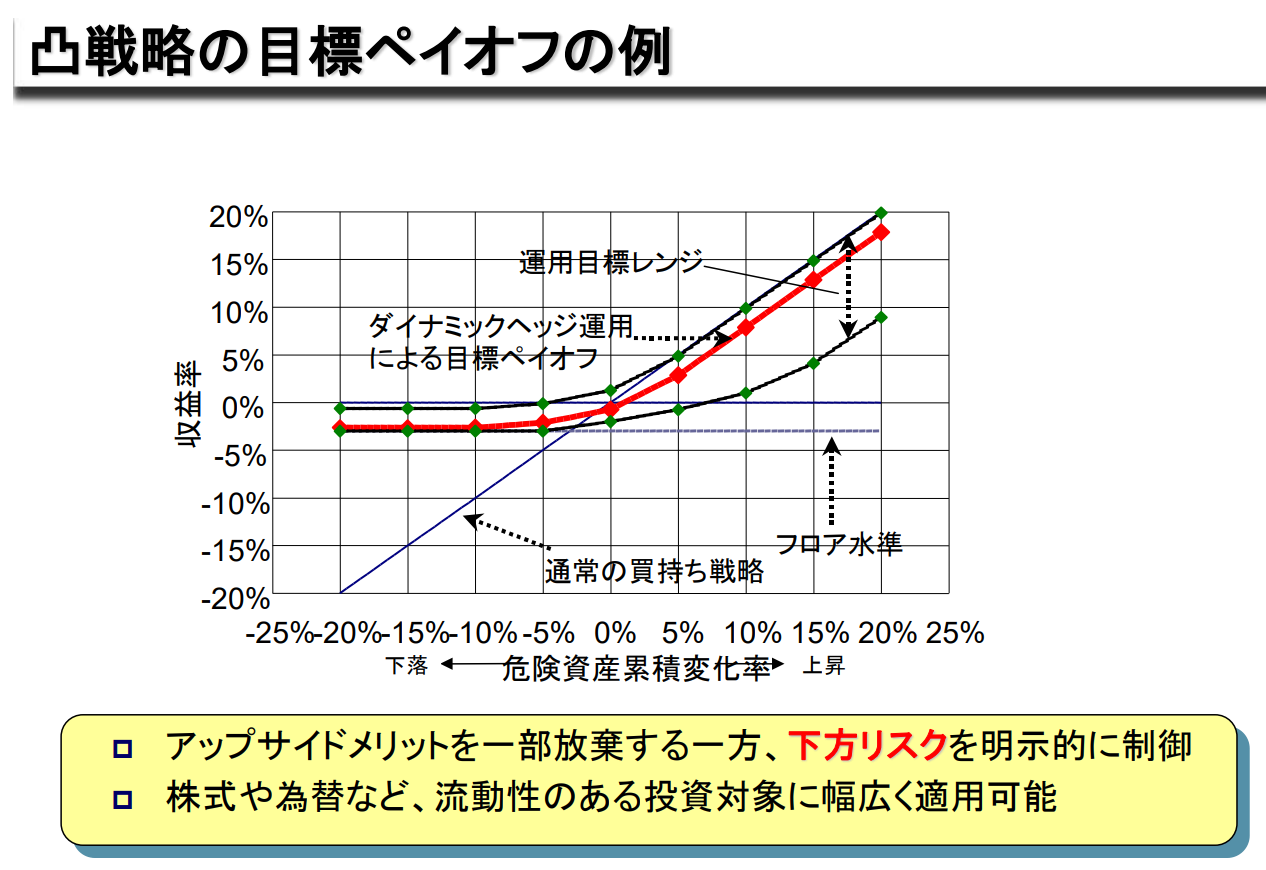
볼록 전략의 목표 보상 사례
Upside Merit을 일부 포기하는 대신 하방 위험을 명시적으로 제어
주식, 외환 등 유동성 있는 투자 대상에 광범위하게 적용 가능
볼록 전략의 효과
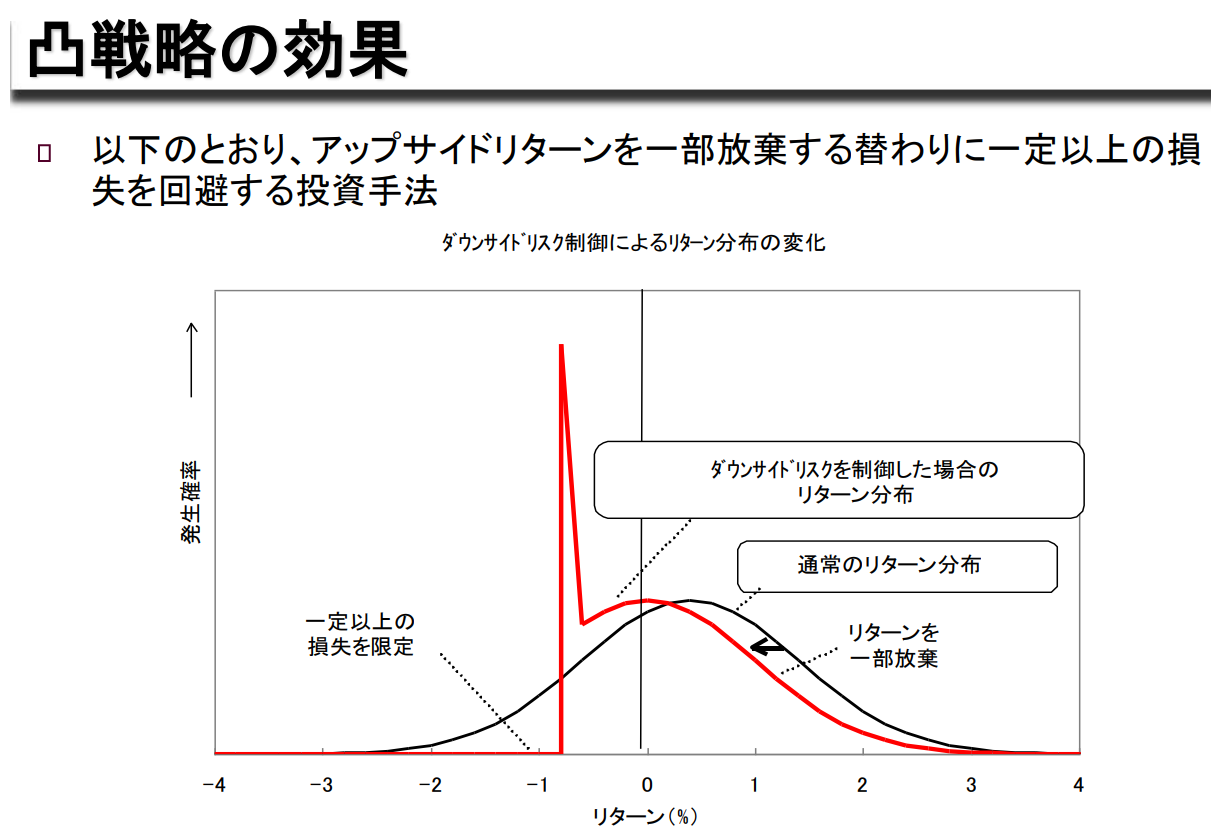
아래와 같이 Upside Return을 일부 포기하는 대신 일정 수준 이상의 손실을 회피하는 투자 방식
Downside Risk 억제에 의한 Return 분포의 변화
OBPI(Option Based Portfolio Insurance)
옵션의 델타 헤지에 해당
- 배당이 없는 주식의 경우, European Put Option의 가격은 Black-Scholes에 의해
P = Xe^-rT N(-d2) - S0 N (-d1)
단,

CPPI(Constant Proportional Protfolio Insurance)
Floor로부터의 거리에 주목 (Wealth, Floor, A 투자액)
At = m ( Wt - Ft )
Ft = F0 e^rt (연속복리)
Ft = F0 x ( 1 + r )^t
→ 만기 시 Payoff : Wt = Ft + ( W0 - F0 ) ( St / S0 )^m e^(1-m)(r+(σ^2/2)m)T
특정 보상의 재현을 목표로 하는 것이 아니라 하방 위험에 초점을 맞춘 기법
TIPP에서는 Floor를 Ratchet Up하는 개념도 도입

"Floor"는 CPPI (Constant Proportional Portfolio Insurance) 전략에서 사용되는 용어로,
포트폴리오 가치의 최소 보장 금액을 의미합니다.
이는 투자자가 손실을 감수할 수 있는 최대 범위로,
이 금액 이하로 포트폴리오 가치가 떨어지지 않도록 보장하는 역할을 합니다.
CPPI 전략에서는 투자자의 자산 (Wt)과 Floor (Ft) 사이의 거리에 따라
위험 자산에 투자할 금액 (At)을 조정합니다.
만약 포트폴리오 가치가 Floor에 가까워지면, 위험 자산에 대한 투자를 줄여 손실을 제한하고,
반대로 포트폴리오 가치가 Floor에서 멀어지면 위험 자산에 대한 투자를 늘려 이익을 증대시킵니다.
Floor는 일반적으로 고정된 값이지만,
때때로 "Ratchet Up"이라는 기법을 사용하여 Floor를 상향 조정하기도 합니다.
이는 포트폴리오 가치가 상승하면 Floor를 그에 맞춰 높여,
새로운 수준에서의 손실을 제한하는 방법입니다.
이러한 전략은 시장 상황이 긍정적일 때 투자자의 이익을 더욱 증대시키는 데 도움이 됩니다.

옵션 전략과의 비교
옵션 vs. OBPI?
옵션 vs. CPPI?
Portfolio Insurance는 정말 '보험'인가?

다이내믹 헤지(OBPI, CPPI 등)의 특징
順張り 순장 전략
25년 이상 전부터 확립된 개념
→ 파생상품 딜러, 헤지펀드 매니저 등 사이에서 리스크 관리를 위해 지속적으로 활용되고 있는 기법
보통은 '원금보장'이 아님
→ 유동성 리스크 등은 존재
100% 투자보다는 안전함
→ 기본적으로 전체 리스크를 억제하기 위한 기법.
무레버리지의 경우 0~100%까지만 익스포저를 취하기 때문에, 정의상 각 순간마다 전체 투자보다 더 큰 위험은 없다.
장기적(15~20년?)으로는 위험자산과 무위험자산의 포트폴리오를 보유하는 것과 같지만,
단기적(1년 정도?)으로는 하방위험을 효과적으로 제어할 수 있다.

다이내믹 헤지 전략의 기대수익률이란?
다이내믹헤지(DH)가 적용된 주식의 평균 수익률을 다음과 같은 가정 하에 추정
≪전제≫
・ 주식의 기대수익률 = 6%/년
・ 주식의 리스크(표준편차) = 19%/년
・ DH의 Floor 수준=8%/년
・ 정규분포를 가정
・ 몬테카를로 시뮬레이션(10,000회)으로 추정
Simulation 결과
| 주식 100% | DH 부착 주식 100% | 주식 60% + 현금 40% | |
| 평균 수익률 | 6.0% | 3.6% | 3.6% |
| 표준편차 | 19.0% | 13.4% | 11.4% |
| 99% VaR | -38.2% | -8.0% | -22.9% |
- DH부착 주식의 기대수익률은 원 주식의 0.5% 정도에
- DH 편입 주식의 하방위험(VaR) 대폭 축소

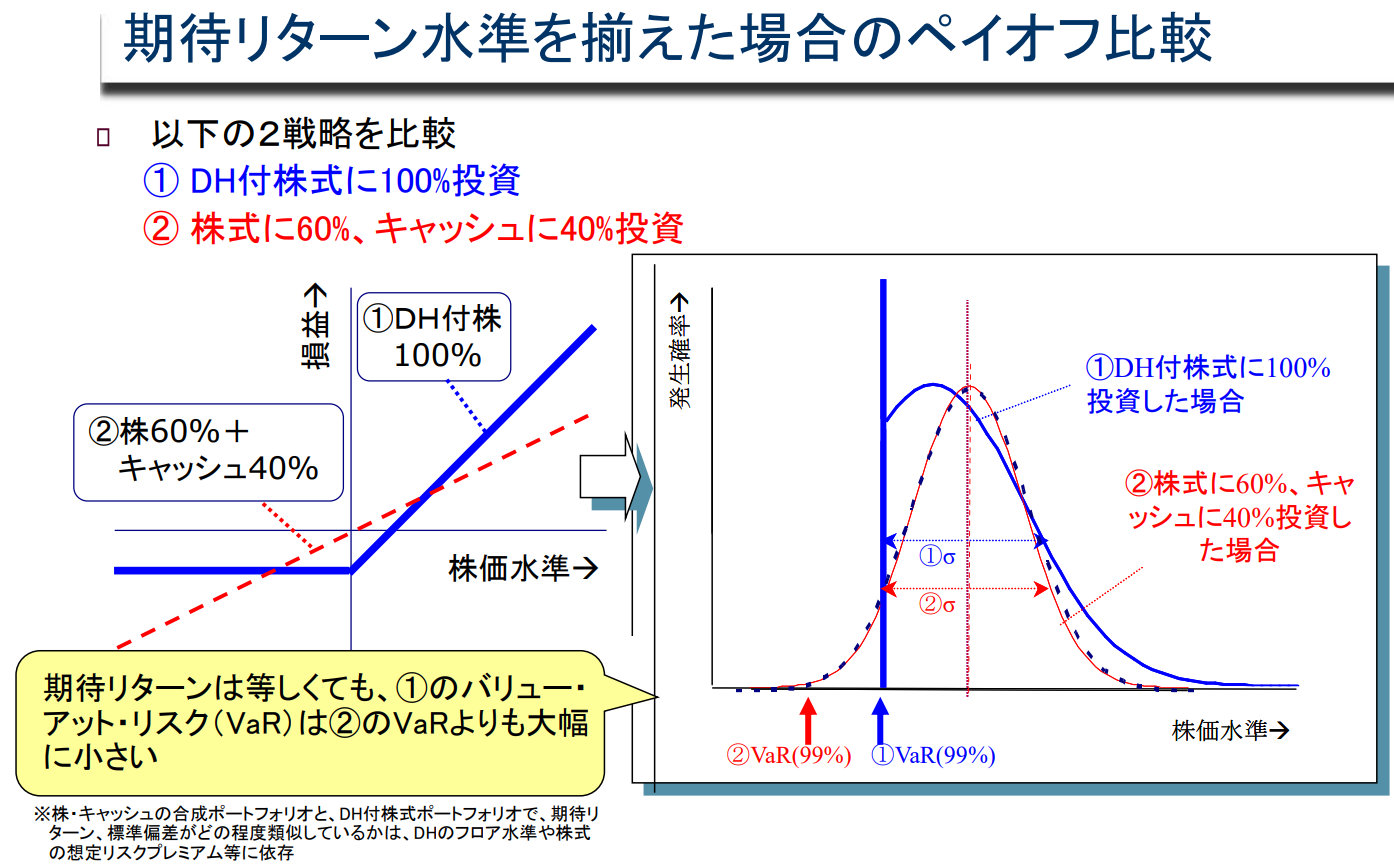
기대수익률 수준별 보상금 비교
다음 두 가지 전략 비교
① DH부 주식에 100% 투자
② 주식에 60%, 현금 40% 투자
기대수익은 같지만, ①의 VaR(Value at Risk)은 ②의 VaR보다 훨씬 작다.
TOPIX 연간 수익률의 특징(1981/4-2011/3)

다이내믹 헤지 도입 효과 예시 (TOPIX, 지난 30년간)
국내 주식에 다이내믹 헤지 전략을 도입한 경우 지난 30년간의 성과 추이는 다음과 같다(시뮬레이션 기준).

MSCI-Kokusai 연간 수익률(엔화 기준)의 특징(1981/4-2011/3)
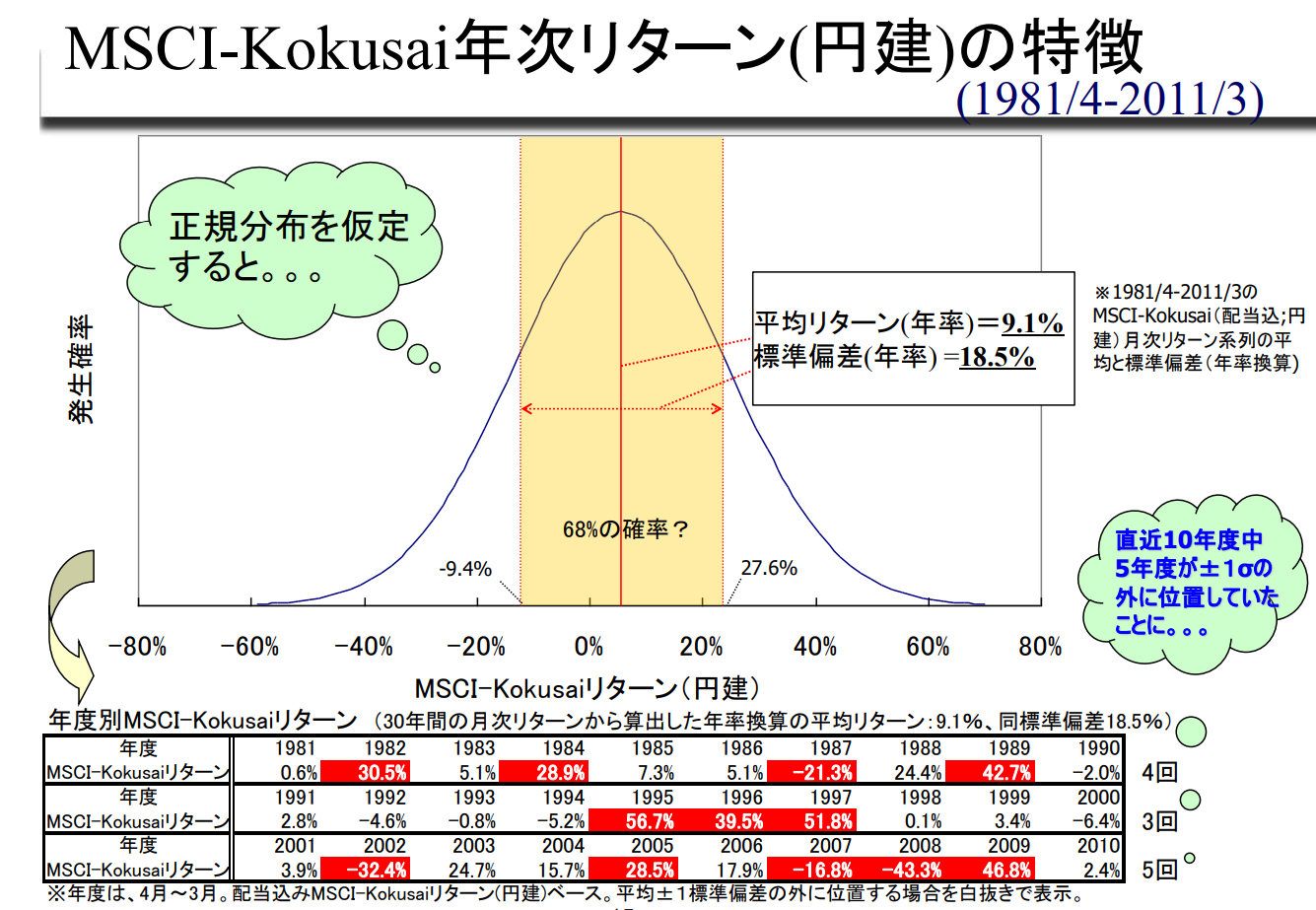
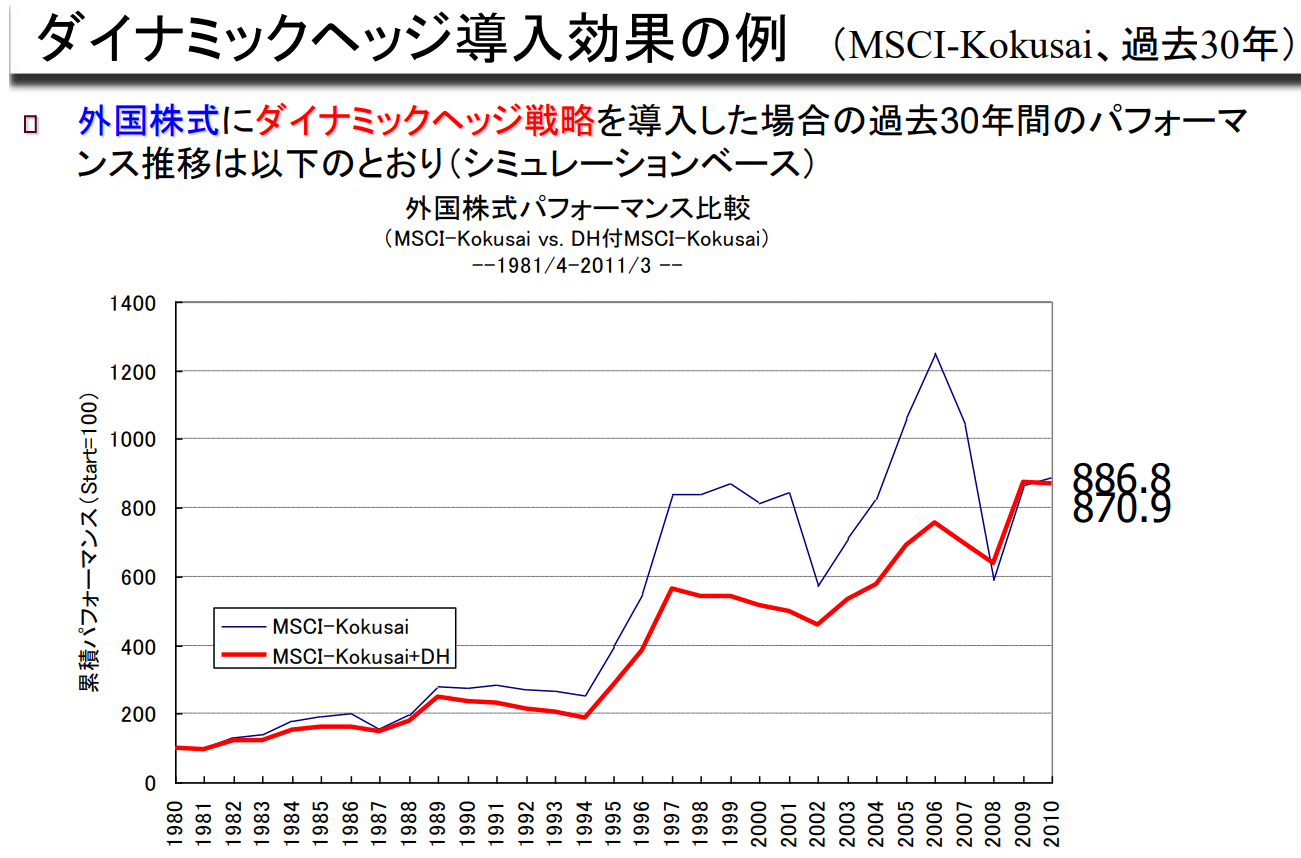
다이내믹 헤지 도입 효과 사례 (MSCI-Kokusai, 지난 30년간)
지난 30년간 해외 주식에 다이내믹 헤지 전략을 도입한 경우의 성과 추이는 다음과 같다(시뮬레이션 기준).
다이내믹 헤지 전략의 유의사항
다이내믹 헷지 전략(순장형)은 유동성 소비형 전략
→ 운용자산이 수 천억 원 정도의 연기금이라면 적용 가능하나, 수 조 원이 넘는 거대 기금은 전면적인 적용은 어려움
→ 유사한 다이내믹 헤지 전략을 채택하는 투자자가 너무 많아질 경우
역발상형 전략(유동성 공급형 전략)에 투자 묘미가 생길 가능성도 있음.
→ 동적 헤지 등 순장형 전략을 채택하는 투자자와 역장형 전략에 충실한 거대 투자자 등이 공존하여
수급 균형이 잡힌 상태에서 시장이 균형을 이루게 될까?

연금기금은 왜 리밸런싱을 하는가?
⇒ 정책적 자산믹스와의 괴리를 제한하기 위해
- 정책적 자산믹스와의 괴리는 기금에 대한 위험으로 인식
~ 시세가 상승할 때 리밸런싱을 주저하고, 이후 시세 반락으로 후회하는 펀드도 있다.
↓
어떤 재균형 구조가 바람직한가?

리밸런싱 방법의 대표적인 예
Calendar Rebalacing
- 월별, 분기별, 반기별 등 정기적인 시간 간격으로 리밸런싱 수행
Range Rebalancing
- 각 자산별 가중치 편차 허용범위(3%, 5%, 10% 등)를 정하고, 다른 자산에서도 허용범위를 초과할 경우 리밸런싱 수행
Active Risk Rebalancing
- 포트폴리오의 정책자산믹스에 대한 액티브 리스크(추적오차)가 일정 범위 이상일 경우 리밸런싱을 수행
현금 흐름 기반 리밸런싱
- 포트폴리오의 현금 유입/유출 범위 내에서만 리밸런싱을 실행합니다.
전술적 리밸런싱
- 박스권에서는 좁은 범위에서, 추세권에서는 넓은 범위에서 리밸런싱 실행 (박스권 및 추세 예측이 필요)

볼록 전략과 오목 전략 비교
수익률의 시계열 상관관계 관점
- 양의 시계열 상관관계(추세)의 경우 볼록 전략(순방향), 음의 시계열 상관관계(박스권)의 경우
오목 전략(역방향)이 유리하다.
위험감수성 관점
- 위험 허용도가 높고, 누적적으로 일정 수준 이상의 수익을 얻을 확률을 높이고 싶다면 오목한 전략이 유리하다.
- 위험 허용도가 높지 않은 경우, 볼록 전략으로 하방위험을 통제하는 것이 효과적 (연기금, 헤지펀드, etc.)
→ 포트폴리오의 위험 수준 자체를 낮추는 것과 대비?

배분 최적화를 위한 노력

전회 복습(제 2, 3회 수업)
전회 복습 (제6회 수업)
배분 최적화를 위한 노력

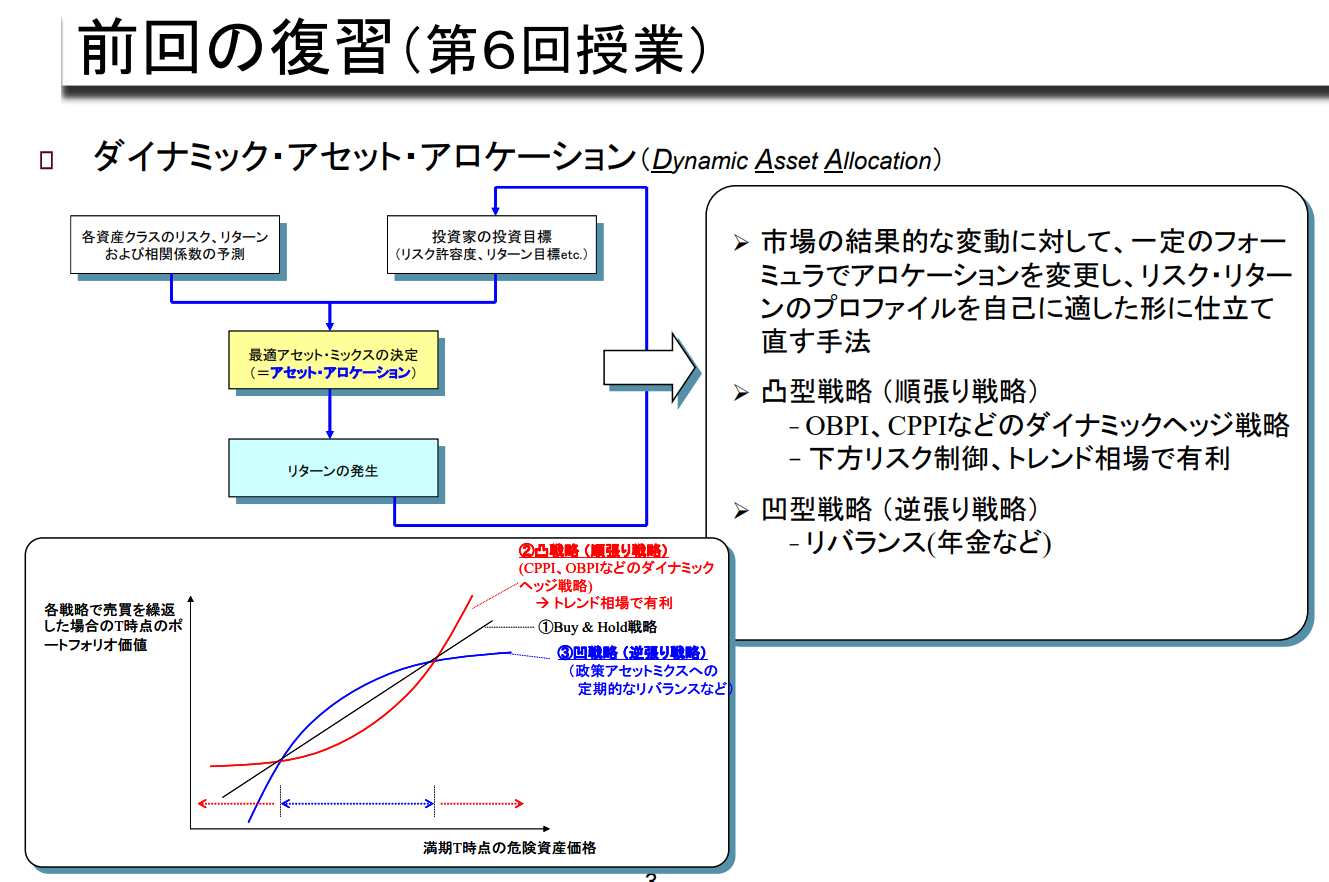
Mean-Variance형 최적화의 특징과 한계는?
Markowitz(1952) 이후 평균=분산형 최적화는 그 유용성-간편성 때문에 이론가-실무자 모두에게 폭넓게 정착
그러나 실무적으로는 다음과 같은 문제점이 지적되고 있다.
- 극단적인 해의 도출이 용이함
- Parameter 추정 오차의 영향력 커 (오차 최대화 문제?)
- 옵션 등 비선형 자산의 정확한 표현 불가
- 절대수익률과 상대수익률 등 여러 관점을 고려하지 못한다.
- 중간중간의 투자행동을 고려하지 못함 (3차원 기간 모델)


최적화를 위한 노력의 예
극단적인 해답이 나오기 쉽다?
→ 가중치 상하한 제약 조건의 활용
→ Black-Litterman형 최적화
파라미터 추정 오차의 영향을 완화하는 방법은?
→ Resampling 방법
수익률 분포의 왜곡, 첨도 등을 고려하려면?
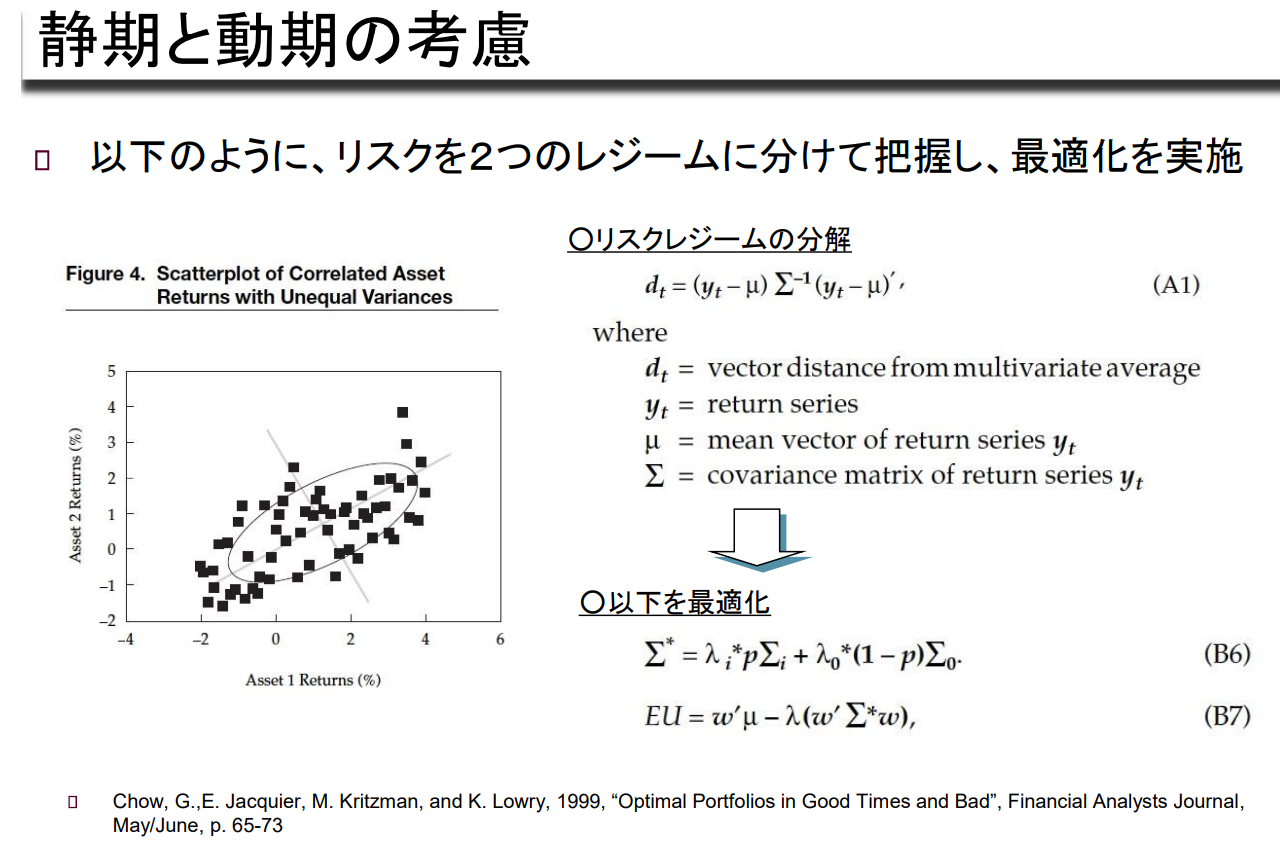
→ M-CVaR 최적화(M-TCE 최적화, M-LPM 최적화), 정기와 동기의 고려
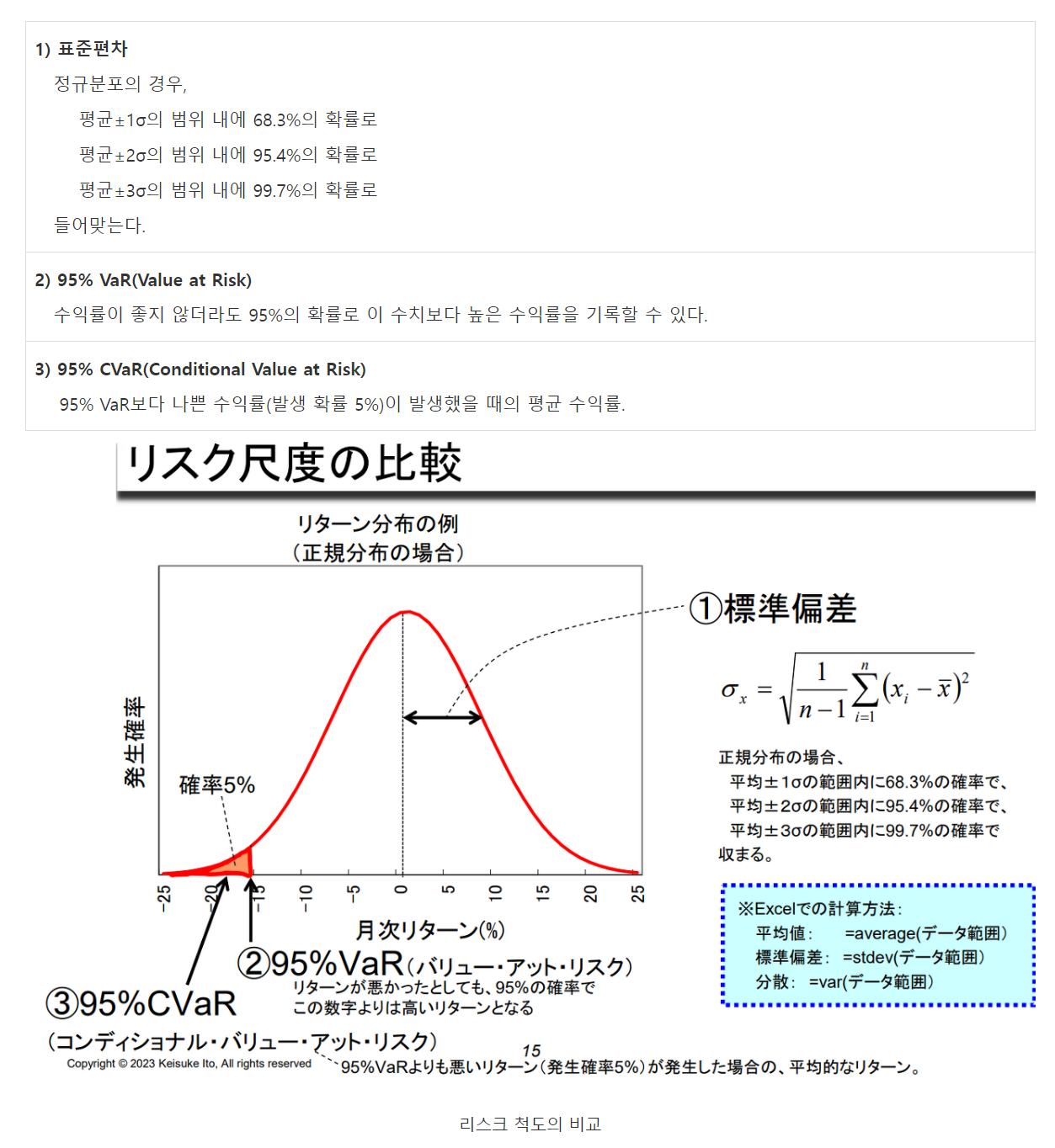
Conditional Value at Risk
중간의 투자 행동까지 고려하려면?
→ 다기간 최적화, SAA

Parameter 추정 오차의 영향에 대한 기존 연구(1)
Michaud[1989], Jorion[1992]
- 파라미터에 추정오차가 있는 경우, 최적화는 오차극대화를 수행한다?
- 평균=분산법에 의한 '최적 포트폴리오'의 근방에는 그것과 통계적으로 동등한* 포트폴리오가 무수히 존재한다.
* 파라미터 추정 오차를 고려하면 '최적 최적가격'이 되어도 이상하지 않을 정도의
최적가격이 존재할 수 있는 포트폴리오를 의미함.
→ 현재의 자산배분비율이 최적의 자산배분비율에서 크게 벗어났다고 판단되는 경우에만
최적의 자산배분비율에 근접하도록 노력하는 등의 운용방식을 고려할 수 있다.

파라미터 추정오차의 영향에 관한 기존 연구(2)
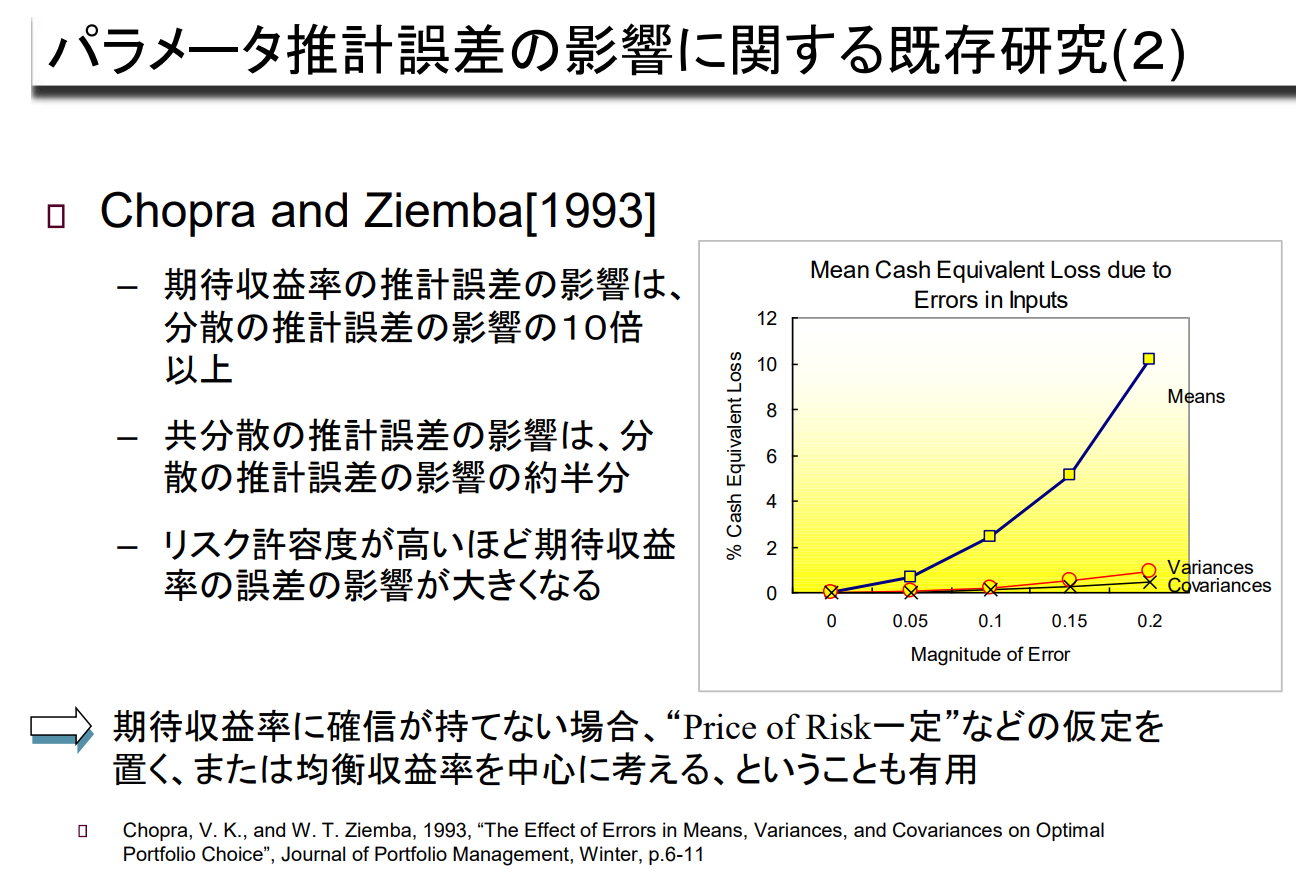
Chopra and Ziemba[1993]
- 기대수익률의 추정오차의 영향은 분산 추정오차의 영향의 약 2배 이상
- 공분산 추정오차의 영향은 분산 추정오차 영향의 약 절반 수준
- 위험 허용도가 높을수록 기대수익률의 오차 영향은 커진다.
→ 기대수익률에 대한 확신이 없는 경우, "Price of Risk 일정"과 같은 가정을 두거나,
균형수익률을 중심으로 생각하는 것도 유용하다.
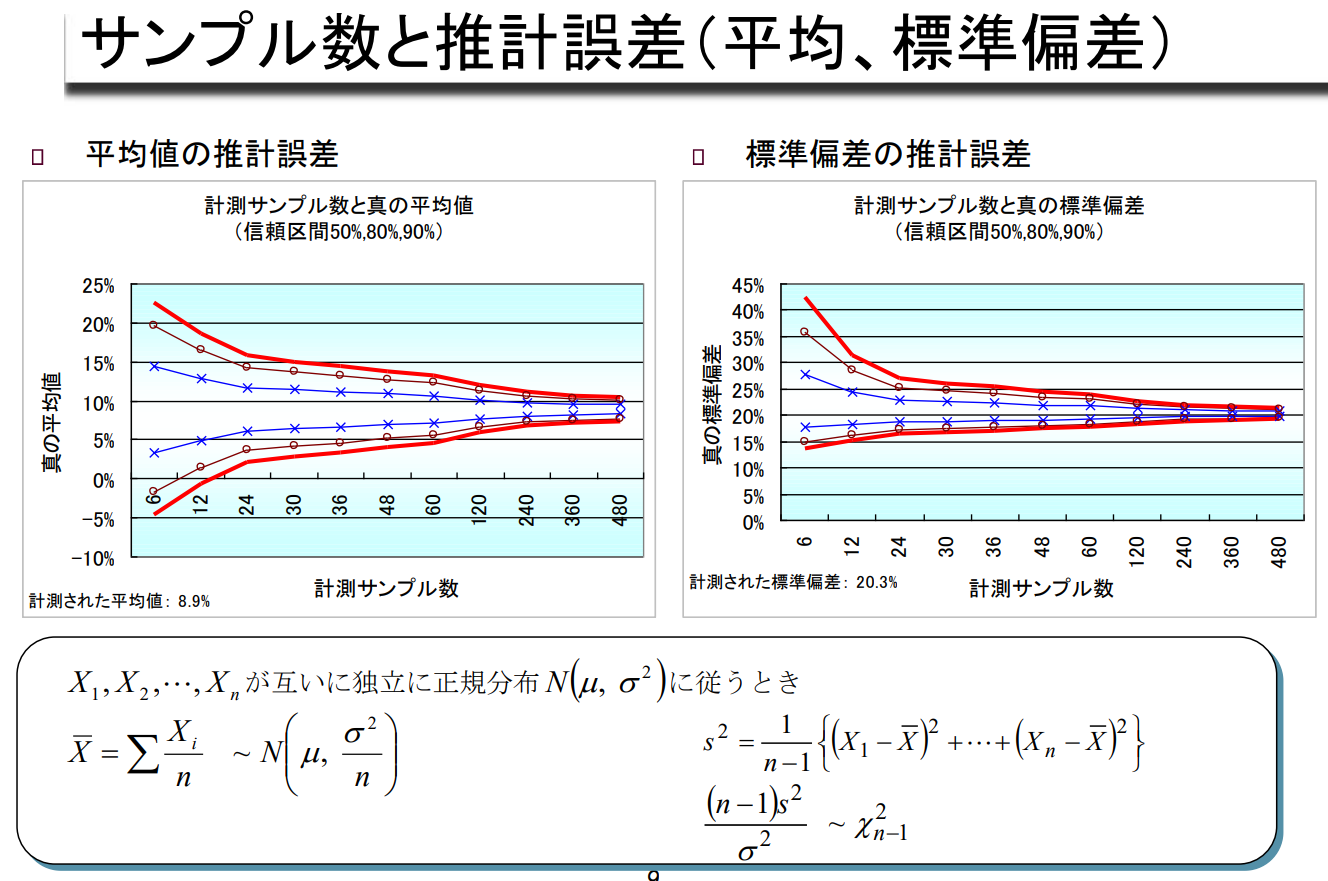
표본 수와 추정 오차(평균, 표준편차)
| 평균값 추정 오차 | 표준편차의 추정오차 |
| 측정 샘플 수와 실제 평균값 (신뢰구간 50%, 80%, 90%) |
측정 샘플 수와 실제 표준편차 (신뢰구간 50%, 80%, 90%) |
N ( μ 6%, σ^2 20%^2 )
↓
25 Samples
X ~ N ( 6% , 20%^2 / 25* ) *20%/5
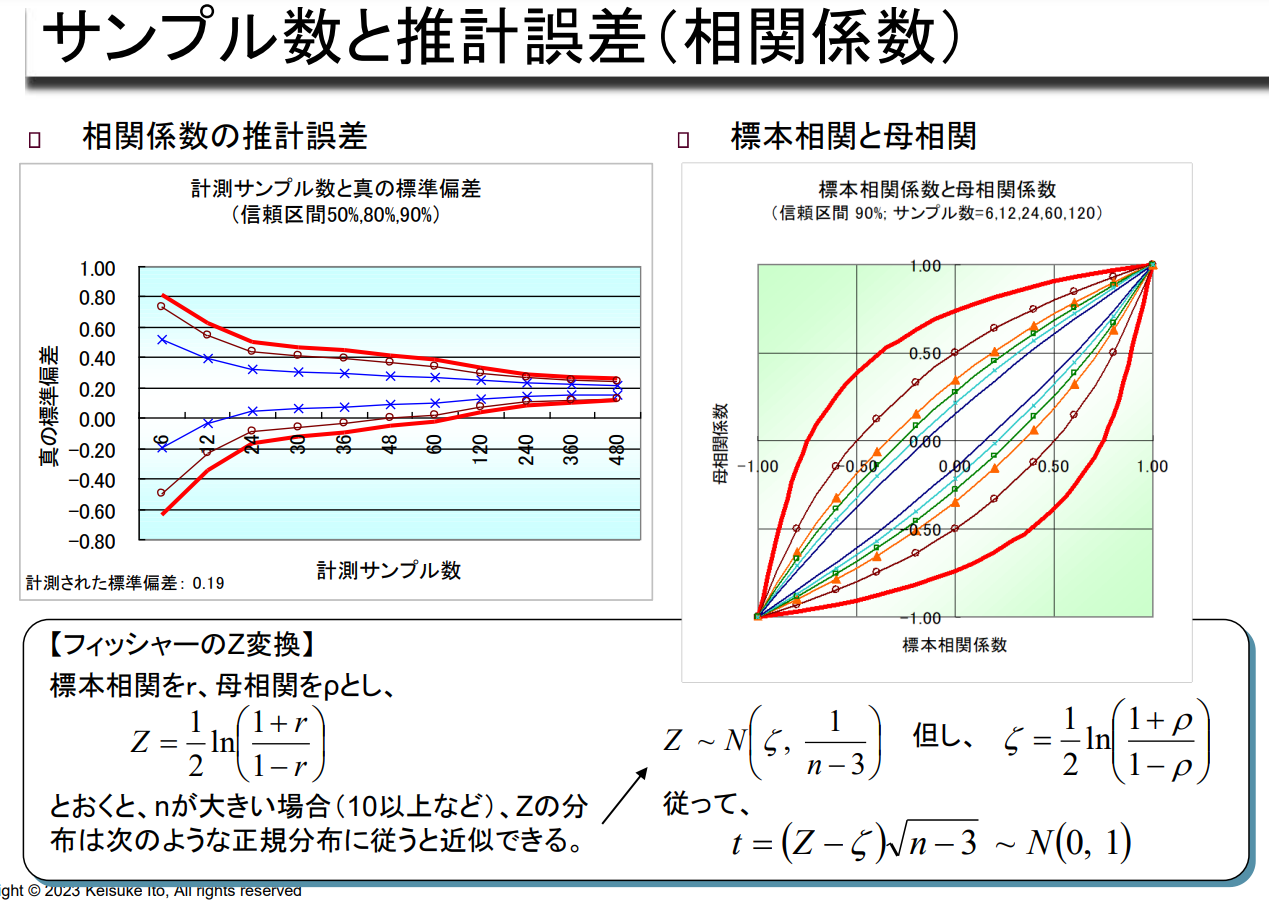
표본 수와 추정 오차(상관 계수)
| 상관 계수 추정 오차 | 표본상관관계와 모상관관계 |
| 측정 샘플 수와 실제 표준편차 (신뢰구간 50%, 80%, 90%) |
표본상관계수와 모상관계수 (신뢰구간 90%; 샘플수=6,12,24,60,120) |
리샘플링 방법이란?
| Step1 | 기대수익률 및 분산공분산 행렬 추정 | ||||
| Step2 |
Step1의 분포에 따른 수익률 샘플을 T개 생성하여 발생시킴. 분포의 표본평균, 표본분산공분산을 측정 |
||||
| Step3 |
Step2의 표본평균-표본분산공분산을 바탕으로 특정 리스크 거부도(또는 목표수익률)의 최적 포트폴리오(또는 프론티어 전체)측정 |
||||
| Step4 |
Step2,3을 수차례 반복한 후, 각 위험거부도(또는 목표수익률)의 최적 포트폴리오 가중치를 평균하고, Step1에서 추정한 기대수익률, 분산공분산 행렬로 평가. |
||||


리샘플링 방법의 효과
확률적으로 동등한 포트폴리오를 평균화하여 극단적인 배분을 피하고 보다 분산된 프런티어를 산출하는 경향이 있습니다.

상관관계 포함 난수 생성 방법

리샘플링 방법에서 "난수"는 무작위로 생성된 숫자를 의미합니다.
이는 통계적 시뮬레이션에서 주로 사용되며, 예측 모델의 불확실성을 반영하는 데 사용됩니다.
여기서 생성된 난수는 특정 확률 분포를 따르도록 설계됩니다.
"상관관계 포함 난수 생성 방법"은 여러 변수의 난수를 생성할 때,
이들 변수 간의 상관관계를 고려하는 방법을 의미합니다.
예를 들어, 투자 포트폴리오의 여러 자산 간의 수익률 상관관계를 고려하여
시뮬레이션을 수행하려는 경우에 사용됩니다.
이를 위한 일반적인 방법 중 하나는 Cholesky 분해를 사용하는 것입니다.
이 방법은 먼저 상관 행렬을 Cholesky 분해하여 하위 삼각행렬을 얻은 다음,
이 하위 삼각행렬과 독립적인 표준 정규 분포 난수를 곱하여 상관관계를 가진 난수를 생성합니다.
이렇게 생성된 난수는 리샘플링 방법에서 사용되어,
투자자가 다양한 시나리오에서 포트폴리오의 성과를 시뮬레이션하고,
이를 바탕으로 최적의 투자 전략을 결정하는 데 도움을 줍니다.
리샘플링 방법에서 "난수"는 무작위로 생성된 숫자를 말합니다.
이 숫자들은 컴퓨터를 사용해 무작위로 생성되며,
이를 통해 우리는 미래의 여러 가능성을 모방할 수 있습니다.
"상관관계 포함 난수 생성 방법"은 두 가지 이상의 것들 사이에 관계가 있다고 알려져 있을 때,
이 관계를 고려하여 난수를 생성하는 방법을 말합니다.
예를 들어, 주식 시장과 부동산 시장은 서로 어느 정도 관련이 있을 수 있습니다.
한 시장에서 무작위 변동이 발생하면 다른 시장에서도 비슷한 변동이 발생할 수 있습니다.
이런 상황을 모방하기 위해, 우리는 두 시장 사이의 관계를 고려하여 난수를 생성합니다.
이렇게 생성된 난수는 리샘플링 방법에 사용됩니다.
리샘플링 방법은 미래의 다양한 시나리오를 시뮬레이션하여,
이를 바탕으로 최적의 투자 전략을 결정하는 방법입니다.
즉, 미래에 어떤 일이 일어날지 모르지만,
우리는 난수를 사용하여 가능한 미래의 시나리오를 '샘플링'하고,
이를 바탕으로 최선의 결정을 내리려고 합니다.

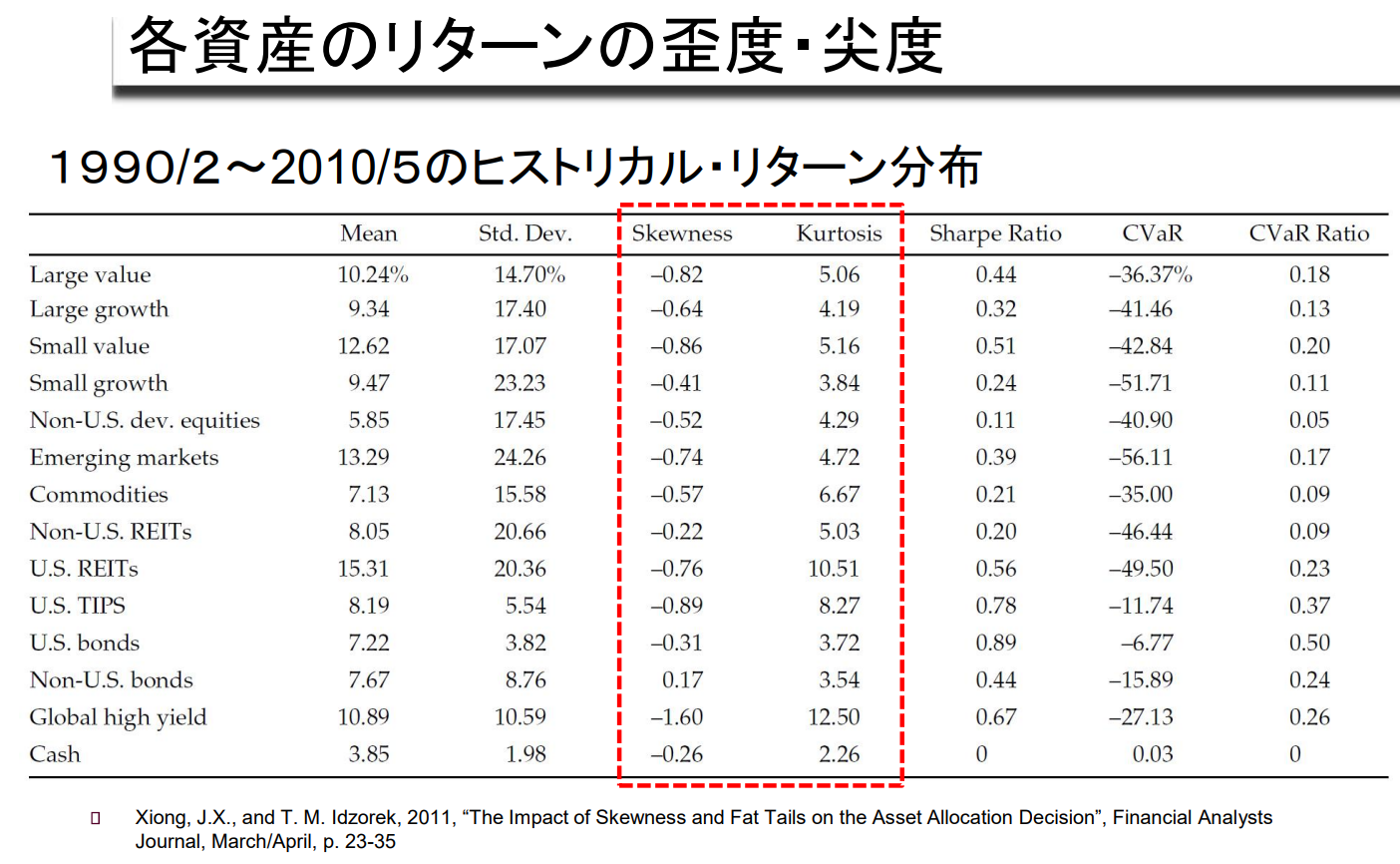
각 자산의 수익률 왜곡도(Skewness) 및 첨예도(Kurtosis)
1990/2~2010/5 Historical Return 분포
**왜곡도 (Skewness)**와 **첨예도 (Kurtosis)**는 통계학에서 확률 분포의 모양을 설명하는
두 가지 중요한 개념입니다.
1. **왜곡도 (Skewness)**:
왜곡도는 확률 분포의 비대칭성을 측정하는 지표입니다.
왜곡도가 0이면 분포는 완벽하게 대칭입니다.
왜곡도가 0보다 크면 분포는 오른쪽으로 치우쳐 있으며 (즉, 분포의 꼬리가 오른쪽에 있음),
왜곡도가 0보다 작으면 분포는 왼쪽으로 치우쳐 있습니다 (즉, 분포의 꼬리가 왼쪽에 있음).
2. **첨예도 (Kurtosis)**:
첨예도는 확률 분포의 꼬리 부분의 두께와 중심 부분의 뾰족함을 측정하는 지표입니다.
첨예도가 0인 정규 분포에 비해
첨예도가 높은 분포는 중심 부분이 더 뾰족하고 꼬리 부분이 더 두꺼운 형태를 가집니다.
이는 극단적인 값 (즉, 아주 크거나 작은 값)이 더 자주 발생함을 의미합니다.
반면, 첨예도가 낮은 분포는 중심 부분이 더 평평하고 꼬리 부분이 더 얇은 형태를 가집니다.
이 두 지표는 주식, 채권, 상품 등 다양한 금융 자산의 수익률 분포를 분석하는 데 사용됩니다.
왜곡도와 첨예도를 이해하는 것은 투자자가 자산의 수익률 분포가
정규 분포를 벗어나는 정도를 파악하는 데 도움이 됩니다.
이는 투자 리스크를 관리하고 최적의 투자 전략을 수립하는 데 중요합니다.
사례 연구
다음 두 가지 패턴의 리스크 억제 방안을 고려해보자.
- 주식을 압축하고 채권을 늘리는 방식으로 리스크 억제
- 포트폴리오의 하방 리스크 관리 차원에서 리스크가 큰 국내 주식 및 해외 주식에 대한 다이내믹 헷지 전략 도입

리스크 억제형 포트폴리오 검토
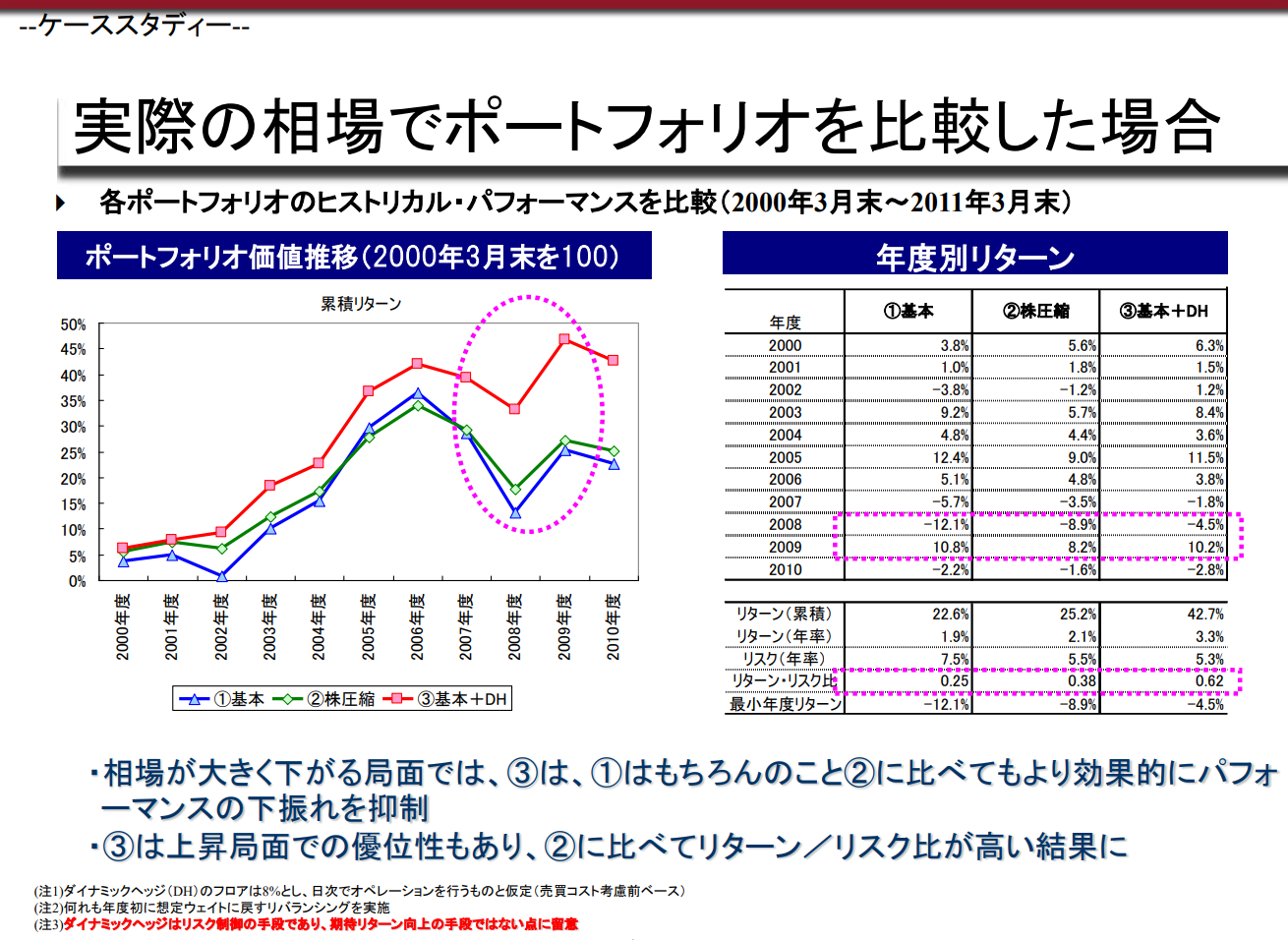
▶ 리스크 억제형 포트폴리오로 다음과 같은 '②주식 압축'과 '③기본+DH' 포트폴리오를 검토
②와 ③은 기대수익률과 표준편차는 비슷하지만,
VaR로 본 하방위험은 ③이 ②보다 크게 낮다(몬테카를로 시뮬레이션 기준).

실제 시세로 포트폴리오를 비교했을 때
정기와 동기의 고려
중간 과제

'WBS - 2023 Fall > 자산배분' 카테고리의 다른 글
| [자산배분 #13-14] (0) | 2023.11.25 |
|---|---|
| (자산배분 #11-12) 대체투자 및 해외 분산투자 | 자산 배분에 대한 성과 평가 (0) | 2023.11.18 |
| (자산배분 #9-10) Strategic Asset Allocation | 개인 투자가의 Asset Allocation | 다기간 Asset Allocation의 실제 (0) | 2023.10.28 |
| (자산배분 #5-6) Tactical Asset Allocation (0) | 2023.10.21 |
| (자산배분 #3-4) 투자방침의 책정 | Policy Asset Allocation (0) | 2023.10.14 |
| (자산배분 #1-2) Asset Allocation의 중요성과 그 Framework (0) | 2023.10.07 |



