와세다 MBA 수업
야간 주 프로그램
기업 재무/거버넌스 연습
No.1
담당 교수: 우치다 교친
E-mail: konari.uchida@waseda.jp

목표
- 재무적 의사결정에 대해 과학적으로 고찰하는 스킬을 습득
- 유명한 이론과 실증 결과의 이해
- 기업 재무/거버넌스의 실증 논문 읽기
- 자신만의 가설 및 연구 디자인을 생각하는 준비

스케줄
| Day 1: 오리엔테이션과 실증 분석의 구성 | 실증 결과의 읽는 방법 |
| Day 2: 실증 분석의 기초: 회귀 분석 | |
| Day 3: 자본 구성에 대한 실증 연구 | 주로 연간 재무 데이터를 사용한 실증 논문을 읽습니다. |
| Day 4: 페이아웃(배당 & 자사주 매입)의 실증 연구 | |
| Day 5: 이사회에 대한 실증 연구 | |
| Day 6: 경영진 보상에 대한 실증 연구 | |
| Day 7: 투자 & 리스트럭처링에 대한 실증 연구 |

| Day 8: 주식 수익률 분석 | 주식 수익률 분석 방법 |
| Day 9: 페이아웃과 주식 수익률 | 기업 이벤트 발표 후의 주식 수익률을 분석한 논문을 읽습니다. |
| Day 10: 주식 발행과 주식 수익률 | |
| Day 11: M&A에 대한 실증 연구 | 연간 데이터와 주식 수익률을 모두 분석한 논문을 읽습니다. |
| Day 12: ESG에 대한 실증 연구 | |
| Day 13: 학생 프레젠테이션 | |
| Day 14: 학생 프레젠테이션 |

실증 논문의 일반적인 구성
- Introduction 소개
- 연구 동기, 간결한 선행 연구 리뷰, 선행 연구의 미비점, 가설, 실증 결과, 기여.
- Literature review and hypotheses 문헌 검토 및 가설 설정 (이론 및 논리)
- Sample selection and data 샘플 선택 및 데이터 (가설을 검증하기 위해 적절한 데이터와 분석 디자인을 선택)
- Empirical results 실증 결과
- 단변량 분석 (오늘)과 회귀 분석 (Day 2)
- Additional analyses/Robustness tests 추가 분석/견고성 검증
- Conclusion 결론

가설을 생각해보기
- X는 Y에 긍정적(또는 부정적)인 영향을 준다
- (예) 기업의 수익성은 배당에 긍정적인 영향을 준다 (기업의 배당은 수익성과 긍정적인 관계에 있다)
연습: 기업 재무/거버넌스와 관련하여 가설을 제시해 주세요.
Y와 X를 무엇으로 할 것인가요?
Y와 X 사이에 긍정적인 관계를 예상하나요, 아니면 부정적인 관계를 예상하나요?

대리 변수(Proxy)를 고려하기
- 대리 변수: X, Y를 나타내는 변수
- 입수 가능한 것
- 데이터의 입수 가능성 때문에, 대리 변수는 반드시 X, Y와 완전히 일치하지 않을 수 있음 (X와 Y는 이론상의 변수)
- 기업 규모와의 상관관계를 약화시키고, 변수의 분포를 정돈하기 위해,
재무제표 데이터를 기업의 규모 변수로 나누어 사용하는 것이 일반적임 - 수익성: ROA (자산 대비 수익률) 또는 ROE (자본 대비 수익률)
- 배당: 배당/자산, 배당/매출, 배당/당기순이익
- 기업 규모의 대리 변수로서, 자산의 자연로그를 사용하는 것이 일반적임
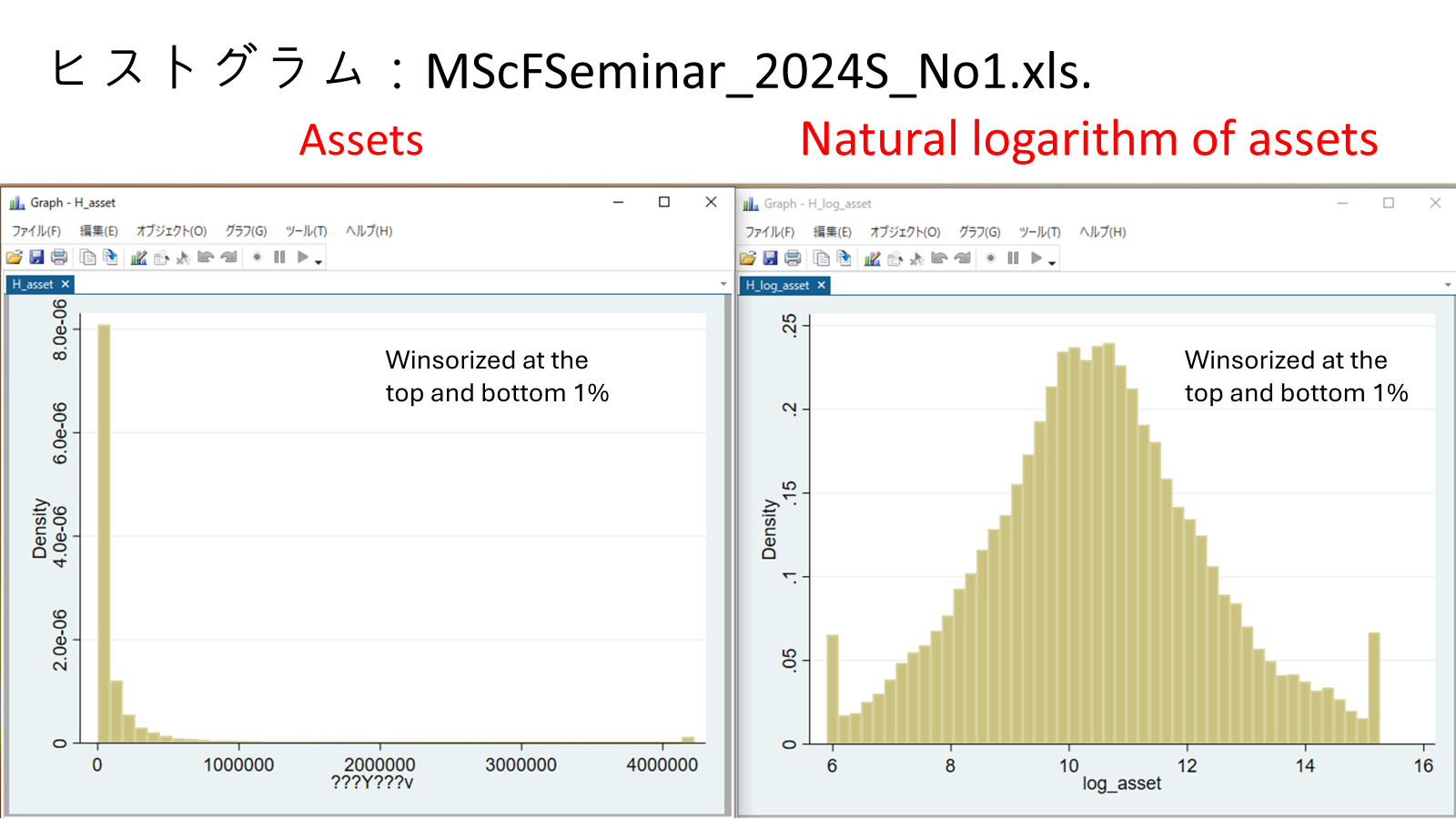
- MScFSeminar_2024S_No1.xls 참조

| 자산 | 자산의 자연로그 |
상위 및 하위 1%에서 윈저화(Winsorized) 처리
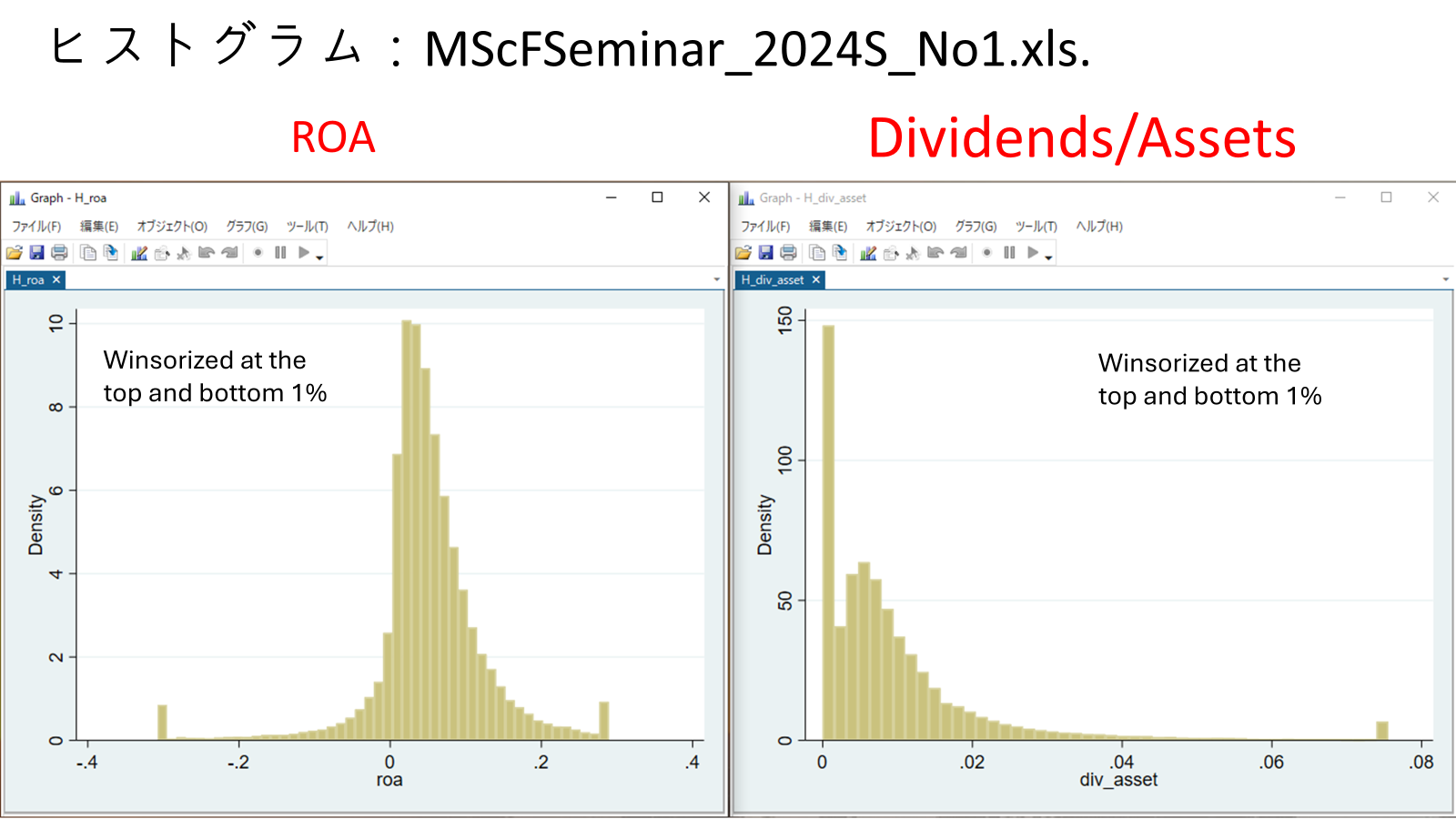
실증 분석
- 가설 검증 방법
- 단변량 분석: X와 Y의 관계만을 주목
- 회귀 분석: 다른 요인들을 통제하면서, X와 Y의 관계를 분석
- 단변량 분석
- 샘플을 X 또는 Y를 기준으로 몇 개의 그룹으로 분할
- 각 그룹의 Y 또는 X의 평균 또는 중앙값을 비교
- 가설이 긍정적인 관계를 예측하고 있다면, X 또는 Y가 높은 그룹은 Y 또는 X의 평균 또는 중앙값이 높아야 함
- 통계적 검정이 필요: 평균의 차이 검정 또는 중앙값의 차이 검정을 실시하여 유의미(Significant)한 차이가 있는지 분석

Dividends/Assets와 ROA의 산포도

평균 차이 검정
- Y를 기준으로 두 그룹을 생성합니다 (H와 L)
- 그룹 H는 그룹 L보다 X의 평균값이 높을 것으로 예상됩니다.
- 기호:
- 그룹 H의 샘플 수: 𝑁_𝐻
- 그룹 L의 샘플 수: 𝑁_𝐿
- 그룹 H에서 X의 샘플 평균: (𝑋_𝐻) ̅
- 그룹 L에서 X의 샘플 평균: (𝑋_𝐿) ̅
- 그룹 H에서 X의 불편 분산: 𝑠_𝐻^2
- 그룹 L에서 X의 불편 분산: 𝑠_𝐿^2

평균 차이의 검정
- 기본적인 생각:
- 두 그룹의 모집단에서 분산이 같다고 가정할 수 있다면, 두 그룹의 모집단 평균이 같을 경우, 다음 값은 자유도 \(𝑁_𝐻+𝑁_𝐿−2\)의 t분포를 따릅니다.
- 간단히 말해서:
- 다음 값의 절대값이 대략 2를 초과한다면, 두 그룹의 평균 사이에 유의미한 차이가 있다고 말할 수 있습니다
(정확한 임계값은 t분포표를 참조).
따라서, 가설을 지지할 수 있습니다.
- 다음 값의 절대값이 대략 2를 초과한다면, 두 그룹의 평균 사이에 유의미한 차이가 있다고 말할 수 있습니다



평균 차이의 검정
- 연습: 다음 정보는 일본 기업의 재무 데이터를 수록한 MScFSeminar_2024S_No1.xls에서 생성된 것입니다. High Dividend, Low Dividend 그룹 간의 ROA 평균 차이에 대한 t값을 계산하고, 배당이 수익성과 긍정적인 관계가 있는지 판단하십시오.

Mean difference test
- Large dividend 그룹은 low dividend 그룹보다 ROA가 유의미하게 높다

평균 차이 검정
- 연습: Andres (2008)는 독일 기업 275개를 사용하여 가족 기업의 성과를 분석하고 있습니다.
다음 슬라이드(Table 3)는 가족 기업과 비가족 기업의 특성을 비교한 것입니다.
결과를 요약하십시오.
- Andres, C. (2008). Large shareholders and firm performance – An empirical examination of founding-family ownership. Journal of Corporate Finance 14, 431-445.


가족 기업과 비가족 기업에 대한 기술적 데이터입니다.
샘플은 1998년 12월 31일 프랑크푸르트 증권 거래소(공식 시장)에 상장된 275개 회사로 구성됩니다.
평균값은 먼저 회사별로 계산된 후 모든 샘플 회사에 대해 평균됩니다.
가족 기업은 창립 가족 구성원이 최소한 25%의 투표권을 보유하거나(적을 경우) 가족 구성원이 경영진 또는 감독 이사회 구성원으로 활동하는 회사로 정의됩니다.
레버리지는 총 부채를 총 자산으로 나눈 값으로 정의됩니다.
수익률 변동성은 이전 60개월 동안의 주가 수익률의 표준편차로 측정됩니다.
별표는 통계적 유의성을 0.01(***), 0.05(**), 0.10(*) 수준에서 나타냅니다.


평균의 검정
- 평균 차이의 검정 외에도, 평균의 검정이 사용됩니다.
- 평균의 검정은 특정한 하나의 그룹의 평균값이 특정한 값과 다른지를 분석하는 데 사용됩니다.
- 기호:
- 샘플 수: 𝑁
- X의 샘플 평균: 𝑋̅
- X의 불편 분산: 𝑠^2
- 기본적인 생각:
- 모집단에서 평균이 μ인 경우, 다음 값이 자유도 𝑁 – 1의 t분포를 따릅니다.

평균의 검정
- 간단히 말해서:
- t값의 절대값이 2보다 크다면, X의 평균값은 μ와 유의미하게 다르다고 할 수 있습니다
(정확한 임계값은 t분포표를 참조하세요).
따라서, 가설을 지지할 수 있습니다.
- t값의 절대값이 2보다 크다면, X의 평균값은 μ와 유의미하게 다르다고 할 수 있습니다
- 연습: 일본 기업의 평균 ROA가 3%보다 높다는 가설을 검증하십시오.

- 일본 기업의 평균 ROA(Return on Assets, 자산수익률)가 3%보다 높다

토론
- 연습: 기업에 요구하는 ROA(Return on Assets, 자산수익률) 수준은 얼마인가요?
그리고 평균적인 일본 기업이 당신의 요구를 충족하는지 검증하세요.

통계적 유의성
- 연습: 귀무 가설이란 무엇인가 설명하십시오.
그리고 "1% 수준에서 유의함", "5% 수준에서 유의함"이라는 표현이 무엇을 의미하는지 설명하십시오.

- 귀무 가설은 검증하고자 하는 가설에 반하는 가설이며, "관계가 없다", "차이가 없다"와 같이 예측합니다.
- "배당은 기업의 수익성과 관련이 있다"는 가설의 귀무 가설은 "배당은 기업의 수익성과 관련이 없다"가 됩니다.
- 분석가가 가지고 있는 데이터는 샘플이라고 불리며, 이는 모집단에서 추출된 것입니다.
분명히 하고자 하는 것은 모집단에 있어서의 관계입니다. - "1%(또는 5%) 수준에서 유의하다"는 말은, 귀무 가설이 옳았더라면, 샘플에서 발생하고 있는 현상이 1%(또는 5%)의 확률로만 발생한다는 것을 의미합니다.
따라서, 귀무 가설이 잘못되었을 가능성이 높다는 것을 의미합니다
(즉, 검증하고자 하는 가설이 옳을 가능성이 높습니다).


통계적 유의성
| 통계적으로 유의하지 않음: 이 샘플 평균은 비교적 높은 확률로 발생합니다. |
통계적으로 유의함: 이 샘플 평균이 발생하는 확률은 매우 낮습니다. |
| 귀무 가설이 옳다면, 샘플 평균은 이 분포에서 발생합니다. | 아마도, 이 샘플 평균은 다른 분포에서 발생했을 것입니다. |


메디안 차이의 검정
- 두 그룹 간에 메디안이 다른지를 검정할 수도 있습니다.
- 자주 사용되는 검정 방법은 Wilcoxon 순위합 검정(Wilcoxon rank sum test)입니다.
- 두 그룹의 관측값을 결합하고, 관심 있는 변수에 대해 순위를 매깁니다.
- 각 그룹별로 순위의 합을 계산합니다.
- 귀무 가설이 옳았다면, 순위 합이 계산된 값보다 크거나(또는 작거나) 될 확률을 계산합니다.
- 확률이 충분히 낮다면, 귀무 가설을 기각할 수 있습니다.
- 메디안이 비슷하다면, 각 그룹의 순위 합은 기대값에 가까워져야 합니다.

메디안 차이의 검정:
- 두 학교의 학생 키 비교
| School1 : 미디안 = 175 | 유의하게 다름? | School2 : 메디언 = 167.5 |
| 전체 랭킹 합계는 ( 1 + 24 ) x 12 = 300 |

Wilcoxon 순위합 검정
- 학교 1의 순위 합계는:
16 + 11.5 + 4 + 9.5 + 19 + 9.5 + 8 + 21 + 6 + 6 + 2.5 + 1 = 114 입니다. - 메디안이 같다면, 순위 합계의 기대값은
1/2 × 12 × ( 12 + 12 + 1 ) = 150 입니다.
- 일반적으로 순위 합계의 기대값은 1/2 × 𝑁1 ( 𝑁1 + 𝑁2 + 1 ) 입니다.
- 다음의 z값은 표준 정규 분포를 따릅니다.
𝑧 = ( 순위 합계 − 순위 합계 기대값 ) / √ ( ( 𝑁1 𝑁2 ( 𝑁1 + 𝑁2 + 1 ) ) / 12 )

Wilcoxon 순위합 검정
- 연습 : 두 학교의 학생들 사이의 신장 메디안이 다른지 검증

- z값의 절대값이 2.078보다 클 확률은 3.77%입니다.
- 메디안의 차이는 5% 수준에서 유의미합니다.
2 x [ 1 - NORM.S.DIST ( 2.078, TRUE ) ]

Wilcoxon 순위합 검정
- 연습: MScFSeminar_2024S_1.xls에서, high div_asset 그룹이 low div_asset 그룹에 비해 ROA의 메디안이 높은지 검증하십시오.

- Z값의 절대값이 89.4799보다 클 확률은 거의 0에 가깝습니다.
- 메디안의 차이는 1% 수준에서 유의미합니다.

메디안 검정
- 메디안 차이의 검정에 더해 메디안 검정도 이용된다.
- 메디안 검정은 어느 한 그룹의 메디안이 특정한 값과 다른지를 검증한다.
- Wilcoxon sign rank test가 주로 사용된다.
- School 1에 대한 메디안 검정:
- School 1의 학생들의 신장 메디안이 170cm를 상회하는지 검증한다.
- 모집단의 메디안이 170cm인 경우(귀무 가설), 12명 중 약 절반은 신장이 170cm를 상회할 것으로 기대할 수 있다.
- 학생들의 신장과 관심 있는 값(170cm)과의 차이(절대값)로 학생들에게 순위를 부여한다.
가장 낮은 값의 학생이 1위가 된다.

메디안의 검정
- 학교 1에 대한 메디안의 검정(계속):
- 귀무 가설이 옳다면, 170cm보다 키가 큰(또는 작은) 학생들의 순위 합의 기대값은
1/2 x 1/2 x 12 x 13 = 39 입니다. - 실제 순위 합계는:
2 + 10 + 3.5 + 3.5 + 6 + 8.5 + 8.5 + 11 + 12 = 65 입니다.
- 귀무 가설이 옳다면, 170cm보다 키가 큰(또는 작은) 학생들의 순위 합의 기대값은
- 다음의 z값은 표준 정규 분포를 따릅니다:
z = [ 순위 합계 - 순위 합계 기대값 ] / [ 𝑁(𝑁+1)(2𝑁+1) / 24 ]

Wilcoxon 부호 순위 검정
- 연습: 학교 1의 학생들의 신장 메디안이 170cm보다 높은지 검증하십시오.

- 절대값이 2.039보다 높아질 확률은 4.14%입니다.
- School1의 키 메디안은 5% 수준에서 유의미하게 170cm보다 높습니다.

수업 운영
- 수업 전:
- 슬라이드를 읽고, Exercises/Questions에 참여하세요.
- Day 3 이후에는 지정된 논문을 미리 읽어두세요.
- 슬라이드 등은 Moodle에서 입수하세요. Moodle에 등록하세요.
- 수업 중:
- 우치다가 설명을 진행하며, 지명된 학생이 Exercises/Questions의 답변을 제시합니다.
- 수업 후:
- 슬라이드를 다시 읽고, Exercises/Questions에 다시 참여하세요.
- 과제가 주어진 경우, 그것에 참여하세요.
- 과제도 Moodle을 사용합니다.

성적 평가
- 과제: 50%
- 수업 내용과 논문 이해를 평가합니다.
- 평소 점수 50%
- 출석
- Exercise/Question에 대한 답변
- 질문 등
- 프레젠테이션

'WBS - 2024 Spring > 기업재무 거버넌스' 카테고리의 다른 글
| (기업재무 #9) 합병 및 인수(M&As)의 기본 | M&A에 관한 실증 논문 (0) | 2024.06.28 |
|---|---|
| (기업재무 #8) 단기 이벤트 스터디 | 장기 주식 수익률 분석 | 단일 요인 모델 | 3요인 모델 | 4요인 모델 (0) | 2024.06.14 |
| (기업재무 #7) 투자와 현금흐름 | 제약기업의 투자에 관한 실증 논문 (0) | 2024.06.06 |
| (기업재무 #6) 에이전시 이론과 경영자 보상 | 경영자 보상에 관한 실증 논문 (0) | 2024.05.31 |
| (기업재무 #5) 이사회에 관한 전통적인 견해 | 이사회에 관한 실증 논문 (0) | 2024.05.24 |
| (기업재무 #4) 배당의 대리인 이론 | 배당에 관한 실증 연구 논문 읽기 (0) | 2024.05.14 |
| (기업재무 #3) 자본 구성의 트레이드오프 이론 | 자본 구성 선택에 대한 실증 연구 (0) | 2024.04.25 |
| (기업재무 #2) 실증 분석의 기초: 회귀 분석 (0) | 2024.04.18 |



