Finance에 있어서 [Risk]의 개념, 그리고 Risk의 정량화 방법을 설명하여,
Portfolio에 개별 주식의 Risk와 Return의 관계를 고찰한다.
그리고, Portfolio 이론, CAPM(자본자산평가Model)에 대해 설명한다.
마지막으로, 주가에는, 현재 입수 가능한 모든 정보가 완전히 반영되어있다고 하는
효율적 시장 가설에 대해 설명한다.
2.1 Risk란
Risk가 없는 기업은 존재하지 않는다!
[위기]
Risk란 위험(Danger)와 기회(Opportunity)의 양방을 포함한다.
급격하게 주가가 내려가더라도 [Risk가 높다] 라고 말하지 않는다!
주식투자의 Risk가 높은 것은, 급격한 가격 변동을 예측할 수 없기 때문이다.
Finance의 세계에서는, Risk란, 예측할 수 없는 [불확실성]을 말한다.
Return의 불규칙함이 Risk의 대소를 나타낸다.

Image로 Risk를 잡는다
1,774일 중 일차 Return이 0%~5%인 것은 몇일인지를 보는 방법이다.

올라온 부분의 폭이 좁으면 Risk는 작고,
역으로 폭이 넓으면 Risk는 크다고 한다.

2.2 평균과 표준편차
통계의 제1관문은 의외로 간단
Risk란 장래의 불확실성이다 라고 정의된다.
불규칙함의 크기를 나타내는 것이, 표준편차(Standard Deviation) 등의 통계량이다.
먼저 처음에, 표준편차와 분산(Variance)라고 하는 두 가지 개념이 있다.
통계학에서는 [표준편차는 분산의 평방근이다] 라고 배운다.
그리고 분산은, [Data의 평균치와 각각의 Data의 차를 2승한 것의 합계를 Data로 나누어 구한다] 라고 한다.
Data가 3개 있을 경우, 분산은 다음의 식으로 정의된다.
분산 = {(X1 - X)^2 + (X2 - X)^2 + (X3 - X)^2} / 3
단, X는 3개의 Data의 평균을 나타낸다.

표준편차의 정체란
실무 상에서는, 분산의 단위를 Return의 단위로 동일한 %로 한다.
그러기 위해서는, 분산의 평방근(Root)를 계산하여, 불규칙성의 지표로 하는 것이 일반적이다.
이것을 표준편차라고 한다.
실무 상에서는 대부분의 경우, Volatility 는 이 표준편차를 가리킨다.
표준편차란 Return의 불규칙함을 나타내는 지표다.
따라서, 이 표준편차가 크면 클수록, 그 주식의 Risk는 높다 라고 할 수 있다.
Return의 확률분포

이 분포를 정규분포(Normal Distribution)이라고 하며,
Finance 및 경제의 응용으로 가장 잘 사용되는 확률분포다.
정규분포의 특징은, 평균과 표준편차의 2가지 Parameter가 결정되면 완전히 특정할 수 있는 점이다.
따라서, 종종 정규분포는, 평균 μ, 분산 σ^2의 경우, N(μ, σ^2)로 표시된다. (μ : 뮤, σ : 시그마)
정규분포의 성질
- 정규분포는, 평균 μ을 중심으로 좌우 대칭이 된다.
- 정규분포는, 평균 μ의 위치에서 가장 높아지며, 중심에서 멀어질수록 끝없이 아래의 선에 가까워진다.
- 정규분포의 Curve의 아래 면적은 형태와 상관없이, 어느것도 1이 되며,
분포의 Curve의 아래 면적은 확률을 나타낸다.
- 평균에서 좌우로 표준편차 1개분의 구분,
즉, [평균치±표준편차(σ)x1]의 구간에 데이터가 들어갈 확률은 68.27%이다.
- 평균에서 좌우로 표준편차 2개분의 구분,
즉, [평균치±표준편차(σ)x2]의 구간에 데이터가 들어갈 확률은 95.45%이다.
- 평균에서 좌우로 표준편차 3개분의 구분,
즉, [평균치±표준편차(σ)x3]의 구간에 데이터가 들어갈 확률은 99.73%이다.
평균 70점, 표준편차 8점의 테스트는 70±8점, 즉 62점과 78점의 사이의 학생이 대략 68%가 들어가있다고 알 수 있다.
편차치는 테스트의 점수가 정규분포가 된다고 가정하고,
그 분포가 평균 50점, 표준편차 10이 되도록 득점을 변환한 것이다.
편차치 = ( 원래 득점 - 평균점 ) / 표준편차 x 10 + 50
[평균치±표준편차x1]의 구간, 즉 편차치가 40~60의 수험자는 전체의 약 68%를 점하는 것이 된다.
또한, [평균치±표준편차x2]의 구간, 즉 편차치가 30~70인 수험생은 전체의 약 95%를 점한다.
귀금속의 가격의 Volatility는?
과거 1년간의 평균가격이 780달러, 표준편차가 50달러라고 해본다.
즉, 과거 1년간의 가격의 분포가 정규분포를 따른다고 하면, 가격은 730~830(780±50)달러에 있을 확률은 약 68%이다.
여기서 변동계수(CV : Coefficient of Variation)에 대해 설명한다.
변동계수는,
표준편차 σ 를 평균 μ 으로 나눈 수치로, 상대적인 불규칙 정도를 나타내는 지표 중 하나다.
변동계수 CV = 표준편차 σ / 평균 μ
따라서, 변동계수를 사용하는 것으로 단위가 다른 2개의 통계 Data의 불규칙 정도를 비교하는 것이 가능하다.

2.4 Portfolio에 의한 분산투자 - Return과 분산을 구하는 방법
시장 Risk와 개별 Risk
투자를 분산화하는 것에 의해, Risk를 감소하는 것이 가능하다.
투자가가, Portfolio에 포함하는 종목의 수를 늘려가면, 그것에 따라 Portfolio의 Risk는 감소하게 된다.
그러나, 주식이 일정 수를 초과하면 Risk는 감소하지 않게 된다.
이것은 주식의 Risk 중, 시장 Risk 라고 불리는 것은, 분산화에 의해서도 제외하지 못하기 때문이다.
실은, 주식의 Risk는, 시장 Risk(Market Risk)와 개별 Risk(Unique Risk)의 합계이다.
주식의 Risk
주식의 Risk(Total Risk) = 시장 Risk(Market Risk) + 개별 Risk(Unique Risk)

충분히 분산화된 Portfolio의 Risk는, 그 Portfolio가 포함하는 주식의 시장 Risk에 의해 결정된다.
시장 Risk와 B(Beta)
이처럼, 충분히 분산화한 Portfolio는 시장 Risk만이 문제가 된다.
또한, 투자가가 주목하고 있는 것은, 이 분산화되지 않는 Risk인 시장 Risk이다.
개별 주식의 시장 Risk는, 시장 Portfolio에 대한 감응도를 나타내는 B(Beta)로 측정할 수 있다.

B(Beta)의 정의
B = Cov ( r(i), r(m) ) / Var ( r(m) )
B = { σ(i) / σ(m) } x p(im)
B = ( 주식i의 표준편차 x 주식i와 시장 Portfolio의 상관계수 ) / 시장 Portfolio의 표준편차
r(i) : 주식i의 Return, r(m) : 시장 Portfolio의 Return, p(im) : 주식i와 시장 Portfolio의 상관계수,
σ(i) : r(i)의 표준편차, σ(m) : r(m)의 표준편차

B는 시장 Portfolio에 대한 감응도다.
상관계수란, 주식i와 시장 Portfolio가 어느정도 연동해서 움직이는지의 지표다.
상관계수 +1이 완전상관이다.
예를들어, 상관계수가 0.8의 경우는 0.2의 부분은
시장 Portfolio의 움직인과 관계가 없는 개별 Risk에 해당하는 부분이다.
개별 Risk가 커지면 커질수록, 상관계수는 저하한다.
그 결과, B가 저하하는 것이 된다.
투자가가 1개의 주식에 투자하는 경우, 그 주식의 Total Risk(개별 Risk + 시장 Risk),
즉 표준편차의 크기에 따라서, 높은 수익률을 요구할 것이다.
그러나, 투자가가 Portfolio에 투자하는 경우, 개별 주식의 Total Risk(표준편차)가 아니라,
분산투자에 의해 제거할 수 없는 시장 Risk의 크기가 중요해진다.
B의 계산식의 분자에서, 주식i의 표준편차에 [주식i와 시장 Portfolio의 상관계수]를 곱하는 것은,
주식i의 Total Risk(표준편차)로부터 시장전체에 연동되는 부분(시장Risk)만을 발라내는 것이라고 할 수 있다.
이것은, Total Risk가 같은 주식이라 하더라도 시장 Portfolio와의 상관관계에 차이가 있는 경우,
투자가의 요구하는 수익률은 다르다는 것을 의미한다.

이 직선의 기울기의 1.3116은 TOPIX의 Return이 1% 증가하면,
MUFG의 월차 Return이 1.3116% 증가한다는 것을 나타낸다.
실은, 이 때의 직선의 기울기 1.3116을 B라고 한다.
기울기가 1보다 크다는 것은, MUFG의 주식이 TOPIX에 대해 감응도가 높다고 하는 것을 나타낸다.
즉, B(Beta)란, TOPIX(시장 Portfolio)의 Return이 1% 변화할 때, 그 주식의 Return이 몇 % 변화하는가라는,
TOPIX의 수치 변동에 대한 감응도를 나타내고 있다.
B(Beta)의 수치 특징
TOPIX와 완전히 동일한 수치 변동을 하는 주식의 B는 1로 한다.
예) TOPIX의 가치 움직임이 ±10%의 경우
주식A는 ±20% 가치 변동함 → B = 2
주식B는 ±5% 가치 변동함 → B = 0.5
B는 분산화에 의해 제외할 수 없는 시장 Risk를 측정하는 지표다.
증권시장선의 진실
- 투자가는 Risk에 부합한 Return을 요구한다.
Finance의 세계에서는, 투자가는 Risk 회피적(Risk Averse)이다 라는 것이 전제로 되어있다
요구(기대)수익률 = Risk Free Rate + Risk Premium
예를 들어, Risk Free Rate인 국채의 이자가 1%고, 주식투자의 요구수익률이 6%라고 한다.
[국채에 투자하면, 1%의 Return이 있으니, Risk인 주식투자라면, 최저 6% 정도의 Return이 필요하다] 라는 것이다.
이 때, 요구수익률과 Risk Free Rate의 차이인 5%를 [Risk을 취하는 것에 대한 보상]이라는 의미로,
Risk Premium이라고 한다.
- B와 Risk Premium의 관계
국채는, Risk Free 자산으로, B는 Zero가 된다.
이 때의 Risk Premium도 또한, Zero가 된다.
국채 투자에 [Risk를 취하는 것에 대한 보상] 등이 있을리 없다.
B가 Zero일 경우는, Risk Premium도 Zero다.
시장 Portfolio는 평균적인 시장 Risk를 보유하고 있어서, B는 1이라고 한다.
시장 Portfolio의 기대수익률을 E ( r(m) ), Risk Free Rate를 r(f)라고 하면,
이 때의 Risk Premium은 E ( r(m) ) - r(f) 이 된다.
이 시장 Portfolio의 기대수익률과 Risk Free Rate의 차이를 Market Risk Premium이라고 한다.
따라서, B가 1일 때는, Risk Premium은 E ( r(m) ) - r(f) 라는 것을 알 수 있다.
그렇다면, B가 0이나 1 이외의 수치를 취할 때의 Risk Premium은 어떨까.
이 답에 대답해줄 수 있는 것이 자본자산평가모델 (CAPM : Capital Asset Pricing Model)이다.
CAPM은 Finance 이론에서 가장 중요한 개념 중 하나로,
이 모델의 발견자인 윌리엄 샤프는, 1990년에 노벨 경제학상을 수상했다.
CAPM에 의하면, 모든 자산의 Risk Premium은, 그 자산의 B에 비례한다.
이것이 의미하는 것은, B가 2배, 즉 Risk가 2배가 되면, Risk Premium도 2배가 된다는 것이다.
자산i의 B를 B(i)라고 하면, 자산i의 기대 Risk Premium E ( r(m) ) - r(f) 은,
E ( r(i) ) - r(f) = B(i) x E ( r(m) ) - r(f)
로 나타낸다.
여기서 E ( r(i) )는 자산i에 기대되는 수익률을 나타낸다.
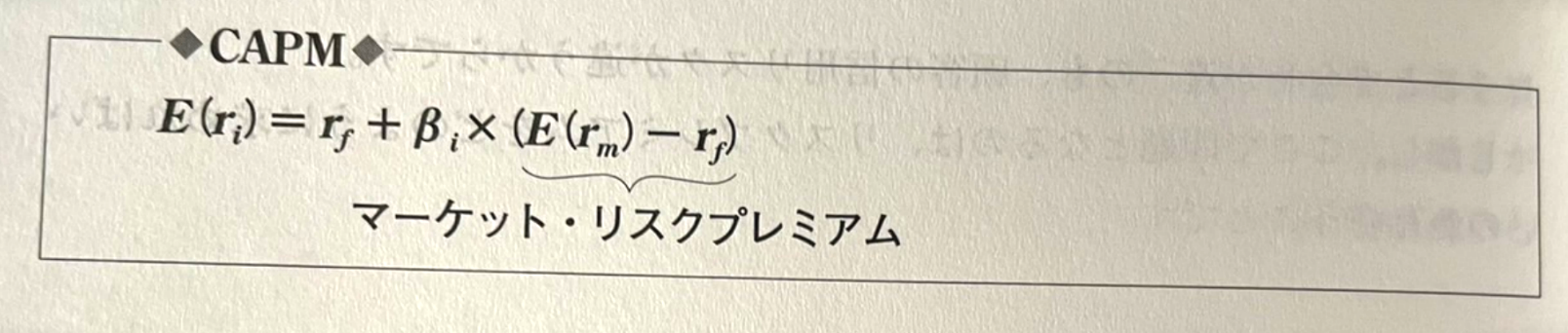
예를 들어, 국채의 이자가 1%, 시장 Portfolio의 기대수익률이 5%일 경우,
B가 1.5의 주식i의 기대수익률 E ( r(i) )는 어떻게 될 것인가.
E ( r(i) ) = r(f) + B(i) x E ( r(m) ) - r(f) = 1% + 1.5 x ( 5% - 1% ) = 7%
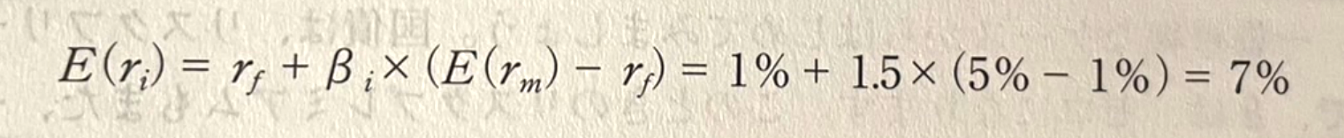
이러한 1차식으로 표시된 직선을, 증권시장선 (SML : Security Market Line)이라고 한다.
증권시장선에서, 모든 자산의 Risk와 Return의 관계를 나타내는 것이 가능하다.

자본시장선(CML)이 Risk를 Total Risk의 척도인 표준편차로 측정하는 것에 대해,
이 SML은 Risk를 시장Risk의 척도인 B로 측정하고 있다.
CML이 그리고 있는 것은, Risk 자산인 시장 Portfolio와 Risk Free 자산을 조합하면서
가능한한 모든 투자가에게 공유되는 효율적 Portfolio인 것에 비해,
SML은 모든 개별주식이나 채권, Portfolio 등의 기대수익률과 B의 관계를 나타내고 있다.
다시 말해, CAPM은 모든 주식 및 Portfolio은, SML의 위에 있다 라고 말할 수 있다.
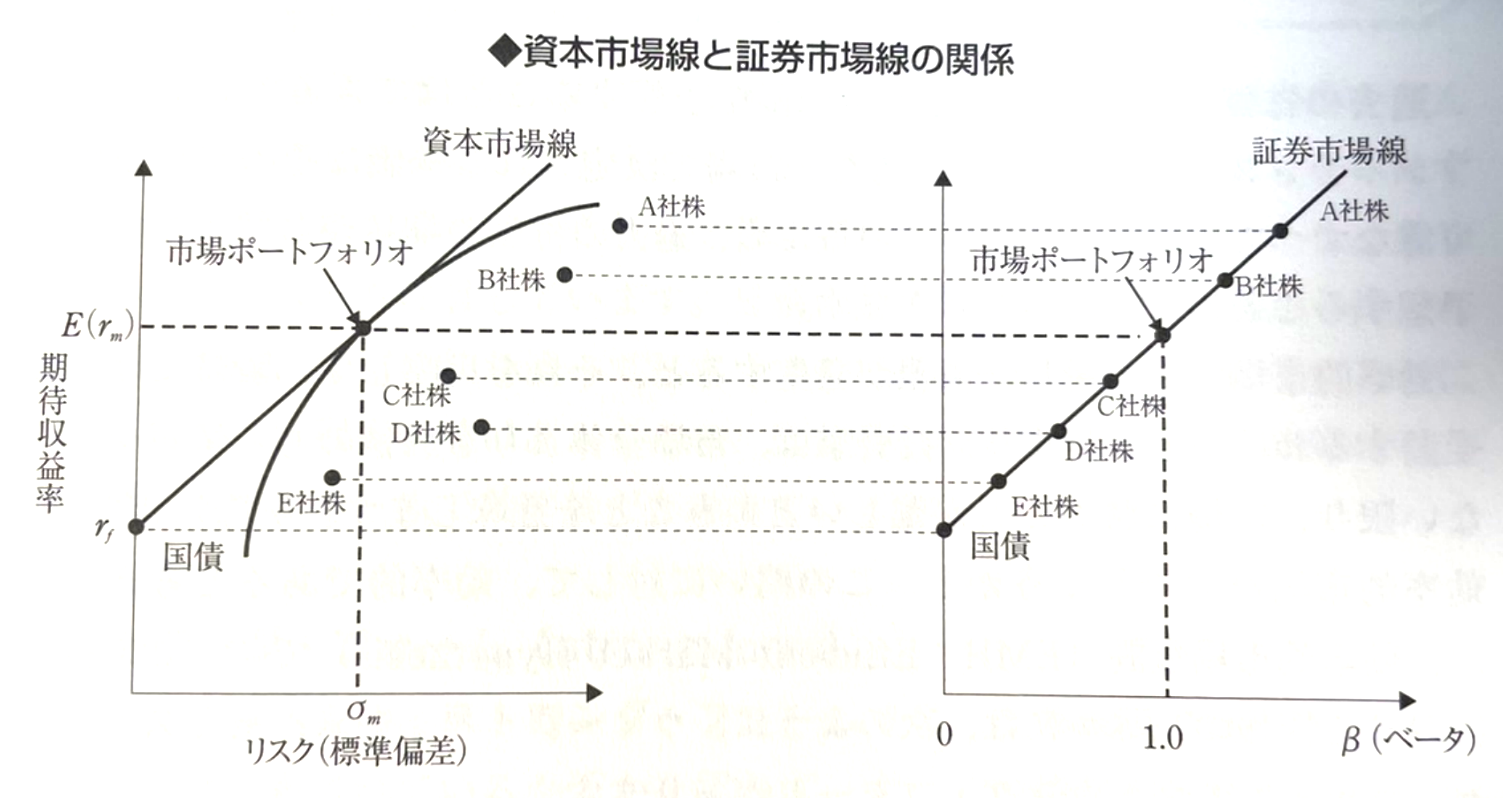
물론 모든 증권이 항상 SML 위에 있다고 할 수 없다.
증권에 따라서는, 낮거나 높은채로 방치되는 것도 있다.
그러나, CAPM의 세계에서는 이런 방치된 증권도, 언젠가는 SML 상에 배치된다고 생각하는 것이다.
제2장 정리
- Risk란 [상정된 결과]의 불규칙이며, 예상하는 것이 불가능한 [불확실성]이라고 할 수 있다.
- 주식의 Risk는 기대수익률(Return)의 표준편차로 측정할 수 있다.
- 공분산은 2변수의 상관관계의 방향성을 나타내는 지표로, 상관계수는 상관관계의 강도를 나타내는 지표다.
- Portfolio의 기대수익률(Return)은, Portfolio에 포함된 주식의 기대수익률의 가중평균이다.
또한, Portfolio의 Risk(분산)은, 주식간의 공분산(상관관계의 방향성)에 따라, 분산효과의 크기가 결정된다.
- 효율적 Frontier는 같은 Risk(표준편차)이면, 기대수익률이 최대인 것,
나아가 같은 기대수익률이면, Risk(표준편차)가 최소인 투자기회의 집합이다.
- 상관계수와 Portfolio의 Risk 분산효과의 관계는, 상관계수가 +1의 경우, Risk 분산효과는 없다.
한편, 상관계수가 -1의 경우는, 2개의 주가가 완전히 반대의 움직임을 하기에,
2개의 주식의 조합 비율에 의해서, Risk Free(표준편차 Zero)로 하는 것이 가능하다.
- 모든 투자가의 최적 Portfolio는, 국채와 시장 Portfolio를 조합한 Portfolio가 된다.
시장 Portfolio는 시장에 있는 모든 주식과 증권을 일정 비율로 보유하는 Portfolio이다.
- 주식의 Risk는, 분산 불가능한 시장 Risk와 분산 가능한 개별 Risk의 합계이다.
충분히 분산화된 Portfolio의 Risk는, 그 Portfolio에 포함되는 주식의 시장 Risk에 의해서 정해진다.
- 주식의 시장 Risk는 그 주식의 B(Beta)에 의해서 측정할 수 있다.
- CAPM에 따르면, 모든 주식의 Risk Premium은, 다음 식으로 나타낼 수 있다.
주식의 Risk Premium = B x Market Risk Premium
(Finance) 도구로서의 파이낸스 | 제3장 기업가치평가
Corporate Finance에서, 가장 중요한 개념인 자본 Cost의 고찰과 그 계산방법에 대해서 설명합니다. 또한, 투자가(주주와 채권자)에 귀속하는 Free Cash Flow의 개념을 설명하여, 기업가치평가산정의 Skill
fastcho.tistory.com
'WBS - 2023 Spring > Finance' 카테고리의 다른 글
| (Finance) 네이피어의 수 (0) | 2023.05.24 |
|---|---|
| (Finance) 도구로서의 파이낸스 제6장 Derivatives의 이론과 실전적 지식 (0) | 2023.05.23 |
| (Finance #9-10) (0) | 2023.05.23 |
| (Finance) 도구로서의 파이낸스 | 제4장 기업의 최적자본구성과 배당·자사주 구입 (0) | 2023.05.16 |
| (Finance #7-8) 가준평균자본 Cost (WACC) 와 정리 (0) | 2023.05.08 |
| (Finance) 도구로서의 파이낸스 | 제3장 기업가치평가 (0) | 2023.05.02 |
| (Finance #5-6) Free Cash Flow와 주식(기업가치)의 평가 (0) | 2023.05.01 |
| (Finance) 도구로서의 파이낸스 | 제5장 자본시장에 관련한 이론 (0) | 2023.04.25 |



