사업자금을 조달하는 방법은, 은행에서의 차입 등의 간접금융과,
주식 및 사채의 발행 등의 직접금융의 2개로 나누어지는 것은 이미 설명했다.
이 장에서는 기업의 자금조달 수단인 채권과 주식발행의 구조와,
그 가치의 평가방법에 대해서 설명한다.
그리고 채권의 RISK로서, 신용RISK와 가격변동RISK에 대해 설명한다.
5.1 채권이란
채권이란
발행 시 정해진 조건에 따라서, 정기적으로 일정의 이자를 지급하고,
소정의 만기일에 액면금액을 상환하는 것을 발행체가 약속하고 있는 증권
발행체가 도산하지 않는 한, 만기일까지의 Cash Flow가 확정되어 있는 것으로부터
확정이자부증권(Fixed Income Securities)라고도 불리고 있습니다.
채권은 어떤 종류가 있는가
1. 국채 : 발행체가 국가인 경우
2. 지방채 : 지방공공단체
3. 사채 : 민간기업
채권의 발행조건은 어떤 것인가
사채의 발행조건 예
발행총액 : 2,500억엔
각사채의 액면금액 : 1억엔
이율 : 연 0.4%
발행가격 : 각 사채의 액면금액 100엔에 붙는 금액 100엔
이자지급일 : 매년 4월 및 10월의 각 14일 (초회 이자지급일 : 2022년 4월 14일)
납부기한 : 2021년 10월 14일
상환기한 : 2031년 10월 14일
5.2 수익률과 가격은 어떻게 결정되는가
채권의 수익률이란
- [수익률]과 [이자율]의 차이
[이자율]이란, Coupon Rate(액면이자율)라고 불리며,
채권의 액면에 대해서 몇%의 이자가 붙는지 비율을 나타내는 것이다.
[수익률]이란, 투자원금에 대해서 1년 당 몇%의 수익을 얻을 수 있는지 나타내는 것이다.
그런데, 이자율은, 새로 정해진 조건에 변하는 것이 없는 한편, 수익율은, 채권의 가격변동에 따라서, 변화합니다.
채권 수익률 요소
채권 투자의 Return
- 이자수입 (Income Gain)
- 상환(매각) 시의 차손익 (Capital Gain or Capital Loss)
- [수익률]에도 종류가 있음
[직접 수익률]
이것은 채권 추자의 이자 수입(Income Gain)만을 고려한 이자 지급으로, [직리]라고도 한다.
직접수익률(%) = 이자수입(1년 당 Income Gain) / 구입가격

예를 들어, 연이율 5%의 채권을 90엔에 구입한 경우의 직접수익률는,
5 / 90 = 5.56%
[단리 최종 수익률]
이자수입(Income Gain)과 상환 시의 상환차손익(Capital Gain)을 고려한 이자가 단리최종수익률다.
단리최종수익률(%)
= [ 이자수입(1년 당 Income Gain) + { ( 액면 - 구입가격 ) / 잔존기간 }(1년 당 Capital Gain) ] / 구입가격

예를 들어, 연이율 5%, 구입가격 90엔, 잔존기간 10년의 채권을 만기까지 보유한 경우의 단리최종수익률은,
5 + { (100-90) / 10 } / 90 = 6.67%
[할인채 수익률]
할인채란, 이자수입이 없는 것으로, 구입가격이 액면금액보다 낮은 채권이다.
즉, 이자수입 대신에, 상환 시의 상환 차익(Capital Gain)을 얻는 채권이다.
할인채의 연수익률
<기간 1년 이내의 연수익률 ... 단리계산>
연수익률(%) = { ( 액면 - 구입가격 ) / 구입가격 } / 잔존기간
<기간 1년 초과의 연수익률 ... 복리계산>
연복리수익률(%) = 잔존기간 (루트) ( 액면가 / 구입가격 ) - 1

단리최종수익률의 문제점
・ 본래는 상환 시 및 매각 시에만 발생하는 상환차손익이나 매각차손익을,
매년 균등하게 받고 있는 것으로 가정
・ 돈의 시간 가치를 고려하지 않음.
즉, 1년 후에 받을 이자도, 2년 후에 받을 이자도 동일한 가치라고 가정하고 있음
채권가격은 어떻게 정해지나?
채권의 가격은, 그 채권이 발생하는 Cash Flow를 현재가치로 할인한 것의 합계다.
시장금리가 올라가면 채권가격은 내려가고,
시장금리가 내려가면 채권가격은 올라간다.
시장금리와 채권가격은 역의 움직임을 한다
시장금리 상승 → 채권금리 하락
시장금리 하락 → 채권금리 상승
- 복리최종수익률이란
채권의 가격은, 그 채권이 발생하는 Cash Flow를 현재가치로 할인한 것의 합계
① P = C(1) / ( 1 + YTM ) + C(2) / ( 1 + YTM )^2 + C(3) / ( 1 + YTM )^3 + ... + C(t) / ( 1 + YTM )^t
② -P + C(1) / ( 1 + YTM ) + C(2) / ( 1 + YTM )^2 + C(3) / ( 1 + YTM )^3 + ... + C(t) / ( 1 + YTM )^t = 0
NPV = - C(0) + C(1) / ( 1 + IRR ) + C(2) / ( 1 + IRR )^2 + C(3) / ( 1 + IRR )^3 + ... + C(t) / ( 1 + IRR )^t = 0
5.3 채권의 Risk
신용 Risk(Default Risk) - 발생체가 도산
가격변동 Risk - 금리변동에 따른 채권가격이 변동
유동성 Risk - 매각하고 싶을 때 매각할 수 없음
채권의 신용리스크와 등급
사채의 이율(Coupon Rate)는, TIBOR 등의 기준금리에 Spread를 가산하는 형태로 제시
BB이하의 투자부적격 종목은, High Yield채(고이자채), 또는 Junk Bonds라고 불림
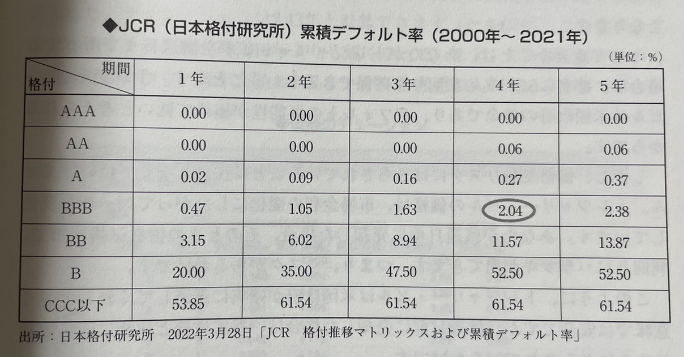
JCR(일본등급영구회) 누적 Default율 (2000년 ~ 2021년)
예를 들어, BBB의 등급의 회사가 4년 내 Default 할 확률은 2.04%
채권의 가격변동 Risk
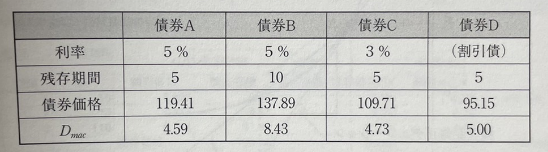
시장금리의 변동에 따른 채권가격의 감도를 나타내는 지표로 Duration이 있다.

먼저, 채권A와 채권B와 같이, 이자가 동일하면, 잔존기간이 짧을 수록, Duration이 짧음
채권A와 채권C와 같이, 잔존기간이 같으면, 이율이 높을 수록, Duration이 짧아짐
5.4 금리의 기간구조
Spot Rate로 채권가격을 구하다
미국에는, Zero Coupon채로 불리는 국채가 있다.
Zero Coupon채는 이름 그대로 채권의 발행일로부터 상환일까지는 Coupon(이자)의 지급은 전혀 없는 채권을 말한다.
일본에서는 할인채라고 하는 것이 이해하기 쉬울 수 있다.
Zero Coupon채에는 여러가지 기간이 있으나,
Cash Flow가 상환일에만 있는 것으로 Zero Coupon채의 가격에서 산출되는 복리최종이율은,
각각의 기간에 대응하는 이율에 상당한다.
이것을 이율을 Spot Rate이라고 한다.

실은 채권의 가격은 이 Spot Rate에 의해서 결정되는 것이다.

이 가격에서 역으로 복리최종이율을 구해보면, 이 채권의 복리최종이율은 6.76%로 계산된다.

① 여러가지 기간의 Zero Coupon채(할인채)의 복리최종금리(Spot Rate)를 계산하고,
② Spot Rate로부터 채권가격을 계산한다.
③ 그 채권가격에서, 복리최종이율을 구한다.
- Yield Curve는 우상향
여러가지 기간의 Zero Coupon채가 있는 경우, 그 복리최종이율인 Spot Rate는 기간에 의해 상이하다.
Spot Rate를 Plot한 것이 Yield Curve 라고 한다.
단기금리가 낮고 장기금리가 높은 우상향의 모향 (순 Yield)를 취하는 것이 일반적이다.
단, 장래에 있어서 경기의 감퇴가 생각되어, 금융완화를 향한 Timing에서는
단기금리가 높고, 장기금리가 낮은 우하향 모향 (역 Yield)가 되는 것도 있다.

이 Yield Curve에 표현되는 것과 같은 금리와 기간의 관계에 관한 이론을,
금리의 기간구조이론(Term Structure Theory)라고 한다.
그리고, Yield Curve의 모양을 설명하는 것으로서,
순수기대가설과 유동성 Premium가설, 그리고 시장분단가설의 3개의 가설이 있다.
[순수기대가설 (pure expectation hypothesis)]
Spot Rate가 현재에서 장래의 어느 시점 사이에 적용되는 금리인 것에 대해,
Forward Rate는 장래의 어느 2개의 시점의 사이에 적용되는 금리이다.
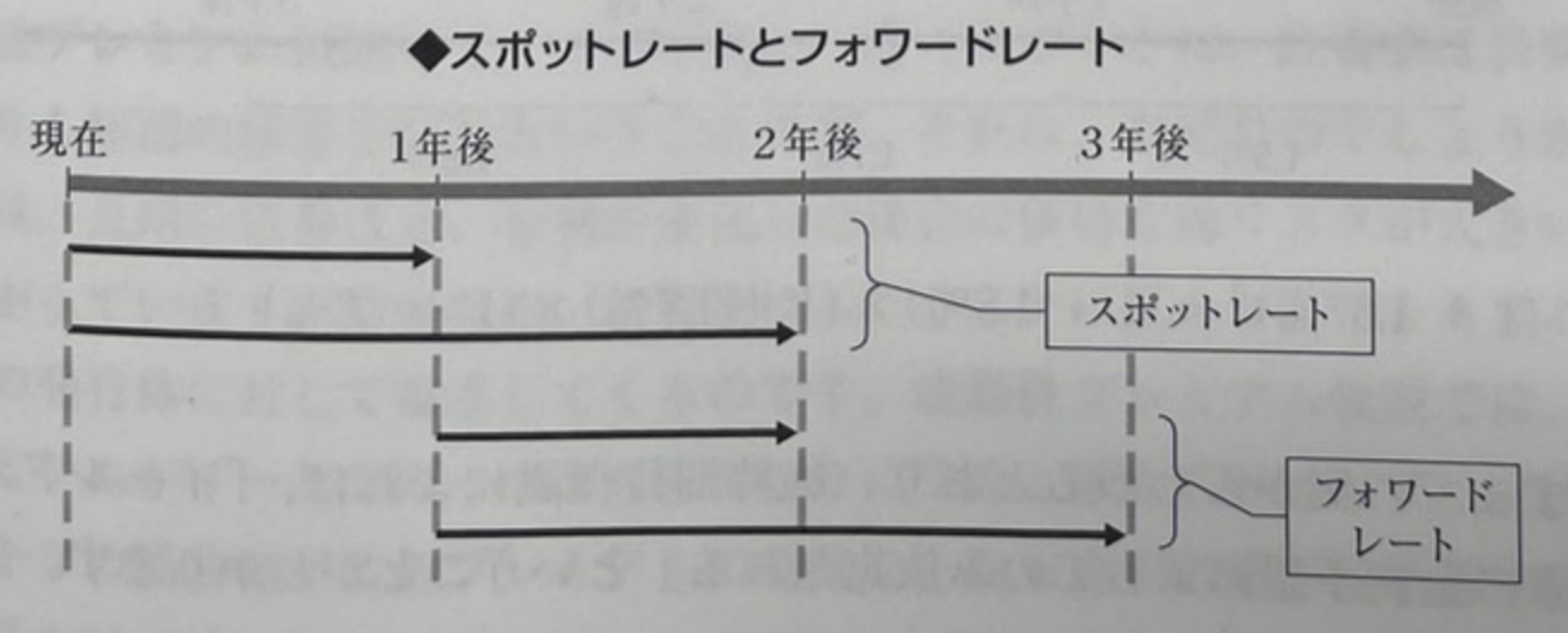
순수기대가설이란, 자기금리는 장래의 금리의 기대치로 결정되는 것이다.
따라서, Spot Rate와 Forward Rate와의 사이에는 다음과 같은 관계가 성립한다.

여기서 r(n)은 n기까지의 Spot Rate를 나타내고,
(n-1)f(n)은 n-1기에서 n기까지의 Forward Rate를 나타낸다.
순수기대가설의 전제
- 투자가는, 투자기간에 따른 Return을 최대로 하는 것에 흥미가 있어서,
단기운용이 좋거나, 장기운용이 좋거나 하는 선하고 있거나 하는 것은 아니다.
- Market은 효율적으로, 새로운 정보는 순식간에 Market에 반영된다.
- 투자가는 세금이나 거래 Cost가 발생하지 않고, 순식간에 거래를 행할 수 있다.
이런 전제가 성립되면, 앞선 식의 장기금리는, Spot Rate와 Forward Rate의 기하평균에 대등한 것을 알 수 있다.
3년물의 할인채로 운용한 경우의 수익률과,
1년물의 할인채로 3번 투자한 경우의 수익률이 같아지도록 금리재정이 발생한다.

순수기대가설에 의하면, [Yield Curve는 장래의 금리예상에 의해서만 결정된다]는 것을 알 수 있다.
단기의 금리가 상승할 것이라고 예상되면, 상기 식이 성립될 때까지, 장기금리도 상승한다는 것이다.
그 결과, Yield Curve는 상승해간다는 것이 된다.
- 역 Yield - 단기금리의 동향을 예상한다.
Yield Curve가 우하향하는 상태를 역 Yield라고 하나, 이것은 단기금리가 내려간다는 예상을 하는 것을 나타낸다.
이처럼 Yield Curve의 형태에 의해서,
단기금리가 향후 어떻게 될지 시장이 예상하고 있는지를 알 수 있다 는 것이다.
결국, 이 순수기대가설이 말하는 것은,
투자기간이 정해져있으면, 어떤 기간을 조합해서도 평균 Return은 바뀌지 않는다 라는 것이다.
기업이 자금조달을 행할 때, 단기차입으로 조달하여, 그것을 Roll Over(계속) 해가는 것과,
장기차입으로 조달해서도 결국, 지급 금리는 변하지 않는다는 것을 의미한다.
따라서, 장래의 금리를 예상하면서, [차입은 단기가 좋은지 장기가 좋은지]를 논의하는 것은 의미없다는 것이다.
[유동성 Premium 가설(Liquidity Premium Hypothesis)]
순수기대가설은, 어떤 의미로, 매우 엄격한 전제조건 상에 성립된다고 할 수 있다.
선술한 것과 같이, 투자가는 투자 Return의 최대화가 유일의 관심사라서,
단기던 장기던 운용기간의 선호는 없다고 가정하고 있다.
만약, 투자가가 선호가 있다고 한다면 어떨까?
여기서 등장하는 것이 유동성 Premium 가설이다.
이 가설의 첫번 째 Point는, 투자가는 장기의 채권보다 단기의 채권을 선호한다는 것이다.
실은 장기채일 수록 금리가 변화할 경우의 가격 변동 RISK가 크다는 걸 알 수 있다.
그 때문에, 투자가는 이 RISK에 합당한 Premium을 장기채의 발행체에 대해 요구해온다.
유동성 Premium 가설에서는, 이 Premium이 Yield Curve를 우상향한다고 생각하는 것이다.
역 Yield Curve의 경우는, 이 Premium의 효과를 상회하는 금리의 저하를 예상하는 요인이 있는 것이다.
또한, 투자가가 장기의 채권에 투자하는 경우는, 자금이 장기에 걸쳐서 고정되어버려, 자유롭게 쓸 수 없어진다.
따라서, 장기의 채권에 투자 받기 위해서는,
발행체는 순수기대가설에서 계산되는 수익율보다도 높은 수익율을 제공할 필요가 있는 것이다.
이 유동성 Premium 가설이 맞다고 생각하면, 우상향의 Yield Curve라고 해서,
[장래, 단기금리가 상승한다]라고 시장이 생각하고 있다는 것은 되지 않는다.
자금조달 Cost는 장기가 되면 될 수록 높기 때문에, 단기로 차입을 하는 것에 의해, Cost를 낮출 수 있다.
물론, 그 기업이 장기에 걸쳐서 용이하게 차입을 할 수 있는 우량기업인 것이 전제조건이다.
[시장분단가설 (Segmented Market Hypothesis)]
채권시장은, 만기일까지의 기간에 의해 분단되어있다는 생각이다.
따라서, 순수기대가설에 논하고 있는 듯이, 단기금리와 장기금리와의 사이에서 재정이 발생한다는 것도 없다.
각각의 기간의 금리는, 어디까지나 Market에서의 수요관계에 의해서 결정된다고 생각되는 것이다.
5.5 주식의 기초
주식회사 - 주식을 발행하는 것으로, 다수의 투자가로부터 사업자급을 모아, 그것을 원금으로 사업활동을 진행하여,
이익을 높히는 것을 목적으로 하는 회사
주주 - 주식회사에 자금을 출자하는 사람
주가의 거짓과 진실
주가 = 주식시가총액 / 발행주식수
발행주식수를 제외하고 주가가 높다 낮다라고 하는 것은 옳지 않다.
주가는 어떻게 정해지나?
1. 기업의 업적이나 장래성과는 무관계로 시장 참가자의 심리의 상승(相乗, 시너지)으로 형성되어있음
케인즈는 주식투자는 미인콘테스트와 같아,
어떤 종목의 주가가 상승하는 것은, 시장 참가자가, [주가가 오른다]라고 생각하기 떄문이며,
기업의 장래성이나 수익성과는 관계가 없다라고 함
2. 기업의 장래성이나 수익력을 반영함
주가의 결정이론
주가란
주가 = 장래 배당을 주주자본 Cost로 현재가치로 할인한 것의 합계
P(0) = Div(1) / (1+r) + Div(2) / (1+r)^2 + Div(3) / (1+r)^3 + ... + Div(t) / (1+r)^t + P(t) / (1+r)^t
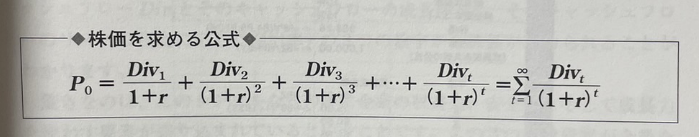
배당할인모델 (DDM, Dividend Discounted Model)
주가란 장래에 걸쳐 주주가 얻는 Cash Flow인 배당을
투자가의 요구(기대)수익률인 주주자본 Cost로 할인한 현재가치의 합계
배당에서 이론주가를 구하다
주가를 구하는 계산식
P = Div(1) / ( r(E) - g )
r(E) : 주주자본 Cost
g : 배당성장률
- 채권이란 발행 시에 정해진 조건에 따라서, 정기적으로 일정의 이자를 지급하여,
만기일에 액면 전체를 상환(반제)하는 것을 발행체가 약속하고 있는 증권이다. - 채권의 [이자율]이란, 채권의 액면에 대하여 몇%의 이자가 붙는지에 대한 비율을 표시하는 것으로
상환될 때까지 변하는 것은 없다.
한편, [수익률]은, 투자원금(구입가격)에 대하여,
1년 당 몇%의 Cash Flow를 얻을 수 있는지를 나타내는 것으로,
수익률은 채권의 가격(구입가격)에 따라서 변화한다. - 채권의 가격은 그 채권이 발생하는 Cash Flow의 현재가치의 합계이다.
따라서, 시장금리(할인율)이 올라가면 채권가격은 내려가고,
시장금리가 내려가면 채권가격은 올라가는 관계가 있다. - 채권 투자는, 발행체가 도산한다는 신용 Risk와,
시장금래의 변화에 따라 발생하는 가격변동 Risk,
또한, 매매가 극단적으로 적게되는 것으로 거래가 성립하지 않고,
매매하고 싶을 때 할 수 없는 유동성 Risk 등이 있다. - 시장금리의 변화에 따른 채권가격의 감도를 나타내는 지표가 Duration이다.
따한, 금리가 1% 변화할 때 채권가격이 몇% 변화하는지를 나타내는 것이 수정 Duration 이다. - 각 기간과 그것에 대응하는 금리와의 관계를 나타내는 Graph를 Yield Curve라고 한다.
단기 금리가 낮고 장기금리가 높은 우상향형 (순 Yield)가 되는 것이 일반적이다.
한편, 마크로 환경에 있어서는, 단기금리가 오르고, 장기금리가 낮은 우하향(역 Yield)가 되는 경우도 있다. - 금리와 기간의 관계에 관한 이론을 금리의 기간구조이론이라고 하며, Yield Curve의 형태를 설명하는 가설로서,
순수기대가설과 유동성 Premium가설, 그리고 시장분단가설의 3가지가 있다. - 배당할인모델 (DDM : Dividend Discounted Model)이란,
[주가는 주주가 얻는 배당을 주주자본 Cost로 할인한 현재가치의 합계이다] 라는 생각 방식을 말한다.
(Finance) 도구로서의 파이낸스 제6장 Derivatives의 이론과 실전적 지식
6.5 Option이란 Option은 [보험] Option은 Derivatives 거래의 대표선수라고 말할 수 있을지 모릅니다. 간단히 말하면, Option은 [보험]입니다. 보험은 RISK에 대한 Hedge(회피) 수단인 것입니다. Option의 경우는,
fastcho.tistory.com
'WBS - 2023 Spring > Finance' 카테고리의 다른 글
| (Finance) 도구로서의 파이낸스 | 제2장 증권투자에 관한 이론 (0) | 2023.05.09 |
|---|---|
| (Finance #7-8) 가준평균자본 Cost (WACC) 와 정리 (0) | 2023.05.08 |
| (Finance) 도구로서의 파이낸스 | 제3장 기업가치평가 (0) | 2023.05.02 |
| (Finance #5-6) Free Cash Flow와 주식(기업가치)의 평가 (0) | 2023.05.01 |
| (Finance #3-4) 프로젝트의 평가-정미현재가치(NPV)와 내부수익률(IRR) | 채권가격의 평가와 이자 (0) | 2023.04.23 |
| (Finance) 도구로서의 파이낸스 | 제1장 투자에 관한 이론 (0) | 2023.04.20 |
| (Finance #3-4) 로그 log 설명자료 (0) | 2023.04.19 |
| (Finance #1-2) 파이낸스 ファイナンス(夜間主)| HIBARA Nobuhiko 樋原 伸彦 | Waseda Business School | 와세다 MBA (0) | 2023.04.18 |



